论文阅读 | Augmenting Neural Networks with First-order Logic
论文地址: https://arxiv.org/abs/1906.06298
研究的问题:
已有研究工作:
神经网络训练的主流方法是在大型数据集上最小化任务损失,但是它需要大量的训练集,比如训练一个翻译模型需要大量对应的句子对,对于有注释的数据就很难使用。比如下面这个例子。

以往的研究是需要通过改变训练方法来加入逻辑知识的。
本文的工作和创新点:
本文要做的是希望在不改变端到端的训练方法的前提下,用一阶逻辑表示知识,将这些结构化的知识整合到神经网络的架构当中。
研究方法:
本文主要围绕下面三个问题展开:
1、我们能否将声明性的规则和端到端网络的训练结合起来?
2、这些规则是否可以帮助缓解对数据的需求?
3、如何结合将预训练的表示和领域内的专业知识结合起来?
首先是如何将约束条件加到现有的神经网络中,方法是通过扩展现有网络的计算图,增加由约束定义的边。对于原神经网络y=g(Wx),其中g作为激活函数,W为参数,x、y为输入输出,计算被拓展为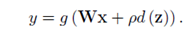
其中d为距离函数,它是一个可微的函数,并且体现了约束条件是否为真,p作为超参数存在。
问题就转为为,寻找合适的距离函数。一个理想的距离函数应当是这样的:

但是它是不可微的。本文用的是Lukasiewicz T-norm来定义的,具体如下:

实验部分:
本文在机器理解、自然语言理解、组块分析三个任务上展开了实验,主要的目标是研究在低数据的状态下,这样的增强网络如果实施及其效果。
下面以组块分析(text chunking)为例介绍。
关于谓词的定义如下:

它们的依赖关系如下:
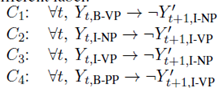
上述规则也可以在输出空间中,以硬约束的形式应有,本框架的优势在于提供了一种可微分的方式在训练和预测期间监督模型。
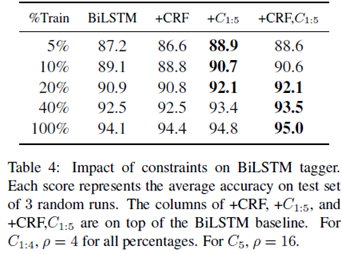
实验结果如下:
评价:
本文主要做的利用结构化的一阶逻辑式,如布尔逻辑,在不改变端到端训练方法的前提下,改进训练效果。这里主要的问题包括,一阶逻辑式本身不可微,存在环等,通过引入Łukasiewicz T-norm解决,这里不是很了解。不过从实验结果上看,在低数据的情况下提升还是比较明显的。



