[收藏]统计中的置信和惩罚

http://www.zhizhihu.com/html/y2013/4151.html

 

如何对样本数目加惩罚来保证置信，样本数目很少的时候，统计结果往往不置信。

看了阮一峰老师的博客和《How Not To Sort By Average Rating》，还有论文《How to Count Thumb-Ups and Thumb-Downs》，还有wiki上的各种置信区间《confidence interval》，了解了一些方法，例如：

一、威尔逊置信区间（Score = Lower bound of Wilson score confidence interval for a Bernoulli parameter）：

1927年，美国数学家 Edwin Bidwell Wilson提出了一个修正公式，被称为"威尔逊区间"，很好的解决了这个问题。基于威尔逊区间的置信区间计算公式如下：

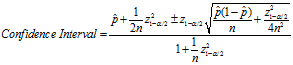
上述公式中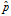，表示某一话题的"赞成票比例"，n表示样本大小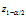，表示对应某个置信水平的z统计量，这是一个常量，可以通过查表得到。一般情况下，在85%和95%的置信水平下z统计值分别为1.0和1.6。

威尔逊置信区间的下限值为：

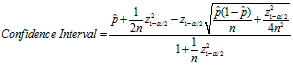
可以看到，当n的值足够大时，这个下限值会趋向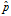。如果n非常小（投票人很少），这个下限值会大大小于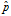。实际上，起到了降低"赞成票比例"的作用，使得该项目的得分变小、排名下降。

这就是目前Reddit评论使用的主要排名算法。

帮助

01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18

cpdef double _confidence(int ups, int downs): """The confidence sort.   http://www.evanmiller.org/how-not-to-sort-by-average-rating.html"""   cdef float n = ups + downs   if n == 0: return 0   cdef float z = 1.281551565545 # 80% confidence cdef float p = float(ups) / n   left = p + 1/(2*n)*z*z right = z*sqrt(p*(1-p)/n + z*z/(4*n*n)) under = 1+1/n*z*z   return (left - right) / under

二、贝叶斯平均：

除了威尔逊区间法之外，贝叶斯平均法【11】也非常适合于解决与时间无关的排序问题。威尔逊区间法很好地解决了投票人数过少、导致结果不可信的问题，但同时也存在一个致命问题，即马太效应：排行榜前列总是那些票数最多的项目，新项目或者冷门项目，很难有出头机会，排名可能会长期靠后。

举例来说，一部好莱坞大片有10000个观众投票，一部小成本的文艺片只有100个观众投票。这两者的投票结果，怎么比较？如果使用"威尔逊区间"，后者的得分将被大幅拉低，这样处理是否公平，能不能反映它们真正的质量？一个合理的思路是，如果要比较两部电影的好坏，至少应该请同样多的观众观看和评分。既然文艺片的观众人数偏少，那么应该设法为它增加一些观众。

基于这个思路，IMDB数据库在其网站的电影推荐功能中提出了贝叶斯平均法进行排序。具体计算公式如下：

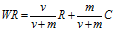
其中，

- WR， 加权得分（weighted rating）

- R，该电影的用户投票的平均得分（Rating）

- v，该电影的投票人数（votes）

- m，排名前250名的电影的最低投票数（现在为3000）

- C， 所有电影的平均得分（现在为6.9）

仔细研究这个公式，我们会发现，IMDB为每部电影增加了3000张选票，并且这些选票的评分都为6.9。这样做的原因是，假设所有电影都至少有3000张选票，那么就都具备了进入前250名的评选条件；然后假设这3000张选票的评分是所有电影的平均得分（即假设这部电影具有平均水准）；最后，用现有的观众投票进行修正，长期来看，v/(v+m)这部分的权重将越来越大，得分将慢慢接近真实情况。

这样做拉近了不同电影之间投票人数的差异，使得投票人数较少的电影也有可能排名前列。

把这个公式写成更一般的形式：

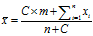
其中，

- C，投票人数扩展的规模，是一个自行设定的常数，与整个网站的总体用户人数有关，可以等于每个项目的平均投票数

- n，该项目的现有投票人数

- x，该项目的每张选票的值

- m，总体平均分，即整个网站所有选票的算术平均值

这种算法被称为"贝叶斯平均"（Bayesian average）。因为某种程度上，它借鉴了"贝叶斯推断"（Bayesian inference）的思想：既然不知道投票结果，那就先估计一个值，然后不断用新的信息修正，使得它越来越接近正确的值。