机器学习【三】k-近邻(kNN)算法
一、kNN算法概述
kNN算法是用来分类的,其依据测量不同特征值之间的距离,其核心思想在于用距离目标最近的k个样本数据的分类来代表目标的分类(这k个样本数据和目标数据最为相似)。其精度高,对异常值不敏感,并且无数据输入假定,但是计算复杂度和空间复杂度均高,更多的适用于数值型和标称型数据。
kNN算法的工作原理:存在一个训练样本集,并且其中的每个数据都存在标签,因此样本集中的数据与其所属分类的对应关系是明确的。输入没有标签的新数据后,提取新数据中的特征并与样本集中数据对应的特征进行比较,然后算法提取样本集中特征最相似数据(最近邻)的分类标签。找到最相似的k个数据,这k个数据出席那次数最多的分类,即输入的具有特征值的数据的分类。k通常是不大于20的整数。
举例说明:
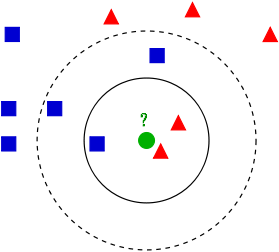
训练样本集中包含一系列数据,这个数据包括样本空间位置(特征)和分类信息(即标签,属于红色三角形还是蓝色正方形),要对中心的绿色数据的分类。运用kNN算法思想,距离最近的k个样本的分类来代表测试数据的分类,那么:
当k=3时,距离最近的3个样本在实线内,具有2个红色三角和1个蓝色正方形,因此将它归为红色三角形。
当k=5时,距离最近的5个样本在虚线内,具有2个红色三角和3个蓝色正方形,因此将它归为蓝色正方形。
二、k-近邻算法的一般流程
一般情况下,kNN有如下流程:
(1)收集数据:确定训练样本集合测试数据;
(2)计算测试数据和训练样本集中每个样本数据的距离;
常用的距离计算公式:

(3)按照距离递增的顺序排序;
(4)选取距离最近的k个点;
(5)确定这k个点中分类信息的频率;
(6)返回前k个点中出现频率最高的分类,作为当前测试数据的分类。
三、Python算法实现
建立一个Knn.py文件对算法进行验证实现
首先在Knn.py中定义一个生成“训练样本集”的函数:
#定义一个生成“训练样本集”的函数,并给出训练数据以及对应的类别
from numpy import *;
import operator;
def creatDataSet():
group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
labels = ['A','A','B','B']
return group, labels
然后建立一个kNN算法分类器,实施kNN算法
#定义KNN算法分类器函数
#函数参数包括:(输入向量inX,训练数据dataSet,标签向量labels,最近邻居数k值)
def classfiy (inX,dataSet,labels,k):
dataSetSize = dataSet.shape[0]
# 计算欧式距离
diffMat = tile(inX,(dataSetSize,1)) - dataSet
sqDiffMat = diffMat ** 2
sqDistances = sqDiffMat.sum(axis=1) #行向量分别相加,从而得到新的一个行向量
distances = sqDistances ** 0.5
# 排序
sortedDistIndicies = distances.argsort() #排序并返回index
# 选择距离最近的k个值
classCount = {}
for i in range(k):
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
#排序
sortedClassCount = sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]
使用欧式距离计算两个向量点之间的距离,计算完所有点之间的距离之后,对数据进行从小到大排序,然后确定前k个距离最小元素所在的主要分类。最后将classCount字典分解为元组列表,然后使用程序第二行导入的运算符模块的itemgetter方法,按照第二个元素的次序对元组进行排序。此处为逆序,最终返回频率最高的标签。
在cmd下测试预测结果
>>>import Knn #生成训练样本 >>>group,labels=KNN.createDataSet() #对测试数据[0,0]进行KNN算法分类测试 >>>KNN.classify([0,0],group,labels,3) Out[3]: 'B'
四、示例
1.kNN算法改进约会网站的配对效果
这个示例用于使用kNN算法做出推荐。首先数据样本包含三个特征,(a)每年获得的飞行常客里程数(b)玩游戏消耗的时间(c)每周消耗的冰激淋公升数
分类数据(是否喜欢(1表示不喜欢,2表示魅力一般,3表示极具魅力))
(1)准备数据:将文本记录转换为Numpy
文件为1000行4列的数据,每行包含3行特征数据和1行分类数据
def file2matrix(filename):
fr = open(filename) #读取文件
arrayOlines = fr.readline() #按行读取
numberOfLines = len(arrayOlines) #得到文件行数
returnMat = zeros((numberOfLines,3))#生成3阶全0矩阵,用于返回
classLabelVector = []
index = 0
#解析文件数据到列表
for line in arrayOlines:
line.strip()
listFromLine = line.split('\t')
returnMat[index,:] = listFromLine[0:3]#得到特征变量
classLabelVector.append(int(listFromLine[-1]))#得到目标分类变量
index += 1
return returnMat,classLabelVector
截取前三个元素,并将其存储到特征矩阵中;利用负索引,可以获取最后一列的元素。现在已经从文本中导入了数据,并将其格式化为想要的数据,接下来以图形的方式可视化数据。
(2)分析数据:使用Matplotlib创建散点图
散点图使用datingDataMat矩阵的第二、三列数据绘制得到
##datingDataMat,datingLabels = Knn.file2matrix('datingTestSet.txt')
import matplotlib
import matplotlib.pyplot as plt
#对第二列和第三列数据进行分析:
fig=plt.figure()
ax=fig.add_subplot(111)
ax.scatter(datingDataMat[:,1],datingDataMat[:,2],c=datingLabels)
plt.xlabel('Percentage of Time Spent Playing Video Games')
plt.ylabel('Liters of Ice Cream Consumed Per Week')
在图中,一般采用色彩或者其他记号来标记不同样本分类,以便来理解数据
(3)准备数据:归一化数据
由于在方程中不同的数据在大小上差别较大,在计算欧式距离,整体较大的数据所占的比重明显更高,因此需要对数据进行归一化处理。如将取值范围处理为0到1或者-1到1之间。通常采用如下公式,将任意范围的特征值转化为0-1之间:
newValue = (oldValue-min) / (max-min)
##归一化特征值
def autoNorm(dataSet):
minVals = dataSet.min(0) #最大值
maxVals = dataSet.max(0) #最小值
ranges = maxVals - minVals
normDataSet = zeros(shape(dataSet))#构建零矩阵
m = dataSet.shape[0] #行数,shape返回[nrow,ncol]
normDataSet = dataSet - tile(minVals,(m,1))#tile复制minval
normDataSet = normDataSet / tile(ranges,(m,1))#特征值相除,不是矩阵除法
return normDataSet,ranges,minVals
dataSet.min(0)中的参数0使得函数可以从列中选取最小值。同时使用Numpy库中的tile()函数将变量内容复制成输入矩阵同样大小的矩阵。
然后在Python命令提示符下,重新加载Knn.py模块,执行autoNorm函数,检测函数的执行结果:
reload(KNN)
Out[145]: <module 'KNN' from 'G:\\Workspaces\\MachineLearning\\KNN.py'>
normMat,ranges,minVals=KNN.autoNorm(datingDataMat)
normMat
Out[147]:
array([[ 0.44832535, 0.39805139, 0.56233353],
[ 0.15873259, 0.34195467, 0.98724416],
[ 0.28542943, 0.06892523, 0.47449629],
...,
[ 0.29115949, 0.50910294, 0.51079493],
[ 0.52711097, 0.43665451, 0.4290048 ],
[ 0.47940793, 0.3768091 , 0.78571804]])
ranges
Out[148]: array([ 9.12730000e+04, 2.09193490e+01, 1.69436100e+00])
minVals
Out[149]: array([ 0. , 0. , 0.001156])
(4)测试算法:验证分类器
通常采用已有数据的90%作为训练样本来训练分类器,而用剩下的10%测试分类器效果。这里用错误率来检测分类器的性能。
#分类器测试代码
def datingClassTest():
hoRatio= 0.10 #测试数据的比例
datingDataMat,datingLabels=file2matrix('文件路径') #准备数据
normMat,ranges,minVals=autoNorm(datingDataMat) #归一化处理
m=normMat.shape[0] #得到行数
numTestVecs=int(m*hoRatio) #测试数据行数
errorCount=0.0 #定义变量来存储错误分类数
for i in range(numTestVecs):
classifierResult=classify(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)
print('the classifier came back with: %d,the real answer is: %d'%(int(classifierResult),int(datingLabels[i])))
if (classifierResult!=datingLabels[i]): errorCount+=1
print('the total error rate is : %f'%(errorCount/float(numTestVecs)))
测试代码中使用了file2matrix()和autoNorm()函数从文件中读取数据并将其转换为归一化特征值。接着计算测试向量的个数,这一步将一部分数据划分为测试集,一部分为训练集,然后将两部分数据输入原始分类器classify()中。最后计算错误率并输出。
(5)构建完整推荐系统
def classifypersion():
resultList=['not at all','in small doses','in large doses']
percentTats=float(input('percentage of time spent playing video games?')) #录入数据
ffMiles=float(input('frequent flier miles earned per year?'))
iceCream=float(input('liters of ice creamconsued per year?'))
datingDataMat,datingLabels =file2matrix('test.txt')
normMat,ranges,minVals=autoNorm(datingDataMat)
inArr=array([ffMiles,percentTats,iceCream])
classifierResult=classify((inArr-minVals/ranges),normMat,datingLabels,3)
print('You will probably like this persion :%s'%resultList[int(classifierResult)-1])
raw_input()函数是允许用户输入文本命令,并返回用户所输入的命令。
2.手写识别系统
(1)准备数据:将图像转换为测试向量
该函数创建1*1024的Numpy数组,然后打开给定文件,循环读出文件前32行,并将每行头32个字符值存储在Numpy数组中,最后返回数组。
def img2vector(filename):
returnvect=zeros((1,1024))
fr=open(filename)
for i in range(32):
lineStr=fr.readline()
for j in range(32):
returnvect[0,32*i+j]=int(lineStr[j])
return returnvect
(2)测试算法:识别手写数字
#手写数字识别系统
from os import listdir#列出给定目录的文件名
def handwritingClassTest():
hwLabels=[]
trainingFileList=listdir('文件名')#获取文件中的目录
m=len(trainingFileList) #得到文件数目
trainMat=zeros((m,1024))
#从文件名中解析分类数字
for i in range(m):
fileNameStr=trainingFileList[i]
fileStr=fileNameStr.split('.')[0]
classNumber=int(fileStr.split('_')[0])
hwLabels.append(classNumber)
trainMat[i]=img2vector('trainingDigits'%fileNameStr)
testFileList=listdir('testDigits')
errorCount=0
#解析测试数据的分类信息
mTest=len(testFileList)
for i in range(mTest):
fileNameStr=testFileList[i]
fileStr=fileNameStr.split('.')[0]
classNumber=int(fileStr.split('_')[0])
vectorUnderTest=img2vector('testDigits/%s'%fileNameStr)
classifierResult=classify(vectorUnderTest,trainMat,hwLabels,3)
print('the classifier came back with :%d,the real answer is:%d'%(classifierResult,classNumber))
if(classifierResult!=classNumber):errorCount+=1
print('\n the total number of errors is: %d'%errorCount)
print('\n total error rate is %f'%(errorCount/float(mTest)))
将trainingDigits目录中的文件内容存储在列表中,然后可以得到目录中的文件数量,并将其存入m中。再创建一个m行1024列的训练矩阵,该矩阵的每行数据存储一个图像。可以从文件名中解析出分类数字。
改变变量k的值、修改函数handwritingClassTest随机选取训练样本、改变训练样本的数目,都会对k-近邻算法的错误率产生影响。



