Learning Query and Document Similarities from Click-through Bipartite Graph with Metadata
读了一篇paper,MSRA的Wei Wu的一篇《Learning Query and Document Similarities from Click-through Bipartite Graph with Metadata》。是关于Ranking Relevence方面的文章。下面简单讲下我对这篇文章的理解,对这方面感兴趣的小伙伴们可以交流一下。
1. Abstract
这篇文章的重点在于使用query-doc的点击二部图,结合query/doc的meta数据(组织成multiple types of features),来学习出query-doc(顺带介绍了query-query,doc-doc)的similarity。
为了计算上述的similarity,作者采用了两个不同的linear mappings,用来把query从query feature space,把doc从doc feature space映射到相同的latent space上,然后便可通过计算这个latent space上两者的vector的dot product来获得两者的similarity。于是,便把对similarity的learning形式化为对mapping的learning,而这个mapping的learning的目标是为了maximize从enriched click-through bipartite gragh上观察到的query-doc的similarity(可以通过query-doc pair的点击数来衡量)。另外,这个linear mapping是针对一种类型的features,获得一种类型features的similarity function,如果有multiple types of features的话,则最终的similarity function是每个type的similarity function的线性组合。
learning过程用到的算法包括Singular Value Decomposition(SVD)和Multi-view Partial Least Squares(M-PLS)。
2. Introduction
作者提到了先前的关于计算query-doc similarity的几种方法。
1)feature based methods:Vector Space Model(VSM),BM25,Language Models for Information Retrieval(LMIR)等。
2)gragh based methods:mining query-doc similarity from a click-through bipartite gragh等。
而这篇文章是将两者结合起来:
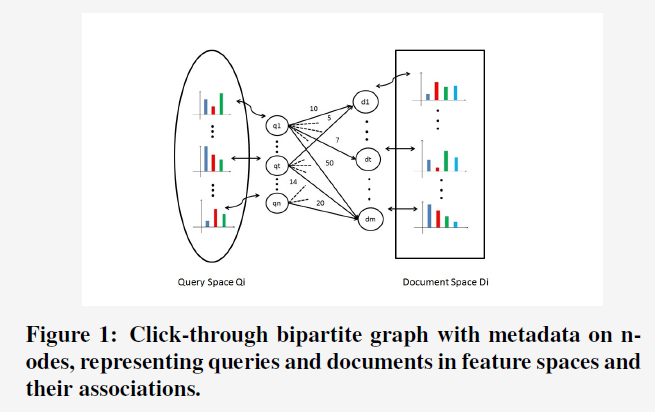
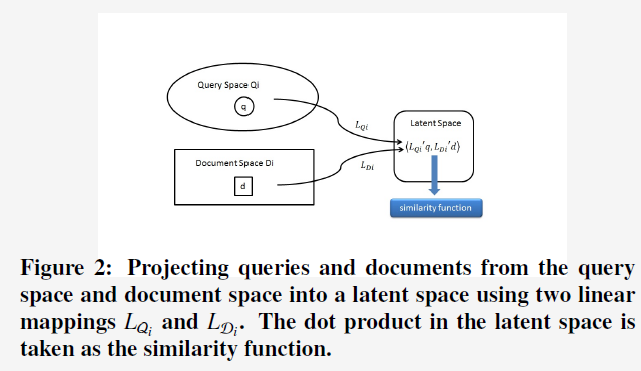
3. Problem Formulation
将每种type的features的query或者document用一个向量的形式来表示,,则linear mapping可以看做是维度为![]() 和
和![]() 的两种形式的矩阵(
的两种形式的矩阵(![]() 和
和![]() ),通过这两种变换矩阵,query或者doc在原始空间上的向量被变换成latent space上的维度为
),通过这两种变换矩阵,query或者doc在原始空间上的向量被变换成latent space上的维度为 的向量
的向量![]() 和
和![]() 。于是,对于这种type的faetures,simialrity function表示为
。于是,对于这种type的faetures,simialrity function表示为![]() 。我们可以将点击二部图中query-doc的点击数看作是query-doc similarity的大小,而通过maximize观察到的query-doc的similarity来学习linear mapping
。我们可以将点击二部图中query-doc的点击数看作是query-doc similarity的大小,而通过maximize观察到的query-doc的similarity来学习linear mapping![]() 和线性加权的权重
和线性加权的权重![]() 。
。
最终的learning problem可以表示为:
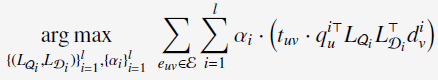
这时候有个问题,就是需要最大化的公式的值是可以无限大的,因为没有系数的限制,下面会介绍如何在系数上加上constraints。
4. Multi-view Partial Least Squares
4.1 Constrained Optimization Problem
1)对feature vectors进行归一化:![]() ,
,![]()
2)对mapping matrices![]() 进行正交化限制。
进行正交化限制。
3)对线性加权权重![]() 进行L2 正则化限制。
进行L2 正则化限制。
于是,learning method重新形式化为:
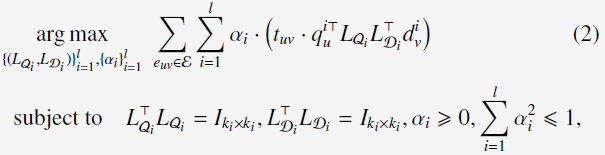
4.2 Globally Optimal Solution
为了获得全局最优解,两步走。第一步,对每种type的features,通过SVD求解得到optimal linear mapping;第二步,求解optimal combination weights。
上述的公式(2)可以重写为:
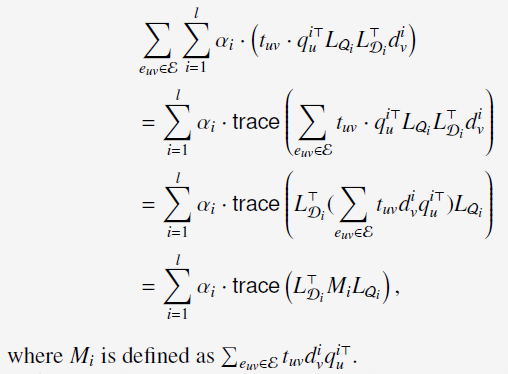
optimization problem为:
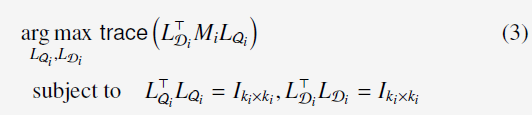
通过SVD求得global optimal solution。

于是,公式(2)可以写成:
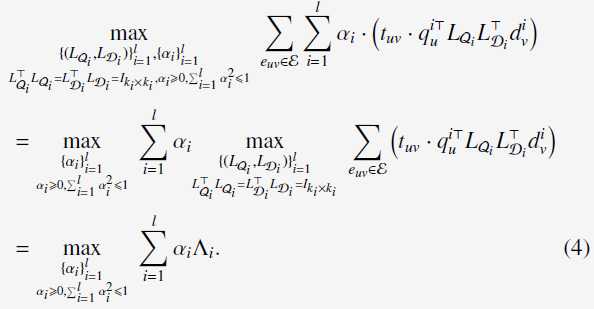
而combination weights求解为:
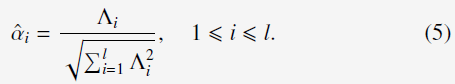
4.3 Learning Algorithm
1)for each type of feature,solves SVD of Mi to learn the linear mapping。
2)calculates the combination weights using (5)。

版权声明:
本文由笨兔勿应所有,发布于http://www.cnblogs.com/bentuwuying。如果转载,请注明出处,在未经作者同意下将本文用于商业用途,将追究其法律责任。



