LSA,pLSA原理及其代码实现
一. LSA
1. LSA原理
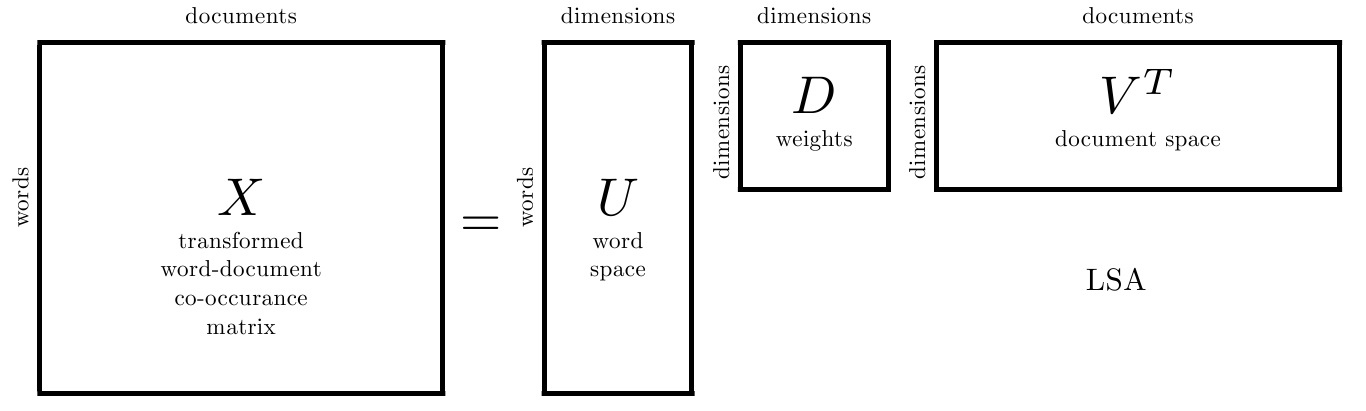
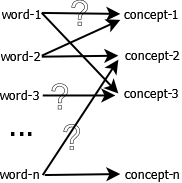
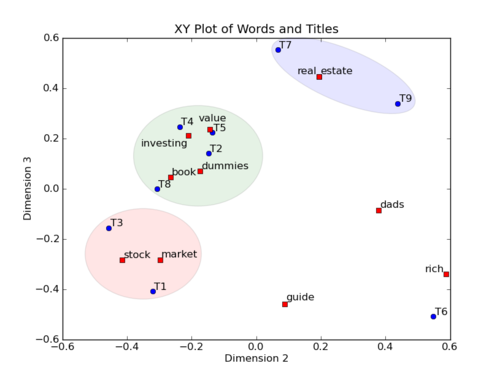
2. LSA的优点
3. LSA的缺点
二. pLSA
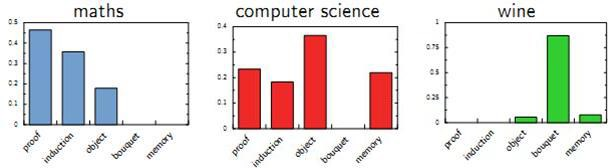
pLSA的建模思路分为两种。
1. 第一种思路
以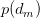 的概率从文档集合
的概率从文档集合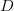 中选择一个文档
中选择一个文档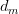
以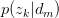 的概率从主题集合
的概率从主题集合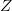 中选择一个主题
中选择一个主题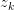
以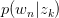 的概率从词集
的概率从词集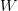 中选择一个词
中选择一个词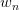
有几点说明:
- 以上变量有两种状态:observed (
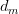 &
&  ) 和 latent (
) 和 latent (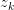 )
)  来自文档,但同时是集合(元素不重复),相当于一个词汇表
来自文档,但同时是集合(元素不重复),相当于一个词汇表
直接的,针对observed variables做建立likelihood function:
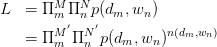
其中,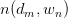 为
为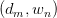 pair出现的次数。为加以区分,之后使用
pair出现的次数。为加以区分,之后使用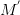 与
与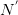 标识对应文档与词汇数量。两边取
标识对应文档与词汇数量。两边取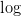 ,得:
,得:
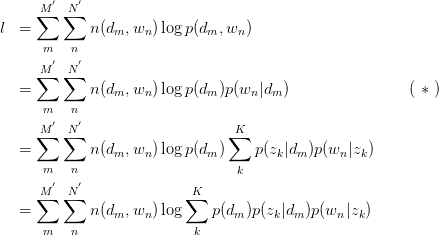
其中,倒数第二步旨在将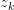 暴露出来。由于likelihood function中
暴露出来。由于likelihood function中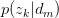 与
与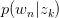 存在latent variable,难以直接使用MLE求解,很自然想到用E-M算法求解。E-M算法主要分为Expectation与Maximization两步。
存在latent variable,难以直接使用MLE求解,很自然想到用E-M算法求解。E-M算法主要分为Expectation与Maximization两步。
假设已知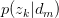 与
与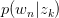 ,求latent variable
,求latent variable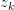 的后验概率
的后验概率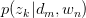
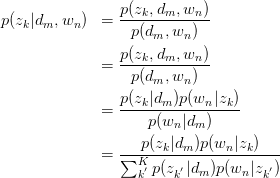
Step 2: Maximization
求关于参数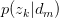 和
和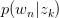 的Complete data对数似然函数期望的极大值,得到最优解。带入E步迭代循环。
的Complete data对数似然函数期望的极大值,得到最优解。带入E步迭代循环。
由 式可得:
式可得:
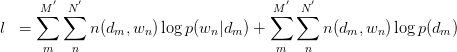
此式后部分为常量。故令:
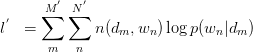
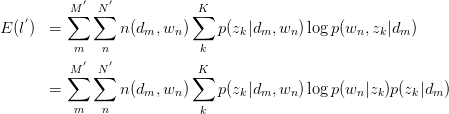
建立以下目标函数与约束条件:
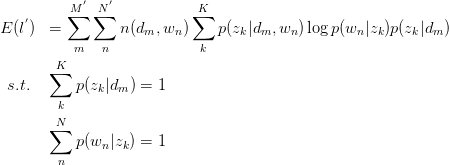
只有等式约束,使用Lagrange乘子法解决:
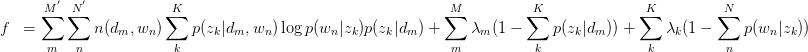
对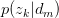 与
与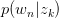 求驻点,得:
求驻点,得:
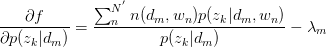
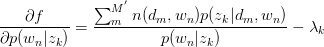
令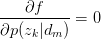 ,得:
,得:
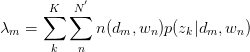 ,故有:
,故有:
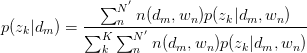
同理,有:
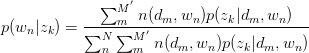
将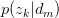 与
与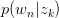 回代Expectation:
回代Expectation:
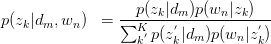 ,循环迭代。
,循环迭代。
pLSA的建模思想较为简单,对于observed variables建立likelihood function,将latent variable暴露出来,并使用E-M算法求解。其中M步的标准做法是引入Lagrange乘子求解后回代到E步。
总结一下使用EM算法求解pLSA的基本实现方法:
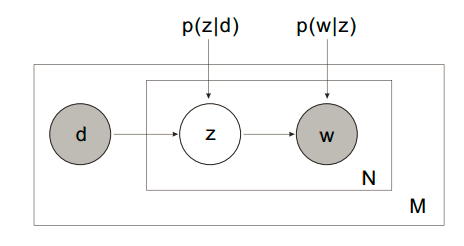
2. 第二种思路
这个思路和上面思路的区别就在于对P(d,w)的展开公式使用的不同,思路二使用的是3个概率来展开的,如下:
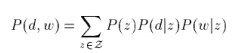
这样子我们后面的EM算法的大致思路都是相同的,就是表达形式变化了,最后得到的EM步骤的更新公式也变化了。当然,思路二得到的是3个参数的更新公式。如下:

你会发现,其实多了一个参数是P(z),参数P(d|z)变化了(之前是P(z|d)),然后P(w|z)是不变的,计算公式也相同。
给定一个文档d,我们可以将其分类到一些主题词类别下。
PLSA算法可以通过训练样本的学习得到三个概率,而对于一个测试样本,其中P(w|z)概率是不变的,但是P(z)和P(d|z)都是需要重新更新的,我们也可以使用上面的EM算法,假如测试样本d的数据,我们可以得到新学习的P(z)和P(d|z)参数。这样我们就可以计算:
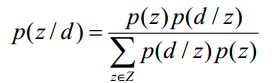
为什么要计算P(z|d)呢?因为给定了一个测试样本d,要判断它是属于那些主题的,我们就需要计算P(z|d),就是给定d,其在主题z下成立的概率是多少,不就是要计算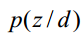 吗。这样我们就可以计算文档d在所有主题下的概率了。
吗。这样我们就可以计算文档d在所有主题下的概率了。
这样既可以把一个测试文档划归到一个主题下,也可以给训练文档打上主题的标记,因为我们也是可以计算训练文档它们的的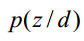 。如果从这个应用思路来说,思路一说似乎更加直接,因为其直接计算出来了
。如果从这个应用思路来说,思路一说似乎更加直接,因为其直接计算出来了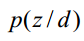 。
。
3. pLSA的优势
4. pLSA的不足
三. pLSA的Python代码实现
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np class Preprocess: def __init__(self, fname, fsw): self.fname = fname # doc info self.docs = [] self.doc_size = 0 # stop word info self.sws = [] # word info self.w2id = {} self.id2w = {} self.w_size = 0 # stop word list init with open(fsw, 'r') as f: for line in f: self.sws.append(line.strip()) def __work(self): with open(self.fname, 'r') as f: for line in f: line_strip = line.strip() self.doc_size += 1 self.docs.append(line_strip) items = line_strip.split() for it in items: if it not in self.sws: if it not in self.w2id: self.w2id[it] = self.w_size self.id2w[self.w_size] = it self.w_size += 1 self.w_d = np.zeros([self.w_size, self.doc_size], dtype=np.int) for did, doc in enumerate(self.docs): ws = doc.split() for w in ws: if w in self.w2id: self.w_d[self.w2id[w]][did] += 1 def get_w_d(self): self.__work() return self.w_d def get_word(self, wid): return self.id2w[wid] if __name__ == '__main__': fname = './data.txt' fsw = './stopwords.txt' pp = Preprocess(fname, fsw)
2. plsa.py
#!/usr/bin/env python # -*- coding: utf-8 -*- import numpy as np import time import logging def normalize(vec): s = sum(vec) for i in range(len(vec)): vec[i] = vec[i] * 1.0 / s def llhood(w_d, p_z, p_w_z, p_d_z): V, D = w_d.shape ret = 0.0 for w, d in zip(*w_d.nonzero()): p_d_w = np.sum(p_z * p_w_z[w,:] * p_d_z[d,:]) if p_d_w > 0: ret += w_d[w][d] * np.log(p_d_w) return ret class PLSA: def __init__(self): pass def train(self, w_d, Z, eps): V, D = w_d.shape # create prob array, p(d|z), p(w|z), p(z) p_d_z = np.zeros([D, Z], dtype=np.float) p_w_z = np.zeros([D, Z], dtype=np.float) p_z = np.zeros([Z], dtype=np.float) # initialize p_d_z = np.random.random([D, Z]) for d_idx in range(D): normalize(p_d_z[d_idx]) p_w_z = np.random.random([V, Z]) for w_idx in range(V): normalize(p_w_z[w_idx]) p_z = np.random.random([Z]) normalize(p_z) # iteration until converge step = 1 pp_d_z = p_d_z.copy() pp_w_z = p_w_z.copy() pp_z = p_z.copy() while True: logging.info('[ iteration ] step %d' % step) step += 1 p_d_z *= 0.0 p_w_z *= 0.0 p_z *= 0.0 # run EM algorithm for w_idx, d_idx in zip(*w_d.nonzero()): #print '[ EM ] >>>>>> E step : ' p_z_d_w = pp_z * pp_d_z[d_idx,:] * pp_w_z[w_idx,:] normalize(p_z_d_w) #print '[ EM ] >>>>>> M step : ' tt = w_d[w_idx, d_idx] * p_z_d_w p_w_z[w_idx,:] += tt p_d_z[d_idx,:] += tt p_z += tt normalize(p_w_z) normalize(p_d_z) p_z = p_z / w_d.sum() # check converge l1 = llhood(w_d, pp_z, pp_w_z, pp_d_z) l2 = llhood(w_d, p_z, p_w_z, p_d_z) diff = l2 - l1 logging.info('[ iteration ] l2-l1 %.3f - %.3f = %.3f ' % (l2, l1, diff)) if abs(diff) < eps: logging.info('[ iteration ] End EM ') return (l2, p_d_z, p_w_z, p_z) pp_d_z = p_d_z.copy() pp_w_z = p_w_z.copy() pp_z = p_z.copy()
3. main.py
#!/usr/bin/env python # -*- coding: utf-8 -*- from preprocess import Preprocess as PP from plsa import PLSA import numpy as np import logging import time def main(): # setup logging -------------------------- logging.basicConfig(filename='plsa.log', level=logging.INFO, format='%(asctime)s %(filename)s[line:%(lineno)d] %(levelname)s %(message)s', datefmt='%a, %d %b %Y %H:%M:%S') #console = logging.StreamHandler() #console.setLevel(logging.INFO) #logging.getLogger('').addHandler(console) # some basic configuration --------------- fname = './data.txt' fsw = './stopwords.txt' eps = 20.0 key_word_size = 10 # preprocess ----------------------------- pp = PP(fname, fsw) w_d = pp.get_w_d() V, D = w_d.shape logging.info('V = %d, D = %d' % (V, D)) # train model and get result ------------- pmodel = PLSA() for z in range(3, (D+1), 10): t1 = time.clock() (l, p_d_z, p_w_z, p_z) = pmodel.train(w_d, z, eps) t2 = time.clock() logging.info('z = %d, eps = %f, time = %f' % (z, l, t2-t1)) for itz in range(z): logging.info('Topic %d' % itz) data = [(p_w_z[i][itz], i) for i in range(len(p_w_z[:,itz]))] data.sort(key=lambda tup:tup[0], reverse=True) for i in range(key_word_size): logging.info('%s : %.6f ' % (pp.get_word(data[i][1]), data[i][0])) if __name__ == '__main__': main()
版权声明:
本文由笨兔勿应所有,发布于http://www.cnblogs.com/bentuwuying。如果转载,请注明出处,在未经作者同意下将本文用于商业用途,将追究其法律责任。



