归并树

定义

归并树是线段树和归并排序的合成，它利用线段树将归并排序的每一步都记录下来

例如我们对1，5，3，4，2进行归并排序，就可以生成下面的归并树

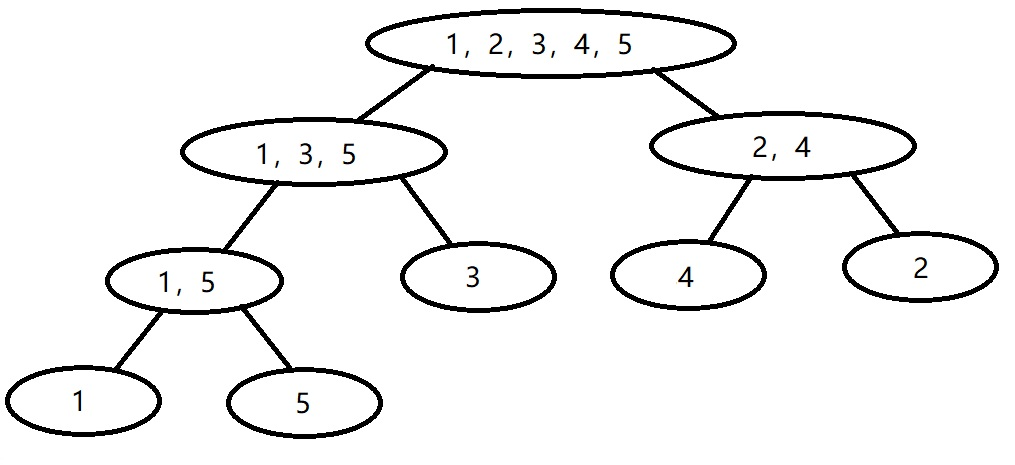
归并树的每个父节点就是两个子节点归并排序后的结果
并且归并树的叶子节点的顺序是初始序列的顺序

用处

可以快速求出在原序列的一个区间中比某个数小(大)的有多少个数

于是就可以求区间第k大问题

存储方法

我们发现归并树的每一层数字个数不会超过原数列,所以我们用一个深度*原数列长度的二维数组就可以记录下来

具体操作

• 建树

  由于每个节点是由它的两个子节点归并后构造出来的,所以我们可以递归构造子节点,回溯时构造父节点

  void build(int deep,int l,int r){//建树 
      if(l==r){Merge[deep][l]=a[l];return;}//叶子节点 
      int mid=(l+r)>>1;
      build(deep+1,l,mid),build(deep+1,mid+1,r);//先构造子节点 
      for(int i=l,j=mid+1,k=l;i<=mid||j<=r;){//归并排序构造当前节点 
          if(j>r)Merge[deep][k++]=Merge[deep+1][i++];
          else if(i>mid||Merge[deep+1][i]>Merge[deep+1][j])Merge[deep][k++]=Merge[deep+1][j++];
          else Merge[deep][k++]=Merge[deep+1][i++];
      }
  }

• 查询(原序列的一个区间中比某个数小的有多少个数)

  和线段树的区间查询差不多
  如果当前区间完全被所求区间包含,则直接二分查找出有多少个数比所给的数小
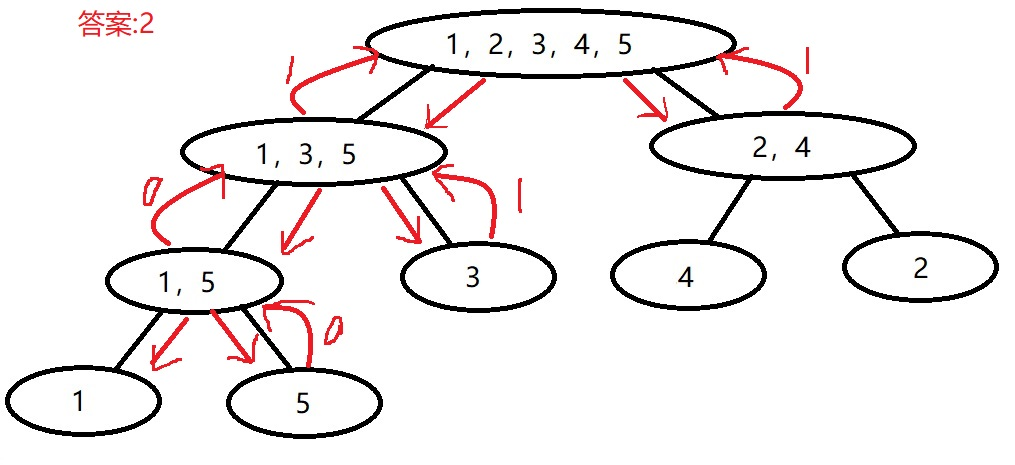
  否则,进入子节点查找,统计在两个子节点查找情况的和

  例子:在上面的归并树中查找在[2,5],有多少个数比4要小

  • 首先，[1,5]不被[2,5]包含，进入子节点
    

     

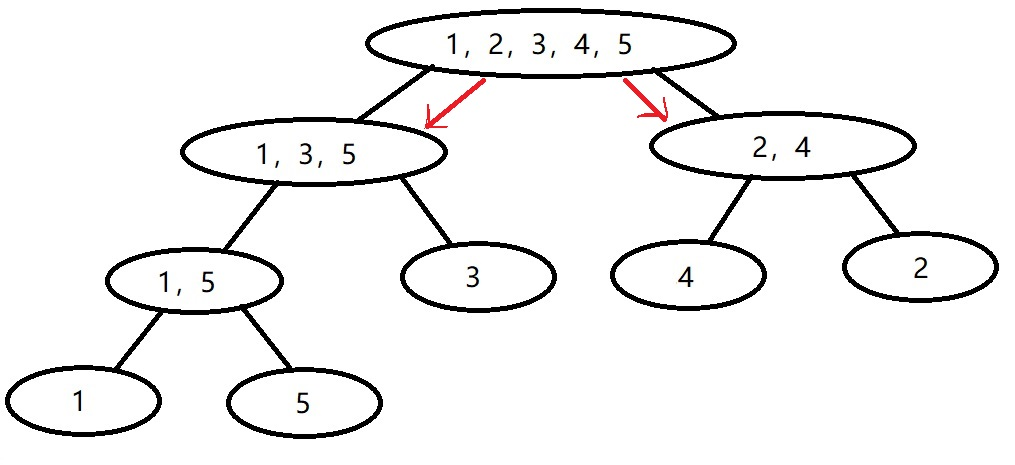
  • 然后[4,5]被[2,5]包含，二分查找返回1，[1,3]不完全被[2,5]包含，继续进入子节点<
    
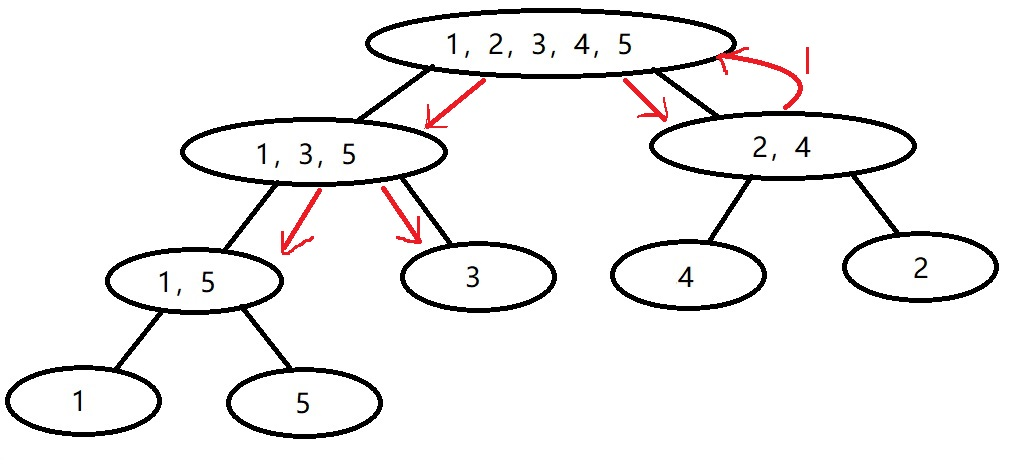
  • [3,3]被[2,5]包含,返回1，[1,2]不完全被[2,5]包含，继续进入子节点
    

     

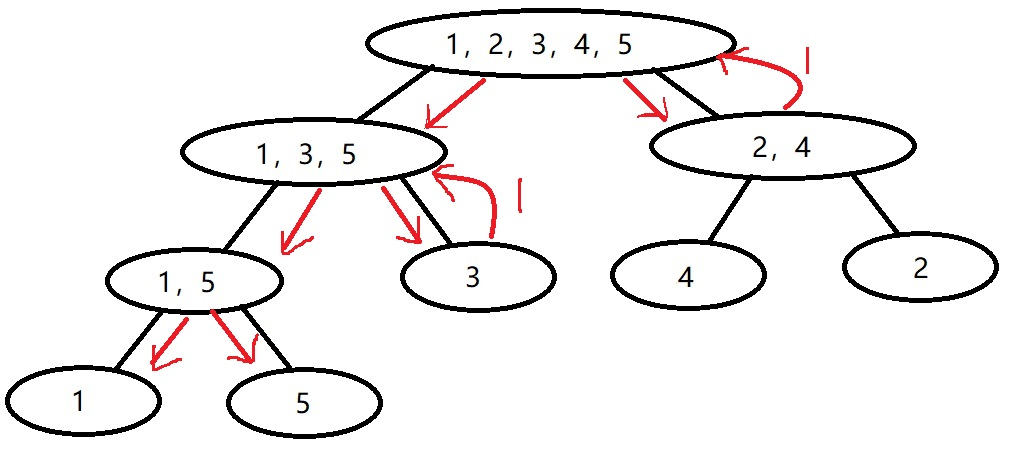
  • [1,1]不被[2,5]包含，[2,2]被[2,5]包含,返回0，最后结果是2
    

  代码实现

  int calc(int deep,int L,int R,int l,int r,int x){//计算[L,R]交[l,r]中小于x的有多少个数 
      if(L>=l&&R<=r){//[L,R]完全被[l,r]包含,直接二分查找返回 
          return lower_bound(Merge[deep]+L,Merge[deep]+R+1,x)-Merge[deep]-L;
      }
      int mid=(L+R)>>1,ans=0;//否则到子节点查找 
      if(mid>=l)ans+=calc(deep+1,L,mid,l,r,x);
      if(mid<r)ans+=calc(deep+1,mid+1,R,l,r,x);
      return ans;
  }

区间第k大值查询

二分最终排好序的序列中的值,并且在[l,r]中查找有多少个数比它小,取答案为k-1的最大的数即可

int query(int l,int r,int k){
    int L=1,R=n;
    while(L<=R){//二分查找答案 
        int mid=(L+R)>>1,cnt;
        cnt=calc(0,1,n,l,r,Merge[0][mid]);
        if(cnt<=k)L=mid+1;//<mid的肯定不是答案 
        else R=mid-1;//>=mid的肯定不是答案 
    }
    return Merge[0][L-1];//L不是答案(R不是答案,L>=R),L-2也不是答案(L=mid+1,mid-1不是答案)，答案肯定是L-1 
}

例题POJ2104 K-th Number

#include<cstdio>
#include<algorithm>
using namespace std;
#define maxn 100005
#define maxd 20
int n,m,a[maxn],Merge[maxd][maxn];
void build(int deep,int l,int r){//建树 
    if(l==r){Merge[deep][l]=a[l];return;}//叶子节点 
    int mid=(l+r)>>1;
    build(deep+1,l,mid),build(deep+1,mid+1,r);//先构造子节点 
    for(int i=l,j=mid+1,k=l;i<=mid||j<=r;){//归并排序构造当前节点 
        if(j>r)Merge[deep][k++]=Merge[deep+1][i++];
        else if(i>mid||Merge[deep+1][i]>Merge[deep+1][j])Merge[deep][k++]=Merge[deep+1][j++];
        else Merge[deep][k++]=Merge[deep+1][i++];
    }
}
int calc(int deep,int L,int R,int l,int r,int x){//计算[L,R]交[l,r]中小于x的有多少个数 
    if(L>=l&&R<=r){//[L,R]完全被[l,r]包含,直接二分查找返回 
        return lower_bound(Merge[deep]+L,Merge[deep]+R+1,x)-Merge[deep]-L;
    }
    int mid=(L+R)>>1,ans=0;//否则到子节点查找 
    if(mid>=l)ans+=calc(deep+1,L,mid,l,r,x);
    if(mid<r)ans+=calc(deep+1,mid+1,R,l,r,x);
    return ans;
}
int query(int l,int r,int k){
    int L=1,R=n;
    while(L<=R){//二分查找答案 
        int mid=(L+R)>>1,cnt;
        cnt=calc(0,1,n,l,r,Merge[0][mid]);
        if(cnt<=k)L=mid+1;//<mid的肯定不是答案 
        else R=mid-1;//>=mid的肯定不是答案 
    }
    return Merge[0][L-1];//L不是答案(R不是答案,L>=R),L-2也不是答案(L=mid+1,mid-1不是答案)，答案肯定是L-1 
}
void work(){
    for(int i=1;i<=n;i++)scanf("%d",a+i);
    build(0,1,n);
    int l,r,k;
    for(int i=0;i<m;i++){
        scanf("%d%d%d",&l,&r,&k);
        printf("%d\n",query(l,r,k-1));
    }
}
int main(){
    while(~scanf("%d%d",&n,&m))work();
    return 0;
}