acwing算法基础课III
acwing 算法基础课III.
DFS
排列数字
注意下用state表示时候的运算顺序.
取第 i 位 state >> i & 1 和 state | (1 << i);
int path[10];
int n;
void dfs(int cnt, int state) {
if (cnt == n) {
rep(i, 0, n) O(path[i]);
puts("");
return;
}
rep(i, 0, n) {
if ((state >> i & 1) == 0) { // 注意这里一定要括起来才行..
path[cnt] = i + 1;
dfs(cnt + 1, state | (1 << i));
}
}
}
int main() {
n = read();
dfs(0, 0);
return 0;
}
n-皇后问题
x+y 和 x-y+n 两个表示斜线
int n;
bool dx[30], dy[30], sy[30]; //简单的三个状态表示就行了.
char g[20][20];
void dfs(int x) {
if (x == n) {
rep(i, 0, n) {
rep(j, 0, n) printf("%c", g[i][j]);
puts("");
}
puts("");
return;
}
rep(y, 0, n) {
if (!dx[x + y] && !dy[y - x + n] && !sy[y]) {
dx[x + y] = dy[y - x + n] = sy[y] = true;
g[x][y] = 'Q';
dfs(x + 1);
dx[x + y] = dy[y - x + n] = sy[y] = false;
g[x][y] = '.';
}
}
}
int main() {
n = read();
rep(i, 0, n) rep(j, 0, n) g[i][j] = '.';
dfs(0);
return 0;
}
树的重心
DFS好处, 遍历过程中, 可以求出来子树的点的个数的.
复杂度是 \(O(n+m)\)的.
int h[N5], e[N5 * 2], ne[N5 * 2], idx, ans = N5, n;
bool st[N5]; // h是邻接表, e和ne是边.
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;// 加上一条边.
}
int dfs(int u) {
st[u] = true;
int size = 0, sum = 0;
for (int i = h[u];i != -1;i = ne[i]) {
int j = e[i];
if (st[j]) continue; // 如果 st 为 true 应该是父节点.
int s = dfs(j);
size = max(size, s);
sum += s;
}
size = max(size, n - sum - 1); // 子节点总数 + 当前 + 父节点那块 = n;
ans = min(ans, size);
return sum + 1;
}
int main() {
n = read();
memset(h, -1, sizeof h); //树初始时候 变成 -1;
rep(i, 0, n - 1) {
int a = read(), b = read();
add(a, b), add(b, a);
}
dfs(1);
O(ans);
return 0;
}
BFS
走迷宫
雪菜额外维护了一个 d[N2][N2] 来判断起点到每个点的距离.
char g[N2][N2];
int dx[4] = { 1,-1,0,0 }, dy[4] = { 0,0,-1,1 };
int main() {
queue<PII> q;
int n = read(), m = read();
rep(i, 0, n)rep(j, 0, m) g[i][j] = read();
q.push({ 0,0 });
g[0][0] = 1;
int res = 0;
while (q.size()) {
res++;
int cnt = q.size();
while (cnt--) {
auto t = q.front();
rep(i, 0, 4) {
int x = t.first + dx[i], y = t.second + dy[i];
if (x == n - 1 && y == m - 1) {
O(res); return 0;
}
if (x >= 0 && x < n && y >= 0 && y < m && !g[x][y])
q.push({ x,y }), g[x][y] = 1; // ... 等于 写成 == 导致无限循环...
}
q.pop();
}
}
return 0;
}
八树码
注意是 unordered_set 不是 set ... 要不然会 TLE;
int dx[] = { 1,-1,0,0 }, dy[] = { 0,0,1,-1 };
unordered_set<string> ss;
string res = "12345678x";
int main() {
string s;
char op[3];
rep(i, 0, 9) { cin >> op; s += op[0]; }
queue<string> que;
if (s == res) { O(0);return 0; }
que.push(s);
int ans = 1;
while (!que.empty())
{
int cnt = que.size();
while (cnt--) {
s = que.front(); que.pop();
int p = s.find('x');
rep(i, 0, 4) {
int x = p / 3 + dx[i], y = p % 3 + dy[i];
if (x >= 0 && x < 3 && y >= 0 && y < 3) {
swap(s[x * 3 + y], s[p]);
if (!ss.count(s)) {
ss.insert(s), que.push(s);
if (s == res) { O(ans);return 0; }
}
swap(s[x * 3 + y], s[p]);
}
}
}
ans++;
}
O(-1);
return 0;
}
图中点的层次
int n, m, e[N5], h[N5], ne[N5], idx, st[N5];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;// 加上一条边.
}
int main() {
n = read(), m = read();
memset(h, -1, sizeof h); //树初始时候 变成 -1;
rep(i, 0, m) {
int a = read(), b = read();
add(a, b);
}
queue<int> qu;
qu.push(1);
int res = 0;
while (!qu.empty()) {
int cnt = qu.size();
while (cnt--) {
int t = qu.front();
if (t == n) { O(res);return 0; }
for (int i = h[t];i != -1;i = ne[i]) {
int j = e[i]; // 记住这样才能把边取出来
if (!st[j]) {
st[j] = true;
qu.push(j);
}
}
qu.pop();
}
res++;
}
O(-1);
return 0;
}
拓扑排序
有向图拓扑排序
使用自定义的队列, 可以存下来 拓扑排序的顺序, 妙啊;
const int N = N5;
int n, m, h[N], e[N], ne[N], q[N], d[N], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool bfs() {
int hh = 0, tt = -1;
rep(i, 1, n + 1) {
if (!d[i]) q[++tt] = i;
}
while (hh <= tt) {
int t = q[hh++];
// cout << t << endl;
for (int i = h[t]; i != -1;i = ne[i]) {
int j = e[i];
// cout << " " << j << endl;
if (--d[j] == 0) q[++tt] = j;
}
}
return hh == n; // 注意这里 hh是n 而 tt是 n-1;
}
int main() {
n = read(), m = read();
memset(h, -1, sizeof h);
rep(i, 0, m) {
int a = read(), b = read();
add(a, b);
d[b]++;
}
if (bfs()) { rep(i, 0, n)O(q[i]); }
else { O(-1); }
return 0;
}
最短路
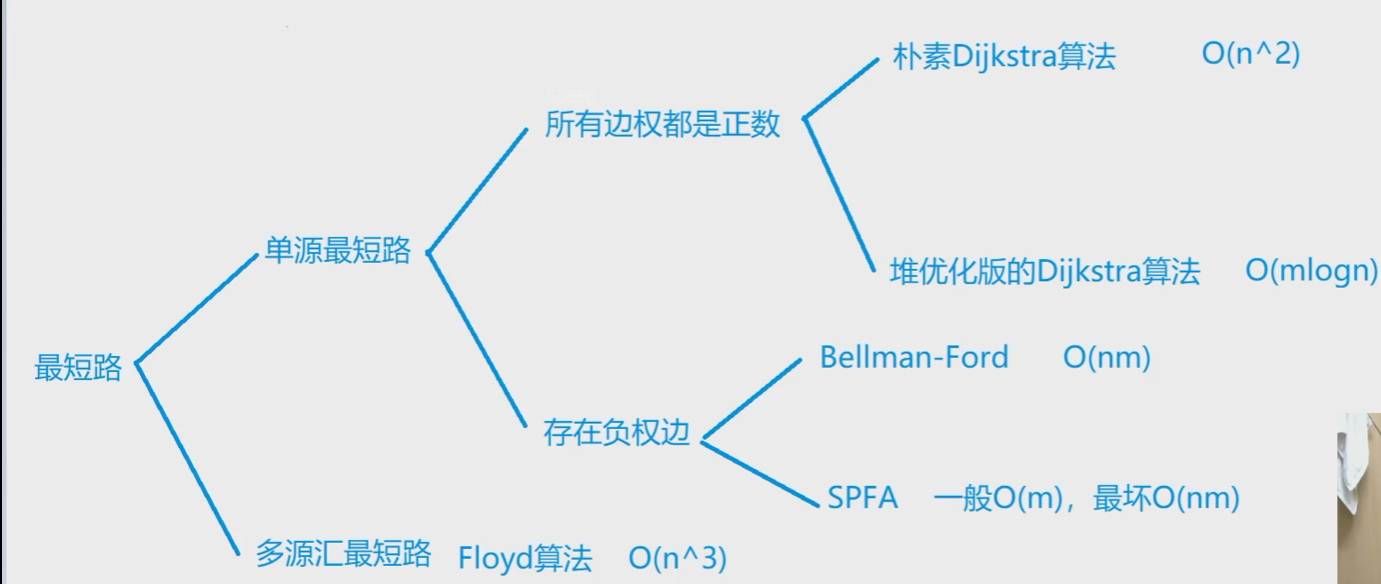
单源最短路.
- 所有边权都是正的. 朴素 Dijkstra \(O(n^2)\) 和 堆优化的Dijkstra算法 \(O(mlogn)\).
- 存在负权边. Bellman-Ford \(O(nm)\) SPFA 一般\(O(m)\) 最坏\(O(nm)\)
- 如果限制经过不超过 \(k\) 条边的话, 只能用 bellman-ford 算法
多源汇最短路: 多个起点和多个起点的最短路. 都是不确定的.
- Floyd 算法 \(O(n^3)\)
问题: 建图..
dijkstra 最短路
遍历过的边 S 和其他的边 T之间, 每次从T最小 dis 的 放到 S中, 然后更新T中其他边的距离, a,b,w 有 dis[a] + w < dis[b] 就更新一下.
边权一定得是正数.
dist[1] = 0, dist[v] = +inf //其他初始化成正无穷for v: 0 ~ n\(O(n)\)- 不在 S 中的距离最近的点\(\to\)
t\(O(n)\) - t \(\to\) S
- 用
t更新其他点的距离:t的所有的边,dist[x] > dist[t] + w更新一下. \(O(n)\)
- 不在 S 中的距离最近的点\(\to\)
const int N = 500 + 10;
int dist[N];
int g[N][N];
bool st[N];
int n, m, t;
int dijkstra() {
dist[1] = 0;
rep(j, 0, n - 1) { // 只需要 n - 1次, 因为最后只剩一个点了.
t = -1;
rep(i, 1, n + 1)
if (!st[i] && (t == -1 || dist[i] < dist[t])) t = i;
if(t == n) break;
st[t] = true;
rep(i, 1, n + 1)
dist[i] = min(dist[i], dist[t] + g[t][i]);
// On(dist[n]);
}
return dist[n] == 0x3f3f3f3f ? -1 : dist[n];
}
int main() {
n = read(), m = read();
memset(g, 0x3f, sizeof g);
memset(dist, 0x3f, sizeof dist);
while (m--) {
int a = read(), b = read(), w = read();
g[a][b] = min(g[a][b], w);
}
O(dijkstra());
return 0;
}
dijkstra 最短路2:
用堆来维护接下来需要遍历的边.
const int N = 1.5e5 + 10;
int n, m, ne[N], w[N], h[N], e[N], dist[N], idx, x;
bool st[N];
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int diskstra() {
pqs(PII) heap;
dist[1] = 0;
heap.push({ 0,1 });
while (!heap.empty()) {
auto top = heap.top();
heap.pop();
int distance = top.first, x = top.second; // haha 这里写反了...
if (st[x]) continue;
st[x] = true;
for (int i = h[x];i != -1;i = ne[i]) {
int j = e[i];
if (dist[x] + w[i] < dist[j]) {
dist[j] = dist[x] + w[i],
heap.push({ dist[j],j });
}
}
}
return dist[n] == 0x3f3f3f3f ? -1 : dist[n];
}
int main() {
memset(h, -1, sizeof h);
memset(dist, 0x3f, sizeof dist);
n = read(), m = read();
while (m--) {
int a = read(), b = read(), c = read();
add(a, b, c);
}
O(diskstra());
return 0;
}
Bellman-ford 最短路 ↪️
-
for 1 : n
- for 所有边
a,b,w. 开结构体. 随便存 dist[b] = min(dist[b], dist[a] + w)松弛操作.
循环完成以后有
dist[b] <= dist[a] + w - for 所有边
多少条边 遍历多少次. 直接用结构体存就可以.
然后可以判断负环, 如果存在, n次遍历以后还在更新, 那么就说明有一条大于n长度的最短路径, 也就是说有负环.
O(nm)的算法.
最多k条边的最短路径, 只能用bellman-ford
每次备份一下 当前的dis数组, 才能保证在 k 的限制之内. memcpy
struct {
int a, b, w;
}edges[N4];
int n, m, k, dist[N4], backup[N4];
int main() {
n = read(), m = read(), k = read();
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
rep(i, 0, m) {
int a = read(), b = read(), w = read();
edges[i] = { a,b,w };
}
rep(i, 0, k) {
memcpy(backup, dist, sizeof dist);
rep(i, 0, m) {
int a = edges[i].a, b = edges[i].b, w = edges[i].w;
dist[b] = min(dist[b], backup[a] + w);
// 这里错了.... 要怎么改呢? 备份一下dist ?
}
}
if (dist[n] >= 0x3f3f3f3f / 2) puts("impossible");
else O(dist[n]);
}
spfa
由 dis[b] = min(dis[b], dis[a]+w) 如果 dis[a] 不变的话, dis[b] 也不会变.
BFS进行, 如果变小, 就加入队列, 反复迭代.
- node1 \(\to\) queue
- while(!queue.empty())
- t <- q.front.
- 更新
t的所有出边. b <- t . queue <- b; //这里 t 代表着 dist[a] 变小了.
int n, m, h[N5], w[N5], ne[N5], e[N5], idx, dist[N5];
bool st[N5];
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
void spfa() {
queue<int> que;
que.push(1), st[1] = true;
// O(n);
while (!que.empty()) {
int a = que.front(); que.pop(); st[a] = false;
for (int i = h[a]; i != -1; i = ne[i]) {
int b = e[i], c = w[i];
if (dist[b] > dist[a] + c) {
dist[b] = dist[a] + c;
if (!st[b]) {
// 这里一定要加上判断 st[b] .. yes 不加的话. st就没用了啊...
que.push(b);
st[b] = true;
}
}
}
da(dist, n + 1);
}
}
int main() {
n = read(), m = read();
memset(h, -1, sizeof h);
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
rep(i, 0, m) {
int a = read(), b = read(), c = read();
add(a, b, c);
}
spfa();
if (dist[n] >= 0x3f3f3f3f / 2) puts("impossible");
else O(dist[n]);
}
spfa求负环
路径上一定存在一个环.
初始时候每个边都放到queue中, 然后求得时候用cnt[N]如果大于了 n 就说明有负环了.
- 进行更新
dist[b] = dist[a] + w的时候就cnt[b] = cnt[a] + 1说明多了一条边 - 如果某一次
cnt[b] >= n了 那就说明已经有负环了, 抽屉原理.
int n, m, h[N5], w[N5], ne[N5], e[N5], idx, dist[N5], cnt[N5];
bool st[N5];
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
bool spfa() {
queue<int> que;
rep(i, 1, n + 1) que.push(i), st[i] = true; //I. 这里好像要每个点都push进去.
// O(n);
while (!que.empty()) {
int a = que.front(); que.pop(); st[a] = false;
for (int i = h[a]; i != -1; i = ne[i]) {
int b = e[i], c = w[i];
if (dist[b] > dist[a] + c) {
dist[b] = dist[a] + c;
cnt[b] = cnt[a] + 1; //II. 是这样更新的.....
if (cnt[b] >= n) return true;
if (!st[b]) {
que.push(b);
st[b] = true;
}
}
}
da(dist, n + 1);
}
return false;
}
int main() {
n = read(), m = read();
memset(h, -1, sizeof h);
rep(i, 0, m) {
int a = read(), b = read(), c = read();
add(a, b, c);
}
puts(spfa() ? "Yes" : "No");
}
Floyd最短路
多源汇最短路问题. 输出很多..
d[k, i, j] 表示只经过前k 个点, 从 i 到 j 的最短距离.
d[k,i,j] (min=) d[k-1, i, k] + d[k-1, k, j] 加上第 k 个点, 会不会变短.
动态规划.
不能有负权回路, 负无穷的最短路径.
const int N = 210, M = N4 * 2, INF = 0x3f3f3f3f;
int n, m, k, x, d[N][N]; // I. 这里的 g 和 d 可以共用一个东西.
int main() {
n = read(), m = read(), k = read();
rep(i, 1, n + 1)
rep(j, 1, n + 1)
if (i == j) d[i][i] = 0; // II. 这里的初始化可以memset(inf)?? 没错.
else d[i][j] = INF;
rep(i, 0, m) {
int a = read(), b = read(), c = read();
d[a][b] = min(d[a][b], c);
}
rep(k, 1, n + 1) { // III 遍历所有 k 条边
rep(i, 1, n + 1)
rep(j, 1, n + 1) // IV 遍历所有 i -> j 的路径
d[i][j] = min(d[i][j], d[i][k] + d[k][j]); // V 可以变成 i -> j -> k 吗?
}
rep(i, 0, k) {
int a = read(), b = read();
if (d[a][b] > INF / 2) puts("impossible");
else On(d[a][b]);
}
}
生成树.

prim 最小生成树
一般都是无向图 (可以处理负权的树.)
任意两个城市之间铺公路的最小长度.
- 所有 dist[i] 初始化成正无穷
- rep(i,0,n)
- t \(\leftarrow\) 集合外距离最近的点. (第一步随便挑)
- 用t来更新其他点到集合的距离 // 只有和disktra不同. 有没有一条边能连向集合内部.
- st[t] = true 加入到集合中.
- 只有集合这里和dijkstra不同.
const int N = 510, M = N4 * 2, INF = 0x3f3f3f3f;
int n, m, k, x, d[N][N], dist[N];
bool st[N];
int main() {
n = read(), m = read();
memset(dist, 0x3f, sizeof dist);
rep(i, 1, n + 1)
rep(j, 1, n + 1)
if (i == j) d[i][i] = 0;
else d[i][j] = INF;
rep(i, 0, m) {
int a = read(), b = read(), c = read();
d[a][b] = d[b][a] = min(d[a][b], c);
}
int ans = 0;
dist[1] = 0; // I 这里切记不敢让 st[1] = true 了.
rep(j, 0, n) { // O(n)
int t = -1;
rep(i, 1, n + 1) if (!st[i] && (t == -1 || dist[i] < dist[t])) t = i; // O(n)
st[t] = true;
// II. 找到 dist 最小的点. 并 更新状态.
if (dist[t] >= INF / 2) { ans = INF;break; }
// III. 如果不连通, false ;
ans += dist[t]; // IV: 当前距离加入到生成树中 需要在 V. 前面才能处理自环.
rep(i, 1, n + 1) dist[i] = min(dist[i], d[t][i]);
// V: 更新集合外其他点的距离. O(n)
}
if (ans >= INF / 2) puts("impossible");
else O(ans);
} // O(n^2)
//todo 堆优化. 基本可以被 kruskal 取代掉, 所以不用了.
kruskal
- 将所有边按照权重从大到小排序.
- O(m logm) 常数非常小
- 枚举每条边, a,b,w 如果a, b 不连通, 将w加到集合中.
- 并查集. O(m)
const int M = 2 * N5;
int p[N5];
vector<pair<int, PII>> e;
struct Edge{
int a, b, w;
bool operator< (const Edge &W)const // I. 如何重载 比较符.
{
return w < W.w;
}
}
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main() {
int n = read(), m = read();
rep(i, 0, m) {
int a = read(), b = read(), c = read();
e.push_back({ c,{a,b} });
}
sort(e.begin(), e.end()); // O(mlogm) I. 所有边需要进行排序.
rep(i, 1, n + 1) p[i] = i;
int ans = 0, cnt = 0;
for (auto i : e) { // O(m) 并查集好像是 O(logm) 的? 不过有剪枝.
int w = i.first, a = i.second.first, b = i.second.second;
if (find(a) != find(b)) {
ans += w; // II. 从小到大遍历, 把最小的边加进来.
cnt++;
p[find(a)] = find(b);
}
}
if (cnt != n - 1) puts("impossible");
else O(ans);
return 0;
}
二分图
一个图是二分图, 当且仅当图中不含奇数环.
染色法.
判断是否是二分图.
给一个图进行 dfs 染色, 如果 染色出现矛盾以后, 就不是一个二分图了.
int n, m, c[N5], e[N5 * 2], h[N5], ne[N5 * 2], idx;
// I. 注意 边的个数要是原来的 2 倍才行
// II. st 可以直接用 c 代替就行...
bool ok = true;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int a, int w) {
if (!ok) return;
c[a] = w;
for (int i = h[a]; i != -1;i = ne[i]) {
int j = e[i];
if (c[j]) { if (c[j] != 3 - w) ok = false; }
// I. 染色的时候用 3 - w 判断二分图的两边.
else dfs(j, 3 - w);
}
}
int main() {
n = read(), m = read();
memset(h, -1, sizeof h);
rep(i, 0, m) {
int a = read(), b = read();
add(a, b), add(b, a); // 无向图.
}
rep(i, 1, n + 1) {
if (!c[i]) dfs(i, 1); // 每个点都需要染色.
}
puts(ok ? "Yes" : "No");
return 0;
}
匈牙利算法 二分图匹配
返回图中匹配成功的数量最大值.
如果想要去匹配的人已经有人了, 那就尝试换一个.
O(n * m) 实际时间 远小于 O(n * m)
这个回溯怎么写的还是没懂..
// 好像是个递归吗?
const int N = 500, M = 1e5;
int n1, n2, m, e[M], h[N], ne[M], idx;
bool st[N];
int match[N]; // I. 需要一个 match 数组存放当前的匹配.
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool find(int x) {
for (int i = h[x]; i != -1; i = ne[i]) { // O(m);
int j = e[i];
if (!st[j]) { // 如果还没有遍历过. 遍历过了, 也能跳过, 防止递归那里出问题.
st[j] = true; // 这个用 st 是很好的东西, 是否遍历过
if (!match[j] || find(match[j])) { // 如果还没有, 或者 能找到新的, 这里是个递归.
match[j] = x;
return true;
}
}
}
return false;
}
int main() {
n1 = read(), n2 = read(), m = read();
memset(h, -1, sizeof h);
rep(i, 0, m) {
int a = read(), b = read();
add(a, b);
}
int ans = 0;
rep(i, 1, n1 + 1) { // O(n)
memset(st, 0, sizeof st); // 开始前每一次需要全部初始化成 0;
if (find(i)) ans++;
}
O(ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号