51Nod 1242 斐波那契数列的第N项(难度:基础题)
斐波那契数列的定义如下:
F(0) = 0
F(1) = 1
F(n) = F(n - 1) + F(n - 2) (n >= 2)(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …)
给出n,求F(n),由于结果很大,输出F(n) % 1000000009的结果即可。
Input
输入1个数n(1 <= n <= 10^18)。
Output
输出F(n) % 1000000009的结果。
Input示例
11
Output示例
89
矩阵快速幂, 关于快速幂,过段时间整理一篇
简单缕一下吧:相当于公式
代码:

1 #include<iostream> 2 #include<cstring> 3 #include<cmath> 4 #define mod 1000000009 5 using namespace std; 6 struct mat{ 7 long long m[100][100]; 8 }; 9 mat map,sum; 10 long long N; 11 mat muliply(mat a,mat b) 12 { 13 mat c; 14 memset(c.m,0,sizeof(c.m)); 15 for(long long i=0;i<2;i++) 16 for (long long j=0;j<2;j++) 17 for (long long z=0;z<2;z++) 18 { 19 c.m[i][j]+=a.m[i][z]*b.m[z][j]; 20 c.m[i][j]%=mod; 21 } 22 return c; 23 } 24 mat poww(mat a,long long n) 25 { 26 memset(sum.m,0,sizeof(sum.m)); 27 for (long long i=0;i<2;i++) 28 sum.m[i][i]=1; 29 while(n) 30 { 31 if (n&1) 32 sum=muliply(sum,a); 33 a=muliply(a,a); 34 n>>=1; 35 } 36 return sum; 37 } 38 int main() 39 { 40 while (scanf("%lld",&N)!=EOF) 41 { 42 map.m[0][0]=1; 43 map.m[0][1]=1; 44 map.m[1][0]=1; 45 map.m[1][1]=0; 46 if (N==1) 47 { 48 printf("%lld\n",1); 49 continue; 50 } 51 sum=poww(map,N); 52 printf("%lld\n",sum.m[1][0]%mod); 53 54 } 55 return 0; 56 }

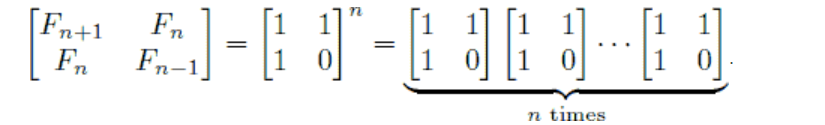


 浙公网安备 33010602011771号
浙公网安备 33010602011771号