2022-1-17图day5
题1:
给你一个points 数组,表示 2D 平面上的一些点,其中 points[i] = [xi, yi] 。
连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 :|xi - xj| + |yi - yj| ,其中 |val| 表示 val 的绝对值。
请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时,才认为所有点都已连接。
示例 1:
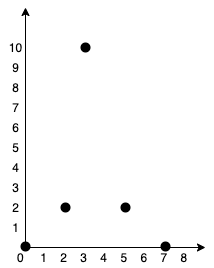
输入:points = [[0,0],[2,2],[3,10],[5,2],[7,0]] 输出:20 解释:

我们可以按照上图所示连接所有点得到最小总费用,总费用为 20 。 注意到任意两个点之间只有唯一一条路径互相到达。
示例 2:
输入:points = [[3,12],[-2,5],[-4,1]] 输出:18
示例 3:
输入:points = [[0,0],[1,1],[1,0],[-1,1]] 输出:4
示例 4:
输入:points = [[-1000000,-1000000],[1000000,1000000]] 输出:4000000
示例 5:
输入:points = [[0,0]] 输出:0
提示:
1 <= points.length <= 1000-106 <= xi, yi <= 106- 所有点
(xi, yi)两两不同。
1 class Solution { 2 3 class Unionfind{ 4 int[] parent; 5 int[] size; 6 Unionfind(int n){ 7 parent = new int[n]; 8 size = new int[n]; 9 Arrays.fill(size,1); 10 for (int i=0;i<n;i++) parent[i]=i; 11 } 12 13 public void union(int x,int y){ 14 int rootx=find(x),rooty=find(y); 15 if (rootx==rooty) return; 16 else{ 17 if (size[rootx]>size[rooty]) { 18 parent[rootx]=rooty; 19 size[rooty]+=size[rootx]; 20 }else { 21 parent[rooty]=rootx; 22 size[rootx]+=size[rooty]; 23 } 24 } 25 } 26 27 public int find(int x){ 28 while (parent[x]!=x){ 29 parent[x]=parent[parent[x]]; 30 x=parent[x]; 31 } 32 return x; 33 } 34 35 public boolean isConnect(int x,int y){ 36 return find(x)==find(y); 37 } 38 } 39 public int minCostConnectPoints(int[][] points) { 40 PriorityQueue<int[]> queue=new PriorityQueue<>((a,b)->(a[0]-b[0])); 41 for (int i=0;i<points.length-1;i++) { 42 for (int j=i+1;j<points.length;j++){ 43 int val=Math.abs(points[i][0]-points[j][0])+Math.abs(points[i][1]-points[j][1]); 44 int[] a=new int[3]; 45 a[0]=val; 46 a[1]=i; 47 a[2]=j; 48 queue.offer(a); 49 } 50 } 51 int n=points.length; 52 Unionfind unionfind=new Unionfind(n); 53 int ans=0,num=0; 54 while (!queue.isEmpty()&&num!=n){ 55 int[] temp=queue.poll(); 56 if (unionfind.isConnect(temp[1],temp[2])) continue; 57 else { 58 unionfind.union(temp[1],temp[2]); 59 ans+=temp[0]; 60 num++; 61 } 62 } 63 return ans; 64 } 65 }
思路 :kruskal最小生成树思想。把所有边从小到大排序,遍历所有边,如果边的顶点没有连通,加入这条边,同时将顶点连通。维护顶点连通用并查集的结构。



