2022-1-15图day3

题1：

785. 判断二分图labuladong 题解思路

存在一个 无向图 ，图中有 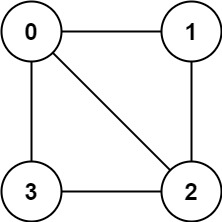n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：

• 不存在自环（graph[u] 不包含 u）。
• 不存在平行边（graph[u] 不包含重复值）。
• 如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
• 这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。

二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

如果图是二分图，返回 true ；否则，返回 false 。

 

示例 1：

输入：graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
输出：false
解释：不能将节点分割成两个独立的子集，以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。

示例 2：

输入：graph = [[1,3],[0,2],[1,3],[0,2]]
输出：true
解释：可以将节点分成两组: {0, 2} 和 {1, 3} 。

 

提示：

• graph.length == n
• 1 <= n <= 100
• 0 <= graph[u].length < n
• 0 <= graph[u][i] <= n - 1
• graph[u] 不会包含 u
• graph[u] 的所有值 互不相同
• 如果 graph[u] 包含 v，那么 graph[v] 也会包含 u

class Solution {
    boolean[] visit;
    int[] color;
    boolean ok=true;
    public boolean isBipartite(int[][] graph) {
        int n=graph.length;
        visit=new boolean[n];
        color=new int[n];
        for (int i=0;i<n;i++){
            if (!visit[i]) check(graph,i);
        }
        return ok;
    }

    public void check(int[][] graph,int x){
        if (!ok) return;
        visit[x]=true;
        for (int node:graph[x]){
            if  (!visit[node]){
                //没染色，需要染色
                if (color[x]==0) color[node]=1;
                else color[node]=0;
                check(graph,node);
            }else {
                //判断是否不同色
                if (color[x]+color[node]!=1) ok=false;
            }
        }
    }
}

思路：二分图染色法，相邻节点要不同颜色0和1。

题2：

886. 可能的二分法labuladong 题解思路

给定一组 N 人（编号为 1, 2, ..., N）， 我们想把每个人分进任意大小的两组。

每个人都可能不喜欢其他人，那么他们不应该属于同一组。

形式上，如果 dislikes[i] = [a, b]，表示不允许将编号为 a 和 b 的人归入同一组。

当可以用这种方法将所有人分进两组时，返回 true；否则返回 false。

 

示例 1：

输入：N = 4, dislikes = [[1,2],[1,3],[2,4]]
输出：true
解释：group1 [1,4], group2 [2,3]

示例 2：

输入：N = 3, dislikes = [[1,2],[1,3],[2,3]]
输出：false

示例 3：

输入：N = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]]
输出：false

 

提示：

• 1 <= N <= 2000
• 0 <= dislikes.length <= 10000
• dislikes[i].length == 2
• 1 <= dislikes[i][j] <= N
• dislikes[i][0] < dislikes[i][1]
• 对于 dislikes[i] == dislikes[j] 不存在 i != j

class Solution {
    boolean[] visit;
    boolean flag=true;
    boolean[] color;
    public boolean possibleBipartition(int n, int[][] dislikes) {
        List<List<Integer>> graph=build(n,dislikes);
        visit=new boolean[n];
        color=new boolean[n];
        for (int i=0;i<n;i++){
            if (!visit[i]) transer(graph,i);
        }
        return flag;
    }


    public List<List<Integer>> build(int n,int[][] dislikes){
        List<List<Integer>> list=new ArrayList<>();
        for (int i=0;i<n;i++){
            list.add(new ArrayList<>());
        }
        for (int[] x:dislikes) {
            list.get(x[0]-1).add(x[1]-1);
            //讨厌是互相的，所以加两条边
            list.get(x[1]-1).add(x[0]-1);
        }
        return list;
    }

    public void transer(List<List<Integer>> list,int x){
        if (!flag) return;
        visit[x]=true;
        for (int node:list.get(x)){
            if (!visit[node]) {
                color[node]=!color[x];
                transer(list,node);
            }else {
                if (color[x]==color[node]) flag=false;
            }
        }
    }
}

思路：也是二分图染色问题，区别在于互相讨厌的数组需要先建立邻接表。注意，邻接表双向图，所以两个节点都得加上边。