2022-1-11二叉搜索树day2

题1：

700. 二叉搜索树中的搜索labuladong 题解思路

给定二叉搜索树（BST）的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 NULL。

例如，

给定二叉搜索树:

        4
       / \
      2   7
     / \
    1   3

和值: 2

你应该返回如下子树:

      2     
     / \   
    1   3

在上述示例中，如果要找的值是 5，但因为没有节点值为 5，我们应该返回 NULL。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if (root==null){
            return root;
        }
        if (root.val>val){
            return searchBST(root.left,val);
        }else if (root.val<val){
            return searchBST(root.right,val);
        }else{
            return root;
        }
    }
}

思路：按照左小右大的思路递归搜索。

题2：

98. 验证二叉搜索树labuladong 题解思路

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

 

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

 

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        return BST(root,null,null);
    }

    public boolean BST(TreeNode root,TreeNode max,TreeNode min) {
        if (root==null) return true;
        if (max!=null&&root.val>=max.val) return false;
        if (min!=null&&root.val<=min.val) return false;
        return BST(root.left,root,min)&&BST(root.right,max,root);
    }
}

思路：注意除了普通的左子树右子树递归判断外，左子树最大不超过根节点， 右子树最小不小于根节点。

题3：

701. 二叉搜索树中的插入操作labuladong 题解思路

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

 

示例 1：

输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

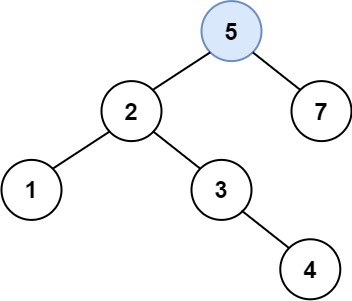
示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

 

 

提示：

• 给定的树上的节点数介于 0 和 10^4 之间
• 每个节点都有一个唯一整数值，取值范围从 0 到 10^8
• -10^8 <= val <= 10^8
• 新值和原始二叉搜索树中的任意节点值都不同

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root==null) return new TreeNode(val);
        else if (root.val>val) {
            root.left=insertIntoBST(root.left,val);
        }else root.right=insertIntoBST(root.right,val);
        return root;
    }
}

题4：

450. 删除二叉搜索树中的节点labuladong 题解思路

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

 

示例 1:

输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

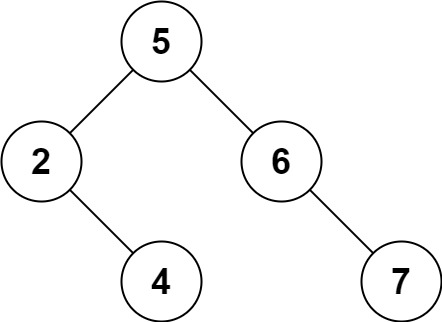
示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

 

提示:

• 节点数的范围 [0, 104].
• -105 <= Node.val <= 105
• 节点值唯一
• root 是合法的二叉搜索树
• -105 <= key <= 105

 

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        //没找到 返回null
        if (root==null) return null;
        if (root.val==key) {
            //找到值，返回不空的子树替代，两个都空的情况也处理了
            if (root.left==null||root.right==null) return root.left==null?root.right:root.left;
            //两个子树都不空，将左子树最大的节点替代 或者右子树最小的节点替代。
            TreeNode maxNode=get(root.left);
            root.val=maxNode.val;
            //替代值后，将左子树这个节点删除
            root.left=deleteNode(root.left,maxNode.val);
        }else if (root.val>key) {
            root.left=deleteNode(root.left,key);
        }else root.right=deleteNode(root.right,key);
        return root;
    }

    public TreeNode get(TreeNode root){
        if (root.right==null) return root;
        else return get(root.right);
    }
}