2022-1-10二叉搜索树day1

题1:

230. 二叉搜索树中第K小的元素labuladong 题解思路

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

 

示例 1：

输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

 

 

提示：

• 树中的节点数为 n 。
• 1 <= k <= n <= 104
• 0 <= Node.val <= 104

 

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int kthSmallest(TreeNode root, int k) {
        int left=size(root.left);
        if (left==k-1) return root.val;
        if (left>k-1) return kthSmallest(root.left,k);
        else return kthSmallest(root.right,k-left-1);
    }

    public int size(TreeNode root) {
        if (root==null) return 0;
        return size(root.left)+size(root.right)+1;
    }

}

思路：根据二叉 搜索树的性质，根节点左边都较小，根节点右边都较大，所以左子树的数量为left，则根节点就是第left+1个数。

因此如果左结点left==k-1,根节点就是第k个数，left>k-1时，说明第k个在左子树，递归调用查找左子树中第k个；

如果left<k-1,说明在右子树中，递归调用查找右子树中k-left-1个。

题2：

538. 把二叉搜索树转换为累加树labuladong 题解思路

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

• 节点的左子树仅包含键 小于 节点键的节点。
• 节点的右子树仅包含键 大于 节点键的节点。
• 左右子树也必须是二叉搜索树。

注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

 

示例 1：

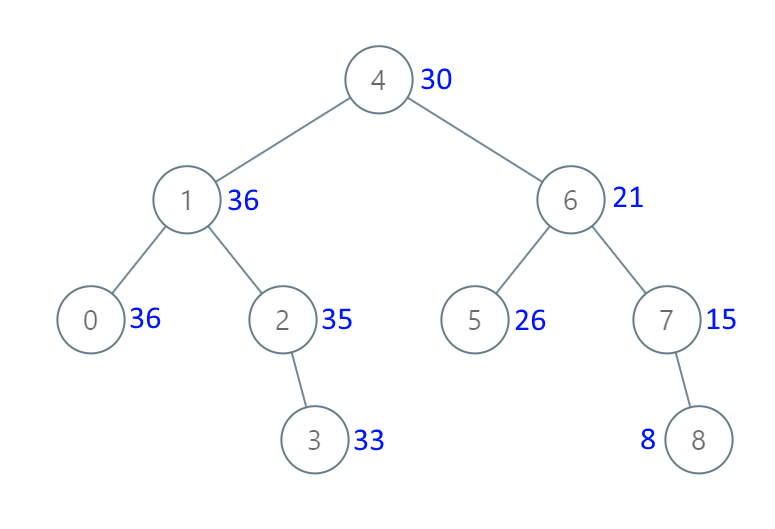
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

 

提示：

• 树中的节点数介于 0 和 104 之间。
• 每个节点的值介于 -104 和 104 之间。
• 树中的所有值 互不相同 。
• 给定的树为二叉搜索树。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int sum;
    public TreeNode convertBST(TreeNode root) {
        build(root);
        return root;
    }


    public void build(TreeNode root) {
        if (root==null) return;
        build(root.right);
        sum+=root.val;
        root.val=sum;
        build(root.left);
    }
}

思路： 中序遍历是从小到大排序，反过来就是从大到小，sum累加，然后改变当前节点的值，从大到小依次递归生成即可。