2021-12-24数组链表day1

题1：

303. 区域和检索 - 数组不可变labuladong 题解思路

给定一个整数数组  nums，求出数组从索引 i 到 j（i ≤ j）范围内元素的总和，包含 i、j 两点。

实现 NumArray 类：

• NumArray(int[] nums) 使用数组 nums 初始化对象
• int sumRange(int i, int j) 返回数组 nums 从索引 i 到 j（i ≤ j）范围内元素的总和，包含 i、j 两点（也就是 sum(nums[i], nums[i + 1], ... , nums[j])）

 

示例：

输入：
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出：
[null, 1, -1, -3]

解释：
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1)) 
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))

 

提示：

• 0 <= nums.length <= 104
• -105 <= nums[i] <= 105
• 0 <= i <= j < nums.length
• 最多调用 104 次 sumRange 方法

class NumArray {
    int[] sum;
    public NumArray(int[] nums) {
        int s=0;
        sum=new int[nums.length];
        for (int i=0;i<nums.length;i++){
            s+=nums[i];
            sum[i]=s;
        }
    }
    
    public int sumRange(int left, int right) {
        if (left==0) return sum[right];
        else return sum[right]-sum[left-1];
    }
}

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * int param_1 = obj.sumRange(left,right);
 */

前缀和思想。

题2：

304. 二维区域和检索 - 矩阵不可变labuladong 题解思路

给定一个二维矩阵 matrix，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

 

示例 1：

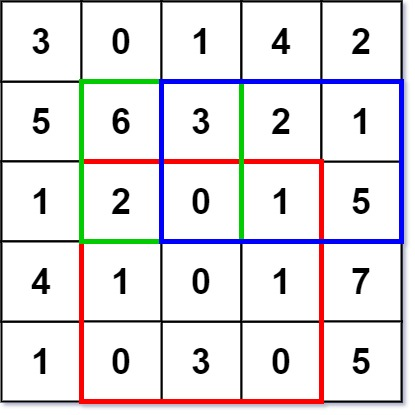
输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

 

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• -105 <= matrix[i][j] <= 105
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• 最多调用 104 次 sumRegion 方法

同理，利用前缀和的思想求出 每个角点的和，再利用减法求每一块的sum

class NumMatrix {
    int[][] sum;
    public NumMatrix(int[][] matrix) {
        int m=matrix.length,n=matrix[0].length;
        sum=new int[m+1][n+1];
        // 避免边界讨论
        for(int i=1;i<m+1;i++){
            int s=0;
            //计算该行的和
            for(int j=1;j<n+1;j++){
                s+=matrix[i-1][j-1];
                //i ,j对应的和等于上一层的和加上这一层累计的和
                sum[i][j]=s+sum[i-1][j];
                //System.out.print(sum[i][j]+" ");
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        return sum[row2+1][col2+1]-sum[row2+1][col1]-sum[row1][col2+1]+sum[row1][col1];
    }

}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * int param_1 = obj.sumRegion(row1,col1,row2,col2);
 */

 题目3：

560. 和为 K 的子数组labuladong 题解思路

给你一个整数数组 nums 和一个整数 k ，请你统计并返回该数组中和为 k 的连续子数组的个数。

 

示例 1：

输入：nums = [1,1,1], k = 2
输出：2

示例 2：

输入：nums = [1,2,3], k = 3
输出：2

 

提示：

• 1 <= nums.length <= 2 * 104
• -1000 <= nums[i] <= 1000
• -107 <= k <= 107

前缀和思路，感觉要超时，刚好过

class Solution {
    public int subarraySum(int[] nums, int k) {
        int n=nums.length;
        int[] presum=new int[n+1];
        for (int i=1;i<n+1;i++){
            presum[i]=presum[i-1]+nums[i-1];
        }
        int res=0;
        for(int i=1;i<n+1;i++){
            for(int j=1;j<=i;j++){
                if (presum[i]-presum[j-1]==k){
                    res++;
                }
            }
        }
        return res;
    }
}

哈希表优化

class Solution {
    public int subarraySum(int[] nums, int k) {
        int n=nums.length,sum=0;
        int res=0;
        Map<Integer,Integer> map=new HashMap<>();
        map.put(0,1);
        for (int i=0;i<n;i++){
            sum+=nums[i];
            if (map.containsKey(sum-k)){
                res+=map.get(sum-k);
            }
            map.put(sum,map.getOrDefault(sum,0)+1);
        }
        return res;
    }
}