丁小帅+2016012047+作业5

散列函数的应用及其安全性

本次作业为扩展有关散列函数安全性的知识扩展。

作业题目：散列函数的应用及其安全性。

内容要求：

  (1) 给出散列函数的具体应用。

  (2) 结合生日攻击、以及2004、2005年王晓云教授有关   MD5安全性和2017年google公司SHA-1的安全性，  说明散列函数的安全性以及目前安全散列函数的发  展。问题2的回答可以参考下面给出的第一个链接。

（3）结合md5算法中的选择前缀碰撞以及第二个链接中的 helloworld.exe和goodbyworld.exe两个可执行文件的 md5消息摘要值和两个文件的执行结果说明md5算法 在验证软件完整性时可能出现的问题。

       链接1：https://www.win.tue.nl/hashclash/

       链接2：http://www.win.tue.nl/hashclash/SoftIntCodeSign/

 

---

 

(1) 给出散列函数的具体应用。

首先给出散列函数的定义：

简单的说，hash函数就是把任意长的输入字符串变化成固定长的输出字符串的一种函数。输出字符串的长度称为hash函数的位数。

散列函数把消息或数据压缩成摘要，使得数据量变小，将数据的格式固定下来，比如我们自定义密码的存储。

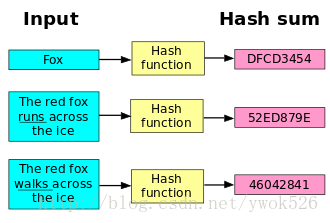
目前应用最为广泛的hash函数是SHA-1和MD5，大多是128位和更长。hash函数在现实生活中应用十分广泛。很多下载网站都提供下载文件的MD5码校验，可以用来判别文件是否完整，在一些BitTorrent下载中，软件将通过计算MD5检验下载到的文件片段的完整性。

具体应用：

1）文件校验

　　 我们比较熟悉的校验算法有奇偶校验和CRC校验，这2种校验并没有抗数据篡改的能力，它们一定程度上能检测并纠正数据传输中的信道误码，但却不能防止对数据的恶意破坏。

　　 MD5 Hash算法的"数字指纹"特性，使它成为目前应用最广泛的一种文件完整性校验和（Checksum）算法，不少Unix系统有提供计算md5 checksum的命令。

　　2）数字签名

　　 Hash 算法也是现代密码体系中的一个重要组成部分。由于非对称算法的运算速度较慢，所以在数字签名协议中，单向散列函数扮演了一个重要的角色。对 Hash 值，又称"数字摘要"进行数字签名，在统计上可以认为与对文件本身进行数字签名是等效的。而且这样的协议还有其他的优点。

　　3）鉴权协议

如下的鉴权协议又被称作"挑战--认证模式：在传输信道是可被侦听，但不可被篡改的情况下，这是一种简单而安全的方法。

（2）结合生日攻击、以及2004、2005年王晓云教授有关MD5安全性和2017年google公司SHA-1的安全性，说明散列函数的安全性以及目前安全散列函数的发展。

生日攻击：生日攻击就是利用散列函数发生碰撞的可能性，进行n次尝试直到找到一对碰撞的输入。一个40比特长的消息摘要是很不安全的，大约一百万次随机Hash可至少以50%的概率找到一个碰撞。

MD5加密代码demo：

package cn.itcast.estore.utils;

import java.math.BigInteger;
import java.security.MessageDigest;
import java.security.NoSuchAlgorithmException;

public class MD5Utils {
	/**
	 * 使用md5的算法进行加密
	 */
	public static String md5(String plainText) {
		byte[] secretBytes = null;
		try {
			secretBytes = MessageDigest.getInstance("md5").digest(
					plainText.getBytes());
		} catch (NoSuchAlgorithmException e) {
			throw new RuntimeException("没有md5这个算法！");
		}
		String md5code = new BigInteger(1, secretBytes).toString(16);// 16进制数字
		// 如果生成数字未满32位，需要前面补0
		for (int i = 0; i < 32 - md5code.length(); i++) {
			md5code = "0" + md5code;
		}
		return md5code;
	}

	public static void main(String[] args) {
		System.out.println(md5("123"));
	}

}

　　

2004、2005年王晓云教授有关MD5安全性中提到：

        安全的Hash函数在设计时必须满足的一个要求是寻找两个输入得到相同的输出值在计算上是不可行的，这就是我们通常所说的抗碰撞的。MD5就是这样一个在国内外有着广泛的应用的Hash函数算法，它曾一度被认为是非常安全的。然而，王小云教授发现，可以很快的找到MD5的“碰撞”，就是两个文件可以产生相同的“指纹”。这意味着，当你在网络上使用电子签名签署一份合同后，还可能找到另外一份具有相同签名但内容迥异的合同，这样两份合同的真伪性便无从辨别。

SHA-1：SHA-1是1995年国家标准技术局NIST（National Institute of Standards and Technology）于1995年标准化的哈希函数。与前身MD5相比，SHA-1的输出长度更长（MD5输出长度为128bit，而SHA-1的输出长度为160bit），这也意味着出现哈希碰撞的概率更低。同时，SHA-1的安全性似乎也比MD5更好。这里要稍微介绍一下寻找哈希函数碰撞的难度和一般方法了。以SHA-1为例，其哈希结果长度为160bit。如果SHA-1本身没有漏洞，而攻击者想找到一组碰撞的话，最显然的方法是选取组不同的数据，依次计算它们的哈希结果。根据著名的抽屉原理，必然会出现一组数据，使得其哈希结果相同。此攻击方法需要调用次SHA-1，即计算量级大约为。

2017年google公司SHA-1的安全性中提到：

        Google 的安全团队攻破了SHA-1安全加密算法。这次攻破被命名为 SHAttered attack。研究者提供了两张内容截然不同，在颜色上存在明显差异，但 SHA-1 哈希值却完全相同的 PDF 文件作为证明。哈希碰撞（hash collision，即两个不同文件哈希值一致，也有译作哈希冲突）本来不应该发生。但实际上，当哈希算法存在漏洞时，一个有足够实力的攻击者能够制造出碰撞。进而，攻击者可以用去攻击那些依靠哈希值来校验文件的系统，植入错误的文件造成恶果。

散列函数发展

 

2005年MD5的攻破似乎宣告了SHA或许为仅存的安全散列算法。

 

SHA-0：SHA由美国标准与技术研究所（NIST）设计并于1993年发表，该版本称为SHA-0，由于很快被发现存在安全隐患，

 

SHA-1：1995年发布了SHA-1。

 

SHA-2：2002年，NIST分别发布了SHA-256、SHA-384、SHA-512，这些算法统称SHA-2。2008年又新增了SHA-224。

 

由于2017年SHA-1算法的攻破，目前已经有多家科技企业宣布逐步放弃SHA-1算法，微软已经确定会放弃在Edge以及IE浏览器上继续使用SHA-1算法的TLS证书，Google的Chrome在56版之后也会提示SHA-1加密的HTTPS网页并不安全，Mozilla则确定在今年7月开始停止SHA-1的支持。目前SHA-2各版本已成为主流。

 

（3）结合md5算法中的选择前缀碰撞以及第二个链接中的helloworld.exe和goodbyworld.exe两个可执行文件的md5消息摘要值和两个文件的执行结果说明md5算法在验证软件完整性时可能出现的问题。

选择前缀碰撞

   通过选择不同的前缀，计算生日数和碰撞块添加到文件尾部，即可得到两个具有相同的MD5的文件。不过，要计算出这些尾部数据并不容易，直接使用hashclash[[1]]的工具需要相当大的时间成本，但是碰撞作者对该工具进行改进后已经能够高效完成大量正常程序与恶意程序的碰撞了，以下为此阶段样本的典型样例（每组正常程序与恶意程序对照），由于碰撞的原理与文件格式无关，所以样本形态呈现了多样化的特点。

可能出现的问题：我们为了保证消息的完整性，引进了散列函数，散列函数会对安全性造成影响。

三个概念：

1.如果y<>x，且h（x）=h（y），则称为碰撞。

2.对于给定的x，要找到一个y满足y<>x，h（x）=h（y），在计算上不可行，称为弱无碰撞。

3.要找到任意一对数，x，y，y<>x，满足h（x）=h（y），在计算上不可行，则称为强无碰撞。（包含弱无碰撞）

假定：一个取整数的随机变量，服从1到n的随机分布，一个含有k个这种变量的集合，至少有一对重复的概率记为P，P大于二分之一，求k的范围

解：对于h（x）=a（a为某个特定的值）的概率为1/n

　　对于h（x）<>a（a为某个特定的值）的概率为1-1/n

　　k个变量没有重复的概率为： =1(1-1/n) (1-2/n) (1-3/n)… [1-(k-1)/n]

　　至少一对重复的概率：P=1 – n!/[(n-k)!nk]

　　根据不等式：(1-x) ≤e-x (对于0 ≤ x ≤ 1)

　　P>1-e(-(k(k-1)/(2n))

　　设E=1-e(-(k(k-1)/(2n))

　　k约等于(2nln(1/(1-E))0.5

　　当E=0.5，k约等于1.18n0.5

一间屋子的人数必须达到多少人才能使其中两个生日相同的机会达到50%？

k=1.18 * 3650.5=23，仅需要23人

结论：对于长度为m位的散列码，共有2m个可能的散列码，k个输入值的集合中，若要使其中的任意两个输入x和y，有h（x）=h（y）的概率为0.5，只需k=2m/2

碰撞对于基于Hash的数字签名影响

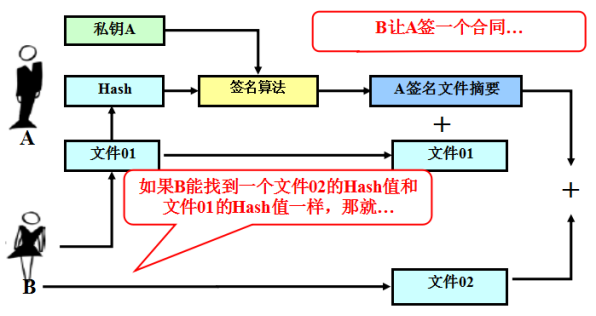
结果是A等于签了一份他根本不知道的文件02。

但是关键是找到一对想要的碰撞，因为文件02必须是有内容，并且是合乎语言语法的，因为就算找到一个文件02与文件01Hash值一样，文件02是无意义的，那么这样做也是毫无意义的！

在实例应用中，基本的Hash函数

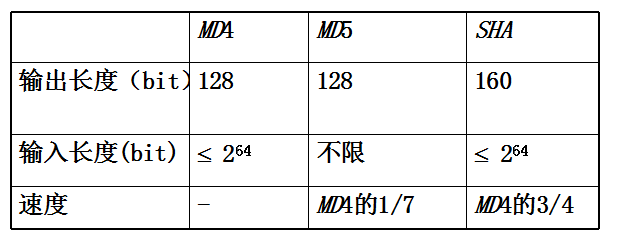
可以看到，经常使用的MD5，和SHA的输出长度分别是128和160，对于弱无碰撞性，被破解成功的可能性低于264和280！

结合第二个链接中的 helloworld.exe和goodbyworld.exe两个可执行文件的 md5消息摘要值和两个文件的执行结果

HelloWorld.exe   GoodbyeWorld.exe  这两个程序会在屏幕上打印出不同的字符，但是它们的MD5都是一致的。这几位密码学家使用的是“构造前缀碰撞法”（chosen-prefix collisions）来进行此次攻击。

参考博文：https://www.cnblogs.com/13jhzeng/p/5532630.html