线段树。
1,要给自己设定目标,阶段,否则。。
2,线段树和二分方法思想。
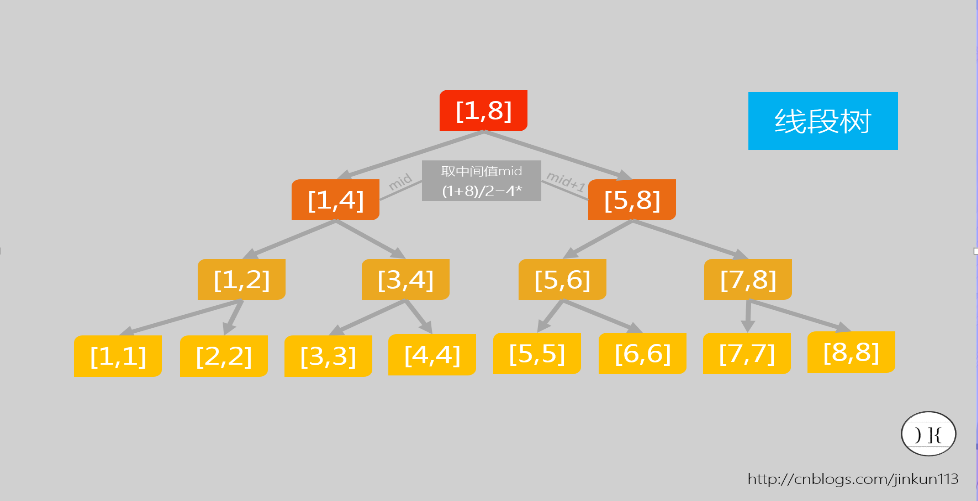
3.
4,
动态的维护一个前缀和
一个简单例题:
单点加,询问区间和
如果我们沿用之前的前缀和,每次询问之前都得把数组扫一遍,时间开销无法接受。
注意这个单点加,询问区间和什么的东西。
5,
啊记得要费曼。。
6,线段树预习
一,概念分为定义和基本使用方法
定义,线段树是一种二叉搜索树,与区间树类似,将一个区间分为一些单元区间,每个单元区间对应线段树中的一个节点。
使用,大家一般使用线段树来查询某节点在一些线段中的出现次数,时间复杂度为o(logN),空间复杂度为2N,不过一般会开到4N的数组以避免越界,有时还需要离散化以压缩空间。
二,基本代码框架和基本使用
用线段树来进行单点,区间的修改与查询。
(这个一般来说要久一点,准备三个不同版本的看吧,看三个还不懂就可以换个知识点,另有方法对这种东西
在看的同时往往我们会发下出现了许多可能不认识的名词,但是,但是我们不要去查,等整个地看完这个阶段,一个版本看完可以查
一个东西。不要什么不认识就去查什么。。这样。。不久dfs了吗。。。我他妈。。。这竟然都能和dfs联系起来。反正之前的经验你也懂你这种单纯地dfs容易tle噢。)
(判断自己专注可以根据这么两个东西,一个是呼吸,一个心中跟着默默念,毕竟这个东西都是要仔细理解地)
(对待这种抽象的sb,手中随时准备纸笔去算一遍。)
(看地时候脑海里主要做地事总结一下在说啥)
1,线段树最基本的操作为插入和删除一条线段。
2,记录线段是否被覆盖
我们可以定义一个int count来代表整个线段中被覆盖的长度,那么我们就需要在删除和插入线段中维护这个被覆盖的长度。
同理可以推断出的问题事
2.1判断一个节点或者一段线段是否被覆盖掉。
我们可以定义一个bool count,在插入和删除中维护这个bool值。
3,一具体问题:假设插入操作为每个节点的位置加k,那么查询操作为求整个线段长,且每个节点上的值为sum;
那么就会引起一个空间上的问题,每次插入操作我们都要对n个节点的值进行更新,那么时间复杂度事o(n)的。
在这里我们可以用lazy思想:对于整个节点的操作,我们不去立即执行加k操作,而是将此标记,等待其查询时再将操作分为两部分进行
具体来说,我们再不代表原线段的节点上定义一个toadd值,toadd值代表的要增加的k值的总和
百度上的沙雕
5,哭了(代码那行怎么都换行不下去)
①区间查询操作。
如有个数组A[100],求A[2]~A[50]...
若搜索的区间被目标区间完全覆盖,那么直接返回该搜索区间的值即可。
若搜索的区间和左儿子有交集,那么搜索左儿子。
若搜索的区间和右儿子有交集,那么搜索右儿子。
(说实话,抽象教学最后以实例来参考!)
(
我们想一种新的方法,先想一个比较好画图的数据,比如一个长度为4的区间,分别是1、2、3、4,我们想求出第1~3项的和。按照上一部说的,我们要建出一颗线段树,其中点权(也就是红色)表示和:

然后我们要求1~3的和,我们先从根节点开始查询,发现她的左儿子1~2这个区间和答案区间1~3有交集,那么我们跑到左儿子这个区间。
然后,我们发现这个区间1~2被完全包括在答案区间1~3这个区间里面,那就把她的值3返回。
我们回到了1~4区间,发现她的右儿子3~4区间和答案区间1~3有交集,那么我们走到3~4区间
到了3~4区间,我们发现她并没有完全包含在答案区间1~3里面,但发现她的左儿子3~3区间和1~3区间又交集,那么久走到3~3区间
到了3~3区间,发现其被答案区间完全包含,就返回她的值3一直到最开始
3~3区间的3+1~2区间的3=6,我们知道了1~3区间和为6.
有人可能会说你这样是不是疯了,我那脚都能算出1+2+3=6,为什么这么麻烦?!
因为这才几个数,如果一百万个数,这样时间会大大增快。
)抄别人的不好意思啊。
4,(百度百科上什么jb玩意)
1 inline void build(int i,int l,int r){//递归建树 2 tree[i].l=l;tree[i].r=r; 3 if(l==r){//如果这个节点是叶子节点 4 tree[i].sum=input[l]; 5 return ; 6 } 7 int mid=(l+r)>>1; 8 build(i*2,l,mid);//分别构造左子树和右子树 9 build(i*2+1,mid+1,r); 10 tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;//刚才我们发现的性质return ; 11 }
5,wocao
你基本的查询区间加和什么的都没有。
6,区间查询和单点修改操作
1 void search(int i,int l,int r) 2 { 3 if(tree[i].l>l1&&tree[i].r<r1) return tree[i].sum; 4 if(tree[i].r>l1||tree[i].l<r1) return 0; 5 int sumup=0; 6 //这种左右两边的挺容易弄错的。》 7 if(tree[i*2].r>=l) sumup+=search(i*2,l,r); 8 if(tree[i*2+1].l<=r) sumup+=search(i*2+1,l,r); 9 return sumup; 10 } 11 int add(int i,int dis,int k) 12 { 13 //第dis位加上一个k值 14 if(tree[i].l==tree[i].r){ 15 16 tree[i].sum+=k; 17 return;} 18 if(dis<=tree[i*2].r)//这块的查询有点像二分哪个意思 19 add(i*2,dis,k); 20 else 21 add(i*2+1,dis,k); 22 //下面这个是返回更新 23 tree[i].sum=tree[i*2].sum+tree[i*2+1].sum; 24 return ; 25 //真是越来越展示 了递归与return 之美 26 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号