1254. Number of Closed Islands

Given a 2D grid consists of 0s (land) and 1s (water).  An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.

Return the number of closed islands.

 

Example 1:

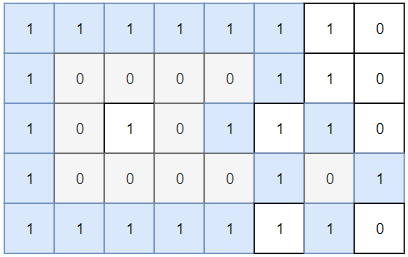
Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output: 2
Explanation: 
Islands in gray are closed because they are completely surrounded by water (group of 1s).

Example 2:

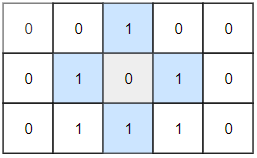
Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output: 1

Example 3:

Input: grid = [[1,1,1,1,1,1,1],
               [1,0,0,0,0,0,1],
               [1,0,1,1,1,0,1],
               [1,0,1,0,1,0,1],
               [1,0,1,1,1,0,1],
               [1,0,0,0,0,0,1],
               [1,1,1,1,1,1,1]]
Output: 2

class Solution {
    public int closedIsland(int[][] grid) {
        if (grid == null || grid.length == 0) return 0;
        int rows = grid.length;
        int cols = grid[0].length;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if ((i == 0 || j == 0 || i == rows - 1 || j == cols - 1) && grid[i][j] == 0) {
                    dfs(grid, i, j);
                }
            }
        }
        int count = 0;
        for (int i = 1; i < rows - 1; i++) {
            for (int j = 1; j < cols - 1; j++) {
                if (grid[i][j] == 0) {
                    dfs(grid, i, j);
                    count++;
                }
            }
        }
        return count;
    }
    
    private void dfs(int[][] grid, int i, int j) {
        int rows = grid.length;
        int cols = grid[0].length;
        if (i < 0 || i >= rows || j < 0 || j >= cols || grid[i][j] != 0) return;
        
        grid[i][j] = 1;
        dfs(grid, i - 1, j);
        dfs(grid, i + 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i, j - 1);
    }
}