1197. Minimum Knight Moves

In an infinite chess board with coordinates from -infinity to +infinity, you have a knight at square [0, 0].

A knight has 8 possible moves it can make, as illustrated below. Each move is two squares in a cardinal direction, then one square in an orthogonal direction.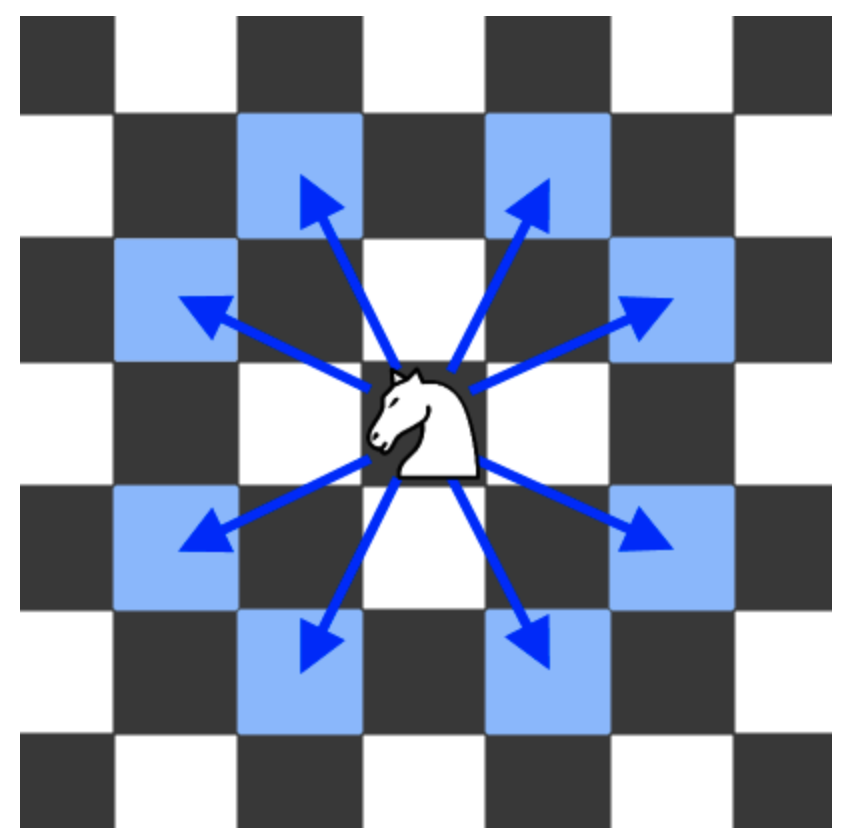

Return the minimum number of steps needed to move the knight to the square [x, y]. It is guaranteed the answer exists.

求最短路径，标准的bfs广度优先搜索题目。本题如果没有棋盘无限大这个条件，那么完完全全是一道简单的bfs模板题型。因此考虑到棋盘范围的因素，普通的bfs肯定会超时，所以我们应该首先确定下来从起点到终点的合理范围有哪些。显而易见，如果朝着终点越来越远的方向走肯定是浪费计算时间的部分，如果简单来为棋盘来划定一下界限，起点和终点两个坐标(x1,y1), (x2,y2)围成的四边形应该是相对合理的范围。但是考虑到如果两个点在一条直线上，或者两点间的距离过近而无法完成日字跳跃的情况，我们可以将划定的棋盘范围四周分别扩大2格即可。

此外，为了方便，我们可以将起点和终点平移到正数坐标范围内。举个例子，比如：

int x = -5; // 终点x

int y = -3; // 终点y

int startX = 0; // 起点x

int starty = 0; // 起点y

先将终点移动到(0, 0)，相应的起点会被移动到(5, 3)。此外，要考虑到上面提到的扩大2格的操作，因此，终点T应该是(2, 2)，起点S则是(7, 5)。相应的棋盘范围则是(0, 0) 到(9, 7)之间的范围，即下图蓝色区域。

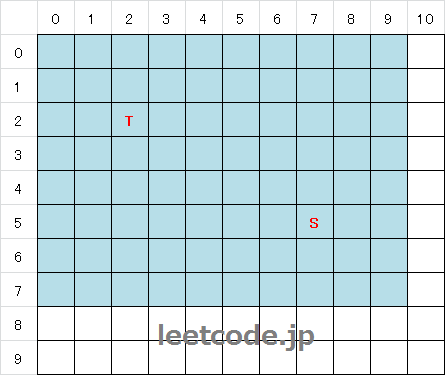
确定了棋盘范围之后，剩下的就是简单的常规bfs操作了。

class Solution {
    public int minKnightMoves(int x, int y) {
        // 定义bfs可以走的八个方向
        int[][] directions = { { -1, -2 }, { 1, -2 }, { 2, -1 }, { 2, 1 }, { 1, 2 }, { -1, 2 }, { -2, 1 }, { -2, -1 } };
        int startX = 0, startY = 0; // 起始坐标
        if (x < 0) { // 如果终点横坐标小于0
            // 起点横坐标与终点横坐标同时移动x个单位
            startX = -x;
            x = 0;
        }
        if (y < 0) { // 如果终点纵坐标小于0
            // 起点纵坐标与终点纵坐标同时移动y个单位
            startY = -y;
            y = 0;
        }
        // 为了将棋盘范围四周分别扩大2格，将起点和终点坐标再分别平移2个单位
        startX += 2;
        startY += 2;
        x += 2;
        y += 2;
        // 棋盘的右边界为起点和终点较大x值加2
        int right = Math.max(startX, x) + 2;
        // 棋盘的下边界为起点和终点较大y值加2
        int bottom = Math.max(startY, y) + 2;
        // 以下是常规bfs套路代码
        Queue<int[]> q = new LinkedList<>();
        q.offer(new int[] { startX, startY });
        boolean[][] visited = new boolean[right + 1][bottom + 1];
        visited[startX][startY] = true;

        int res = 0;
        while (q.size() > 0) {
            int size = q.size();
            while (size-- > 0) {
                int[] current = q.poll();
                if (current[0] == x & current[1] == y) {
                    return res;
                }
                for (int[] direction : directions) {
                    int nextX = current[0] + direction[0];
                    int nextY = current[1] + direction[1];
                    if (nextX <= right && nextX >= 0 && nextY <= bottom && nextY >= 0 && !visited[nextX][nextY]) {
                        visited[nextX][nextY] = true;
                        q.offer(new int[] { nextX, nextY });
                    }
                }
            }
            res++;
        }
        return -1;
    }
}

From: https://leetcode.jp/leetcode-1197-minimum-knight-moves-%e8%a7%a3%e9%a2%98%e6%80%9d%e8%b7%af%e5%88%86%e6%9e%90/