Dragon slayer

https://acm.hdu.edu.cn/showproblem.php?pid=7139
这道题写了快4个小时，一开始看错题浪费了一个多小时，然后重做又一堆bug，生生要把人气死。写个题解记录一下。

题目描述

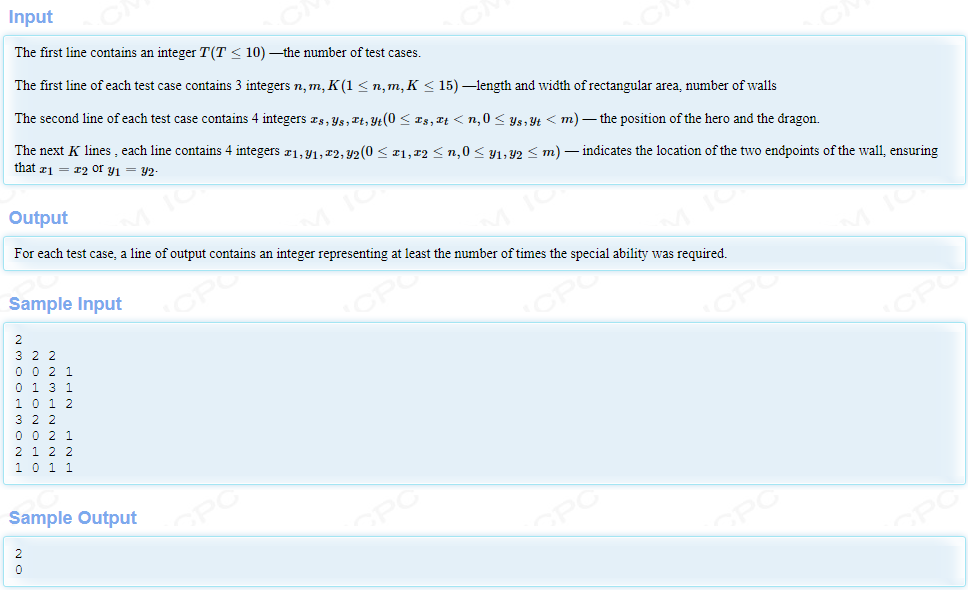
解题思路

注意到n,m,k的范围非常小，那么可以操作的空间就比较大。
一开始以为是最短路，但是每次运用能力可以消去一整堵强很不好处理，用最短路没法做。
于是考虑枚举，2的15次方大约在3e4左右。枚举所有剩余墙的组合，然后运用bfs判断英雄能否到达龙的位置就行了。最后取一个剩余墙最多，也就是运用能力次数最少的作为答案。
bfs大概复杂度在O(n*m),再乘个3e4，应该不会T。

代码

感觉自己的代码写的有点乱糟，不然也不会调了这么多次bug。。

#include <bits/stdc++.h>
using namespace std;

#define int long long

int mod = 1e9 + 7;

int n,m,K;

struct wall
{
    int x1,x2,y1,y2;
} w[20];     //作为墙的输入

bool ileg(int x,int y)
{
    if(x<0||x>=n||y<0||y>=m)
        return true;
    return false;
}
int dx[4] = {0,1,0,-1};
int dy[4] = {1,0,-1,0};

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);

    int xs,ys,xt,yt;

    int t;cin >> t;
    while(t--)
    {
        int ans = -1;    //记录最大剩余墙个数
        cin >> n >> m >> K;
        cin >> xs >> ys >> xt >> yt;
        for(int i=0;i<K;++i)
            cin >> w[i].x1 >> w[i].y1 >> w[i].x2 >> w[i].y2;
        for(int M=0;M<(1<<K);++M)    //枚举所有情况
        {
            //cout << 1 << endl;
            int tmp = 0;   //记录剩余墙的个数
            set<pair<int,int>> shu[16];   //竖着的墙
            set<pair<int,int>> heng[16];  //横着的墙
            for(int i=0;i<=K;++i)
            {
                if((1<<i)&M){    //墙被选中了
                    tmp++;
                    if(w[i].x1==w[i].x2)
                    {
                        shu[w[i].x1].insert({min(w[i].y1,w[i].y2),max(w[i].y1,w[i].y2)});
                    }
                    else{
                        heng[w[i].y1].insert({min(w[i].x1,w[i].x2),max(w[i].x1,w[i].x2)});
                    }
                }
            }
            //cout << "M " << M << endl;
            bool ok = 0;    //此情况是否合法

			//下面是bfs
            bool vis[16][16];
            memset(vis,0,sizeof vis);

            queue<pair<int,int>> q;
            q.push({xs,ys});
            vis[xs][ys] = 1;
            while(!q.empty())
            {
                pair<int,int> p = q.front();
                q.pop();
                //cout << p.first << " " << p.second << endl;

                if(p.first==xt&&p.second==yt)
                {
                    ok=1;
                    break;
                }

                for(int i=0;i<4;++i)
                {
                    int x = p.first + dx[i];
                    int y = p.second + dy[i];
                    if(ileg(x,y)) continue;
                    if(vis[x][y]) continue;
                    bool tiao = 0;
                    if(p.second==y)   //横着走是否有墙
                    {
                        int xx = x > p.first ? x : p.first;
                        if(!shu[xx].empty()){
                            for(auto l : shu[xx])
                                if(y>=l.first&&y<l.second)
                            {
                                tiao = 1;
                                break;
                            }
                        }
                        if(tiao) continue;
                    }
                    if(p.first==x)   //竖着走
                    {
                        int yy = y > p.second ? y : p.second;
                        if(!heng[yy].empty()){
                            for(auto l : heng[yy])
                                if(x>=l.first&&x<l.second)
                            {
                                tiao = 1;
                                break;
                            }
                        }
                        if(tiao) continue;
                    }
                    q.push({x,y});
                    vis[x][y] = 1;
                }
            }

            if(ok) ans = max(ans, tmp);
            //cout << ans << endl;
        }
        if(ans==-1) cout << -1 << endl;
        else cout << K - ans << endl;   //结果
    }

    return 0;
}
/*
3 2 2
2 1 0 0
0 1 3 1
1 0 1 2
*/