Chiitoitsu (期望dp)

https://ac.nowcoder.com/acm/contest/33186/I

解题思路：

令 \(f_{s,r}\) 表示剩余\(s\)张单牌、剩余\(r\)张可以摸的牌时的期望轮数。

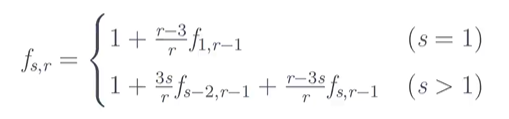
每次摸牌，回合数加1，这张牌可能可以凑成对子，也可能不行。凑成对子的概率是\(\frac{3s}{r}\)，否则是\(\frac{r-3s}{r}\)。凑成对子时，则剩下的回合数期望是\(f_{s-2,r-1}\)，否则是\(f_{s,r-1}\)。
通过dp来求。

代码

#include <bits/stdc++.h>
using namespace std;

#define int long long

int mod = 1e9 + 7;
int m = 4 * 34 - 13;

int pf(int x,int b)
{
    int res = 1;
    while(b>0)
    {
        if(b&1) res = res * x % mod;
        x = x * x % mod;
        b >>= 1;
    }
    return res;
}

int dp[20][400];
void init()
{
    dp[1][3] = 1;
    for(int i=4;i<=m;++i)
    {
        dp[1][i] = (1 + (i-3) * pf(i, mod-2) % mod * dp[1][i-1] % mod) % mod;
    }
    for(int i=3;i<=13;i+=2)
        for(int j=3*i;j<=m;++j)
    {
        dp[i][j] = (1 + 3*i*pf(j,mod-2) % mod * dp[i-2][j-1] + (j-3*i)*pf(j,mod-2) % mod * dp[i][j-1] % mod) % mod;
    }
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);

    init();

    int t;cin >> t;
    int cas = 0;
    while(t--)
    {
        string s;
        cin >> s;
        set<string> se;
        for(int i=0;i<(int)s.length();i+=2)
        {
            string t = s.substr(i,2);
            if(se.count(t)) se.erase(t);
            else se.insert(t);
        }
        int k = se.size();

        cout << "Case #"<< ++cas <<": " << dp[k][m] << endl;
    }

    return 0;
}