最大公共子序列、子串、可重叠重复子串
最长公共子序列
寻找两个给定序列的子序列,该子序列在两个序列中以相同的顺序出现,但是不必要是连续的
举例:X=ABCBDAB,Y=BDCABA。序列 BCA是X和Y的一个公共子序列,但不是X和Y的最长公共子序列,子序列BCBA是X和Y的一个LCS,序列BDAB也是
解法:动态规划是为了降低时间复杂度的一种算法,申请一个额外空间,来保存每一个步骤的结果,最后从这些结果中找到最优的解。一般来说,当前的最优解,只与当前时刻和上一时刻有关系,和其他时刻没有关系,这样才能让动态规划发生作用,降低复杂度。(DP动态规划最终处理的还是数值(极值做最优解),找到了最优值,就找到了最优方案)。
定义dp[i][j]记录序列LCS的长度,用i和j分别表示序列X的长度和序列Y的长度,状态转移方程为
- dp[i][j] = 0 如果i=0或j=0
- dp[i][j] = dp[i-1][j-1] + 1 如果X[i-1] = Y[i-1]
- dp[i][j] = max{ dp[i-1][j], dp[i][j-1] } 如果X[i-1] != Y[i-1]
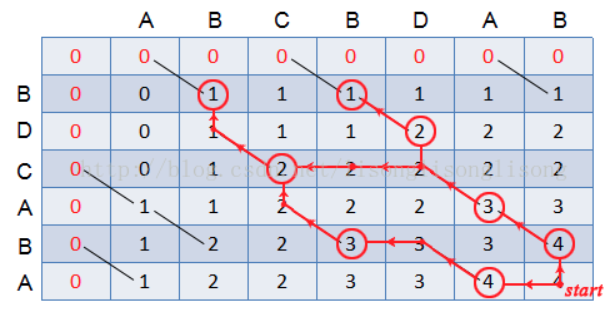
动态规划和滚动数组优化空间。
解法:动态规划dp解法:空间和时间O(m*n)
#include <vector> #include <set> #include <string> #include <iostream> #include <sstream> using namespace std; set<string> all_lcs; //注意这里要用set去除重复的LCS
//二维数组veca[i][j]记录的是两个字符串Xi和Yj的LCS长度 int LCS_length(const string &str1, const string &str2, vector<vector<int> > &veca) { int i, j; if (str1 == "" || str2 == "") return 0; for (i = 0; i <= str1.length(); i++) {//侧面的一行和一列初始化为0 veca[i][0] = 0; } for (j = 0; j <= str2.length(); j++) { veca[0][j] = 0; } for (i = 1; i <= str1.length(); i++) { for (j = 1; j <= str2.length(); j++) { if (str1[i - 1] == str2[j - 1]) { veca[i][j] = veca[i - 1][j - 1] + 1; } else { if (veca[i - 1][j] >= veca[i][j - 1]) veca[i][j] = veca[i - 1][j]; else veca[i][j] = veca[i][j - 1]; } } } return veca[str1.length()][str2.length()]; } //该函数找出所有的LCS的序列,并将其存在vector中 void PrintAllLCS(string &str1, string &str2, int i, int j, vector<vector<int> > &veca, string lcs_str) { //注意这里形参lcs_str不可以为引用,这里需要每次调用lcs_str都重新生成一个对象 while (i > 0 && j > 0) { if (str1[i - 1] == str2[j - 1]) { lcs_str = str1[i - 1] + lcs_str; //逆向存放 --i; --j; } else { if (veca[i - 1][j] > veca[i][j - 1]) //向左走 --i; else if (veca[i - 1][j] < veca[i][j - 1]) //向上走 --j; else { //此时向上向右均为LCS的元素 PrintAllLCS(str1, str2, i - 1, j, veca, lcs_str); PrintAllLCS(str1, str2, i, j - 1, veca, lcs_str); return; } } } cout << " " << lcs_str << endl; all_lcs.insert(lcs_str); } int main() { string input; getline(cin, input);//读入一行,默认遇到\n回车时停止 stringstream ss(input); string str1, str2; ss >> str1;//遇到空格停止 ss >> str2; //空格后赋值给str2 //将veca初始化为一个二维数组,其行列值分别为str1和str2的长度加1 //二维数组veca记录的是两个字符串Xi和Yj的LCS长度 vector<vector<int> > veca(str1.length() + 1, vector<int>(str2.length() + 1)); cout << LCS_length(str1, str2, veca) << endl; //输出 string lcs_str; PrintAllLCS(str1, str2, str1.length(), str2.length(), veca, lcs_str); set<string>::iterator iter = all_lcs.begin(); while (iter != all_lcs.end()) { cout << *iter++ << endl; } return 0; }
2、优化:滚动数组
优化空间变O(N),时间还是O(m*n),但此时无法输出子序列
#include <vector> #include <set> #include <string> #include <iostream> #include <sstream> using namespace std; //二维数组veca[i][j]记录的是两个字符串Xi和Yj的LCS长度 int LCS_length(const string &str1, const string &str2, vector<vector<int> > &veca) { int i, j; if (str1 == "" || str2 == "") return 0; //侧面的一行和一列初始化为0 veca[1][0] = 0; for (j = 0; j <= str2.length(); j++) { veca[0][j] = 0; } int k = 0; for (i = 1; i <= str1.length(); i++) { k = i & 1; for (j = 1; j <= str2.length(); j++) { if (str1[i - 1] == str2[j - 1]) { veca[k][j] = veca[k^1][j - 1] + 1; } else { if (veca[k^1][j] >= veca[k][j - 1]) veca[k][j] = veca[k^1][j]; else veca[k][j] = veca[k][j - 1]; } } } return veca[k][str2.length()]; } int main() { string input; getline(cin, input);//读入一行,默认遇到\n回车时停止 stringstream ss(input); string str1, str2; ss >> str1;//遇到空格停止 ss >> str2; vector<vector<int> > veca(2, vector<int>(str2.length() + 1)); //只有2行,交替存储 cout << LCS_length(str1, str2, veca) << endl; return 0; }
最长公共子串
子串需要连续
dp[i][j]表示以x[i]和y[j]结尾的最长公共子串的长度。
因为要求子串连续,所以对于X[i]与Y[j]来讲,它们要么与之前的公共子串构成新的公共子串;要么就是不构成公共子串。故状态转移方程
- X[i] == Y[j],dp[i][j] = dp[i-1][j-1] + 1
- X[i] != Y[j],dp[i][j] = 0
对于初始化,i==0或者j==0,如果X[i] == Y[j],dp[i][j] = 1;否则dp[i][j] = 0。
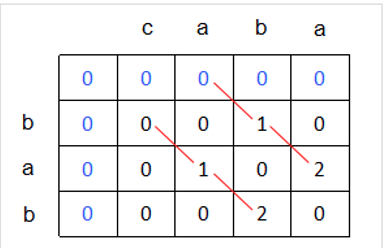
解法:动态规划、滚动数组优化空间、后缀数组优化时间和空间
1、输出多个最长公共子串
dp方法,时间空间都是O(m*n)。
2、优化
可按照最长公共子序列方法引入滚动数组优化空间On,但此时无法输出具体子串。
#include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> using namespace std; int maxindex[30]; int maxlen; /* 记录最大公共子串长度 */ //int maxindex; /* 记录最大公共子串在串1的起始位置 */ void outputLCS(char * X) { if (maxlen == 0) { printf("NULL LCS\n"); return; } printf("The len of LCS is %d\n", maxlen); int i = 0; while (maxindex[i] != 0) { int k = maxlen; while (k--) { printf("%c", X[maxindex[i]++]); } printf("\n"); i++; } } int dp[30][30]; void LCS_dp(char * X, int xlen, char * Y, int ylen) { //maxlen = maxindex = 0; int k = 0; for (int i = 0; i < xlen; ++i) { for (int j = 0; j < ylen; ++j) { if (X[i] == Y[j]) { if (i && j) { dp[i][j] = dp[i - 1][j - 1] + 1; } if (i == 0 || j == 0) { dp[i][j] = 1; } if (dp[i][j] > maxlen) { maxlen = dp[i][j]; memset(maxindex, 0, 30); k = 0; maxindex[k++] = i + 1 - maxlen; } else if (dp[i][j] == maxlen) { maxindex[k++] = i + 1 - maxlen; } } } } outputLCS(X); } void main() { char X[] = "aaababbb"; char Y[] = "abadbbb"; /* DP算法 */ LCS_dp(X, strlen(X), Y, strlen(Y)); }
3、优化:后缀数组
字符串X的长度为m,Y的长度为n,最长公共子串长度为l,时间复杂度为O((m+n)*l*lg(m+n)),空间复杂度为O(m+n)
思路:由于后缀数组最典型的是寻找一个字符串的重复子串,所以,对于两个字符串,我们可以将其连接到一起,如果某一个子串s是它们的公共子串,则s一定会在连接后字符串后缀数组中出现两次,这样就将最长公共子串转成最长重复子串的问题了
注意:在找到两个重复子串时,不一定就是X与Y的公共子串,也可能是X或Y的自身重复子串,故在连接时候我们在X后面插入一个特殊字符‘#’,即连接后为X#Y。
注意:要保证找到公共子串后二者只有一个#号,这样才表示来自不同的字符串
后缀数组输出多个最长公共子串
#include<cstdio> #include<cstdlib> #include<cstring> #include<iostream> using namespace std; int maxlen; /* 记录最大公共子串长度 */ //int maxindex; /* 记录最大公共子串在串1的起始位置 */ int suff_index_vec[100]; char * suff[100]; void outputLCS() { if (maxlen == 0) { printf("NULL LCS\n"); return; } printf("The len of LCS is %d\n", maxlen); int i = 0; int j = 0; while (suff_index_vec[i++] != 0) { int k = maxlen; while (k--) { printf("%c", suff[suff_index_vec[i]][j++]);//针对某一个后缀字符串,从头开始输出maxlen个 } printf("\n"); } } //char * suff[100]; int pstrcmp(const void *p, const void *q) { return strcmp(*(char**)p, *(char**)q); } int comlen_suff(char * p, char * q) { //要保证找到公共子串后二者只有一个#号,这样才表示来自不同的字符串 int len = 0; while (*p && *q && *p++ == *q++) { ++len; if (*p == '#' || *q == '#') { //遇到#需要break,否则就是同一(连接的后一个)字符串内匹配 break; } } int count = 0; while (*p) { if (*p++ == '#') { ++count; break; } } while (*q) { if (*q++ == '#') { ++count; break; } } if (count == 1) //只有一个#,说明一个后缀在#前,一个后缀在#后 return len; return 0; } void LCS_suffix(char * X, int xlen, char * Y, int ylen) { int len_suff = xlen + ylen + 1; char * arr = new char[len_suff + 1]; /* 将X和Y连接到一起 */ strcpy(arr, X); arr[xlen] = '#'; strcpy(arr + xlen + 1, Y); for (int i = 0; i < len_suff; ++i) /* 初始化后缀数组 */ { suff[i] = &arr[i]; } qsort(suff, len_suff, sizeof(char *), pstrcmp); //int suff_index_vec[100]; int k = 0; for (int i = 0; i < len_suff - 1; ++i) { int len = comlen_suff(suff[i], suff[i + 1]); if (len > maxlen) { maxlen = len; memset(suff_index_vec, 0, 100); k = 0; suff_index_vec[k++] = i; //suf_index = i; } else if (len == maxlen) { suff_index_vec[k++] = i; } } outputLCS(); } void main() { char X[] = "aaababbb"; char Y[] = "abaebbb"; /* 后缀数组方法 */ LCS_suffix(X, strlen(X), Y, strlen(Y)); }
bnanana的最长可重叠重复子串Longest Repeat Substring是ana。
解法:基本方法和后缀数组优化空间和时间
以下都只输出一个。
1、基础方法
时间On2
#include<cstdio> #include<string> using namespace std; int maxlen; /* 记录最长重复子串长度 */ int maxindex; /* 记录最长重复子串的起始位置 */ int comlen(char * p, char * q) { //比较重叠长度。输入是指针,然后对字符串顺序比对 int len = 0; while (*p && *q && *p++ == *q++) { ++len; } return len; } void outputLRS(char * arr) { //输出 if (maxlen == 0) { printf("NULL LRS\n"); return; } printf("The len of LRS is %d\n", maxlen); int i = maxindex; while (maxlen--) { printf("%c", arr[i++]); } printf("\n"); } void LRS_base(char * arr, int size) { for (int i = 0; i < size; ++i) { for (int j = i + 1; j < size; ++j) { int len = comlen(&arr[i], &arr[j]); if (len > maxlen) { maxlen = len; maxindex = i; } } } outputLRS(arr); } void main() { char X[] = "banana"; /* 基本算法 */ LRS_base(X, strlen(X)); }
2、优化:后缀数组
时间On
#include<cstdio> #include<string> using namespace std; int maxlen; /* 记录最长重复子串长度 */ int maxindex; /* 记录最长重复子串的起始位置 */ int comlen(char * p, char * q) { //比较重叠长度。输入是指针,然后对字符串顺序比对 int len = 0; while (*p && *q && *p++ == *q++) { ++len; } return len; } void outputLRS(char * arr) { //输出 if (maxlen == 0) { printf("NULL LRS\n"); return; } printf("The len of LRS is %d\n", maxlen); int i = maxindex; while (maxlen--) { printf("%c", arr[i++]); } printf("\n"); } char * suff[30]; //数组元素都是指针 int pstrcmp(const void * p, const void * q) {//p指向suff[0],需要先char**让suff[0]指向是char,然后*取suff[0]的值,即一个指针 return strcmp(*(char**)p, *(char**)q); //p大,返回大于0,则需要交换 } void LRS_suffix(char * arr, int size) { int suff_index = maxlen = maxindex = 0; for (int i = 0; i < size; ++i) /* 初始化后缀数组,每个里面放arr元素一个指针*/ { suff[i] = &arr[i]; } qsort(suff, size, sizeof(char *), pstrcmp); /* 字典序排序后缀数组 */ for (int i = 0; i < size - 1; ++i) /* 寻找最长重复子串 */ { int len = comlen(suff[i], suff[i + 1]); if (len > maxlen) { maxlen = len; suff_index = i; } } outputLRS(suff[suff_index]); } void main() { char X[] = "banana"; /* 后缀数组方法 */ LRS_suffix(X, strlen(X)); }
其中字典序排序结束的后缀数组suff:
suff[0] a
suff[1] a 但放入comlen中会*p++,即为ana
suff[2] anana
suff[3] banana
suff[4] na
suff[5] nana




