进制与转换
进制与转换
1、为什么要使用进制数?
数据在计算机中的表示,最终以二进制的形式存在,就是像<黑客帝国>电影中那些0101010...的数字。
我们操作计算机,实际就是使用程序和软件在计算机上各种读写数据。
如果我们直接操作二进制的话,面对这么长的数进行思考或操作,没有人会喜欢。
用16进制或8进制可以解决这个问题。
因为,进制越大,数的表达长度也就越短。
之所以使用16或8进制,而不其它的,诸如9或20进制。是因为2、8、16, 分别是2的1次方、3次方、4次方。 这一点使得三种进制之间可以非常直接地互相转换。
8进制或16进制既缩短了二进制数,还能保持了二进制数的表达特点。转换还方便。
现在2进制、16进制比较常见,8进制在逐渐淘汰。
2、进制的介绍
- 10进制
我们最熟悉的10进制,就是用0~9的数表示逢10进1。 - 16进制
如果是16进制,它就是由0-9,A-F组成,与10进制的对应关系是:0-9 对应0-9;A-F对应10-15。(字母不区分大小写) - 2进制和8进制
2进制由0和1组成,逢2进1,例如2进制数:10,用10进制表达为:2
8进制由0~7组成,逢8进1,例如8进制数:10,用10进制表达为:8
二进制数,前缀是0b;八进制数,前缀是0o;十六进制数,前缀是0x
3、二进制与十进制之间的转换
3.1、十进制转二进制
方法为:十进制数除2取余法,即十进制数除2,余数为权位上的数,得到的商值继续除2,依此步骤继续向下运算直到商为0为止。

3.2、二进制转十进制
方法一为:把二进制数按权展开、相加即得十进制数。
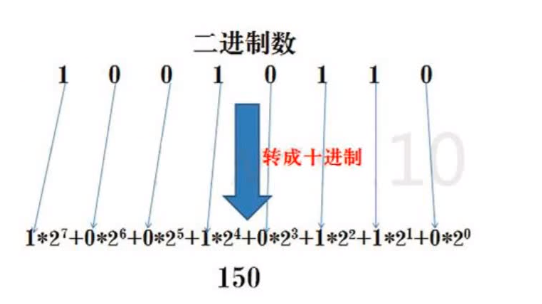
方法二:举证,把最高位逐一往低位强行进行降位。
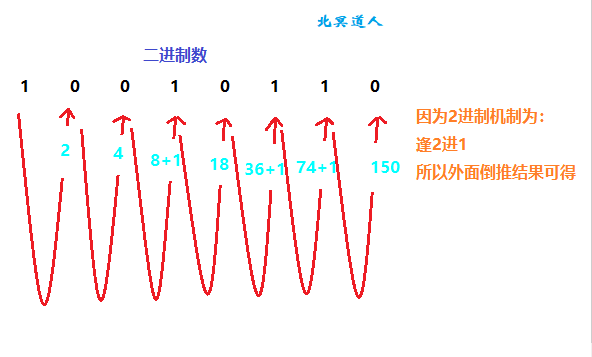
(额,图片丑了点,嘿嘿)
3.3、十进制小数转二进制
十进制小数转换成二进制小数采用 “乘2取整,顺序排列” 法。具体做法是:
用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数 部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来,先取的整数作为二进制小数的高位有效位,后取的整数作为低位有效位。
4、二进制与十六进制之间的转换
4.1、二进制转十六进制
方法:十六进制是取四合一,从右往左,每4个一组提出来,用二进制转十进制方法进行转换,最后连接每组。
注意事项:4位二进制转成十六进制是从右到左开始转换,不足时补0。最右边数0-9 对应0-9;A-F对应10-15。
4.2、十六进制转二进制
方法:十六进制也是取一分四,从右往左,每4个一组提出来,用十进制转二进制方法进行转换,最后连接每组。
5、补码
正数的补码和它的原码的形式是相同的。
负数的补码形式:将该数值的绝对值的二进制形式,按位取反为反码后,再加1。
为什么使用补码的形式来将数据存放在计算机底层:
使用补码,就可以把减法运算转换为加法,也就是说在计算机底层本质上没有减法是硬件实现,都是加法,降低硬件的设计难度,易于实现!
分析-下为什么用补码:
假设字长为8blts
完成 1-1 =0:
1 - (1) = 1 + (-1) = (00000001) + (10000001) --------原码计算 = (10000010) = (-2 )
完成 1-2 =-1:
1 - 2= 1 + (-2) = (0000001) + (10000010) -------原码计算 = (10000011) = (-3)
显然使用原吗计算时减法时,结果不对。
那使用反码呢?
完成 1-1 =0:
1 - 1
= 1 + (-1) = (00000001)+ (1111110) ---反码计算 = (11111111) = (10000000) ---转换原码 = (-0) ---有问题
完成 1-2 =-1:
1 - 2
= 1 + (-2) = (00000001) + (11111101) ---反码计算 = (11111110) = (10000001) ---转换原码 = (-1) ---正确.
问题出现在(+0)和(-0)上,在人们的计算概念中零是没有正负之分的,于是就引入了补码概念。
负数的补码
负数的补码就是对反码加1,而正数不变,正数的原码反码补码是一样的。
(-1) = (10000001)原码 = (11111110)反码 = ((11111110) + 1)补码
下面是补码的运算:
完成 1-1 =0:
1 - 1 = 1 + (-1) = (00000001)补 + (11111111)补 即:(11111110)+1)(反码加1) = (00000000)补 = (00000000)原 = 0 ---正确
完成 1-2 =-1:
1 - 2 = 1 + (-2) = (00000001)补+ (11111110)补 = (11111111)补 = (-1 ) ---正确
补码的设计目的是:
使符号位能与有效值部分一起参加运算,从而简化运算规则。
使减法运算转换为加法运算,进一步简化计算机中运算器的线路设计,所有这些转换都是在计算机的最底层进行的,而在我们使用的汇编、C等其他高级语言中使用的都是原码。

