四舍五入VS银行家舍入

相信细心的程序员们早就发现了.net环境下默认舍入算法的是“四舍六入”的算法。从小学我们就学过“四舍五入”算法，但是更加科学的舍入办法应该是“四舍六入”，也就是今天我们要讨论的“银行家舍入”。

大家可以做一个Demo。

C#环境下

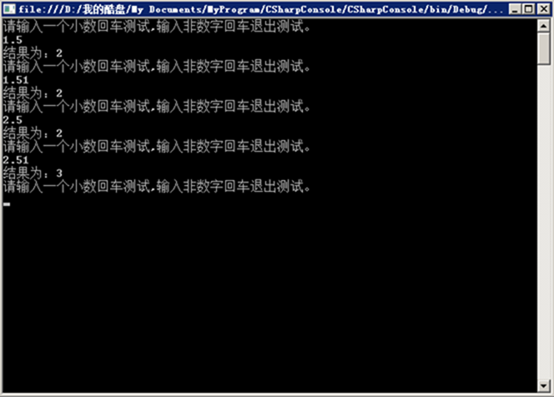
class Program
    {
        static  void Main(string[] args)
        {
           do
           {
                Console.WriteLine("请输入一个小数回车测试，输入其他回车结束测试");
                string Num = Console.ReadLine();
                try
                {
                    Console.WriteLine("结果为" + Convert.ToInt16(Convert.ToDouble(Num)));
                }
                catch (Exception e) {
                    break;
                }
           }
           while (true );
        }
    }

得到的结果如下

VB.net环境下测试代码为

    Sub Main()
        Do
            Console.WriteLine("请输入一个小数回车测试，输入其他回车结束测试。")
            Try
                Dim a As String = Console.ReadLine()
                Console.WriteLine("结果为：" & CInt(Convert.ToDouble(a)))
            Catch ex As Exception
                Exit Sub
            End Try
        Loop
    End Sub

结果如下

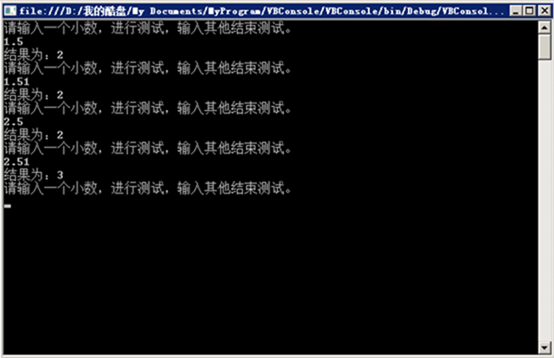
完全符合银行家舍入的规律：四舍六入五考虑，五后非零就进一，五后为零看奇偶，五前为偶应舍去，五前为奇要进一

关于VB.net中的CInt微软的MSDN上有具体说明

Fractional Parts. When you convert a nonintegral value to an integral type, the integer conversion functions ( CByte, CInt, CLng, CSByte, CShort, CUInt, CULng, and CUShort) remove the fractional part and round the value to the closest integer.

If the fractional part is exactly 0.5, the integer conversion functions round it to the nearest even integer. For example, 0.5 rounds to 0, and 1.5 and 2.5 both round to 2. This is sometimes called banker's rounding, and its purpose is to compensate for a bias that could accumulate when adding many such numbers together.

 

相对于四舍五入，银行家舍入的确更加的准确，讨论如下：

有些童鞋可能认为在一般性的测量中，最后一位小数位上0至9出现的概率是相等的。一共十个数字，0至4可以舍去（四舍），5至9可以进位（五入），多么完美的舍入算法！

但是！您可能忽略了一点，末尾的0在这里是相当于10还是相当于0？

为了避免混沌，请看下图：

图中是用Matlab画的一个简单的数轴，可以看出0.0、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0中0.0和1.0都是0结尾所以不能确定测量数据中的0是哪个零！

还是看上图，图中只要不满0.5都按照0算，大于0.5都按照1.0算，那么剩下的0.5怎么办？为了体现平均性，看上一位是奇数还是偶数，如果是奇数则进位，如果是偶数则舍去。这正是“银行家舍入”的思想。这样一来便达到了相对于“四舍五入”舍入方法更加平衡的舍入算法。

PS：“银行家舍入”是 IEEE 规定的舍入标准。因此所有符合 IEEE 标准的语言都是采用这一算法的。