快速排序

算法概述：

与归并排序一样，快速排序也是基于分治思想的一种应用。对于包含n个数的输入数组来说，快速排序是一种最坏情况时间复杂度为O(n²)的排序算法。虽然最坏情况时间复杂度很差，但是快速排序通常是实际排序应用中最好的选择，因为它的平均性能非常好：它的期望时间是O(nlgn)且隐含的常数因子非常小，能够进行原址排序，甚至在虚存环境也能很好的工作。

算法步骤：

1、分解。从数组中，选择一个元素作为基准，将数组中小于基准元素的排到基准之前，大于的排到基准之后；

2、递归。分别递归排序较大元还给的子数组与较小的元素的子数组，直至为0或一个元素，即不需要排序；

3、因为子数组都是原址排序，不需要进行合并；

示意图：

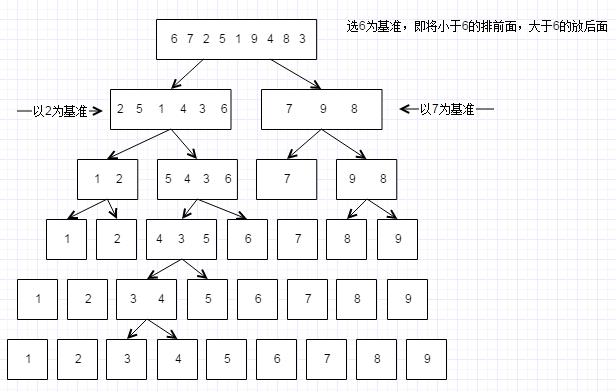
上图切分是原地切分，需要一个辅助数组，但切分后将辅助数组复制回原数组会有开销，所以一般采用下面这种切分方式：

c#代码实现：(非原地切分)

public class quick
    {
        public int[] a = { 6, 7, 2, 5, 1, 9, 4, 8, 3 };
        public void Sort()
        {
            Sort(a, 0, a.Length - 1);
        }
        public void Sort(int[] a, int low, int high)
        {
            if (high <= low) return;
            int mid = splitSort(a, low, high);
            Sort(a, low, mid - 1);
            Sort(a, mid + 1, high);
        }
        public int splitSort(int[] a, int low, int high)
        {
            int v = a[low];
            int i = low;
            int j = high + 1;
            while (true)
            {
                while (a[++i] < v && i < high);
                while (a[--j] > v && j > 0) ;
                if (i >= j) break;
                int temp = a[i];
                a[i] = a[j];
                a[j] = temp;
            }
            int temp1 = a[low];
            a[low] = a[j];
            a[j] = temp1;
            return j;
        }
            }

erlang代码实现：

sort([]) ->
    [];
sort(List) when is_list(List) ->
    sort2(List).

sort2([]) ->
    [];
sort2([Value | List]) ->
    {LeftList, RightList} = spilt_sort(List, Value, [], []),
    sort2(LeftList) ++ [Value]++ sort2(RightList).

spilt_sort([], _Value, LeftAcc, RightAcc) ->
    {LeftAcc, RightAcc};
spilt_sort([H | List], Value, LeftAcc, RightAcc) when H > Value ->
    spilt_sort(List, Value, LeftAcc, [H | RightAcc]);
spilt_sort([H | List], Value, LeftAcc, RightAcc) ->
    spilt_sort(List, Value, [H | LeftAcc], RightAcc).