归并排序是基于分治策略思想的一种典型有效的排序算法;
算法步骤:
1、将n个元素的原数组划分成只有一个元素的子数组,因为子数组只有一个元素则可以将子数组视为有序数组;
2、两两进行合并,由小到大将元素复制到临时数组中,复制完成后临时数组回写到原数组;
3、重复2步骤;
稳定性:稳定排序
因为划分时是按顺序来划分的,当两个元素相等时必然也是按顺序抄写到临时数组上的;
算法复杂度:nlogn
则于递归划分子数组只需要lgN复杂度,而合并每两个子序列需要2n次赋值(按序抄写到临时数组、回写原数组),为O(n)复杂度,因此事归并排序的时间复杂度为O(nlgn)。因为需要临时数组,所以空间复杂度为O(n);
归并排序步骤示意图:
1、将原数据划分成n个元素为1的子数组
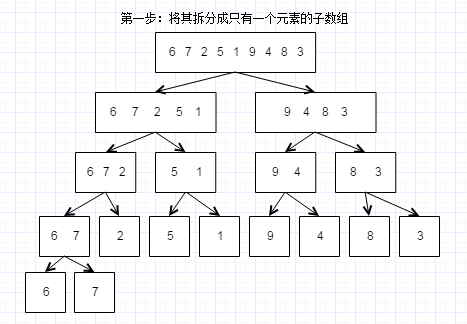
2、将划分好的子数组按划分时的倒序,将元素排序合并

两个子数组进行排序合并的具体流程

c#代码实现:
public class Merge { int[] a = { 12, 454, 1, 44, 33, 0, 85, 41, 87, 26, 6, 7, 80, 32, 12, 15 }; public void mergeSort() { int[] temp = new int[a.Length]; splitMergeSort(a, temp, 0, a.Length - 1); } public void splitMergeSort(int[] a, int[] temp, int left, int right) { if (left < right) { int mid = (left + right) / 2; splitMergeSort(a, temp, left, mid); splitMergeSort(a, temp, mid + 1, right); mergeSortArr(a, temp, left, mid, right); } } public void mergeSortArr(int[] a, int[] temp, int left, int mid, int right) { int k = 0; int i = left; int j = mid + 1; while (i <= mid && j <= right) // 左右两个子数组都有元素时,从小到大复制到临时数组 { if(a[i] <= a[j]) { temp[k++] = a[i++]; } else { temp[k++] = a[j++]; } } while (i <= mid) // 只有左子数组有元素时,将元素全部复制到临时数组 { temp[k++] = a[i++]; } while (right >= j) // 只有右子数组有元素时,将元素全部复制到临时数组 { temp[k++] = a[j++]; } for (int t = 0; t < k; t++) { a[left + t] = temp[t]; } } }
erlang 代码实现:
merge_sort([]) -> []; merge_sort([H]) -> [H]; merge_sort(List) -> Mid = erlang:length(List) div 2, {Left, Right} = lists:split(Mid, List), L = merge_sort(Left), R = merge_sort(Right), merge(L, R, []). merge([], [], Acc) -> lists:reverse(Acc); merge([], [H2 | L2], Acc) -> merge([], L2, [H2 | Acc]); merge([H1 | L1], [], Acc) -> merge(L1, [], [H1 | Acc]); merge([H1 | L1], [H2 | L2], Acc) when H1 =< H2 -> merge(L1, [H2 | L2], [H1 | Acc]); merge([H1 | L1], [H2 | L2], Acc) -> merge([H1 | L1], L2, [H2 | Acc]).
erlang 代码tuple模拟实现数组方式实现(相当于上面c#实现的erlang版本,较上面erlang的实现性能会比较低):
test_merge_sort(List) -> Tuple = erlang:list_to_tuple(List), merge_sort(Tuple, 1, length(List), Tuple). merge_sort(Tuple, Left, Right, TupleAcc) when Left < Right -> Mid = (Left + Right) div 2, Tuple1 = merge_sort(Tuple, Left, Mid, TupleAcc), Tuple2 = merge_sort(Tuple1, Mid + 1, Right, TupleAcc), merge(Tuple2, Left, Mid, Right, Left, Mid + 1, []); merge_sort(Tuple, _Left, _Right, _TupleAcc) -> Tuple. %% 将两个子序列元素进行比较,从小到大插入到临时列表中 merge(Tuple, Left, Mid, Right, LeftAcc, MidAcc, TempAcc) when LeftAcc =< Mid andalso MidAcc =< Right -> LeftValue = element(LeftAcc, Tuple), RightValue = element(MidAcc, Tuple), case LeftValue =< RightValue of true -> merge(Tuple, Left, Mid, Right, LeftAcc + 1, MidAcc, [LeftValue | TempAcc]); _ -> merge(Tuple, Left, Mid, Right, LeftAcc, MidAcc + 1, [RightValue | TempAcc]) end; merge(Tuple, Left, Mid, Right, LeftAcc, MidAcc, TempAcc) when LeftAcc =< Mid -> LeftValue = element(LeftAcc, Tuple), merge(Tuple, Left, Mid, Right, LeftAcc + 1, MidAcc, [LeftValue | TempAcc]); merge(Tuple, Left, Mid, Right, LeftAcc, MidAcc, TempAcc) when MidAcc =< Right -> RightValue = element(MidAcc, Tuple), merge(Tuple, Left, Mid, Right, LeftAcc, MidAcc + 1, [RightValue | TempAcc]); merge(Tuple, Left, _Mid, _Right, _LeftAcc, _MidAcc, TempAcc) -> copy_merge(lists:reverse(TempAcc), Left, Tuple). %% 将临时列表中的元素复制回tuple copy_merge([H | TempAcc], Left, Tuple) -> NewTuple = erlang:setelement(Left, Tuple, H), copy_merge(TempAcc, Left + 1, NewTuple); copy_merge([], _Left, Tuple) -> Tuple.


