分治法设计思想:
1、将原问题分解为几个规模较小但类似于原问题的子问题,递归地求解这些子问题,然后再合并这些子问题的解来建立原问题的解;
2、解决问题所需的计算时间都与其规模有关,问题的规模越小,越容易求解,所需的计算时间也越少。分治法就是将一个难以解决的大规模的问题,拆分成规模小且所需计算时间少的相同问题,分别解决;
3、许多有用的算法在结构上是递归的:为了解决一个给定的问题,算法一次或多次递归的调用其自身以解决紧密相关的若干子问题(如:归并排序、快速排序、二分搜索等)。这些算法典型的采用了分治法的设计思想;
分治法步骤:
1、分解原问题为若干子问题,这些子问题是原问题的规模较小的实例;
2、解决这些子问题,递归地求解各子问题。如果子问题的规模足够小,则直接求解;
3、合并这些子问题的解成原问题的解(如果子问题是不独立的,紧密则会导致重复求解相同的子问题,会降低分治法效率,一般会采用动态规划);
什么时候可以使用分治法:
1、问题可以拆分为若干个规模较小的相同问题,且拆分成小规模后可以很简单的解决;
2、利用拆分成子问题的解能够合并为原问题的解;
3、分解出的各个子问题是相互独立的,
分析分治算法:
当一个算法包含对其自身的递归调用时,我们往往可以用递归方程或递归式来描述其运行时间;
如果一个问题的规模为n,假设将问题分解成a个子问题,每个子问题的规模是原问题的1/b。由此可知每个子问题的求解时间为T(n/b),如果分解成子问题需要时间D(n),合并子问题的解需要时间C(n),则得到递归式:T(n) = aT(n/b) + D(n) + C(n);
求解递归式一般有三个方法:
1、代入法:猜测一个界,然后使用数学归纳法证明这个界是正确的,分三个步骤:
(1)凭感觉猜,不用关系系数和常数,猜测可能的形式;
(2)通过数学归纳法验证第一步才出来的form是否满足条件;
(3)确定系数和常数;
2、递归树法:将递归式转换成一棵树,其结点表示不同层次的递归调用产生的代价,然后采用边界和技术求解。如下图归并算法的递归树(a=2原问题可以分解成2个子问题,子问题是原问题的1/2规模, D(n)因为只比较子数组的中间位置,所以是常数):
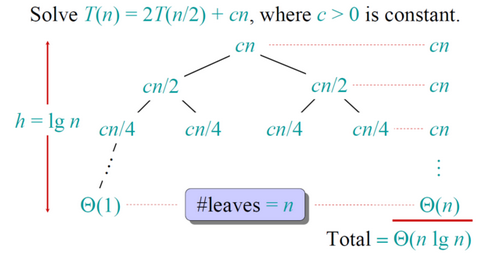
3、主方法依赖定理:设a ≥ 1 和 b>1为常数,设f(n)为一函数,T(n)由递归式T(n) = aT(n/b) + f(n)对非负整数定义,则可能有如下渐近界:
(1)若对于某常数ε>0,有f(n) = O(n^(log_b(a)-ε)),则T(n) = Ө( n^(log_b(a)) );
(2)若f(n)=Ө(n^(log_b(a))),则T(n) = Ө(n^(log_b(a)) * lgn);
(3)若对某常数ε>0,有f(n)=Ω(n^(log_b(a) + ε)),且对常数c<1与足够大的n,有a*f(n/b) ≤ c*f(n),则T(n) = Ө(f(n));
以上三种情况需要记忆,能够解决一般情况下的递归式求解。




