OO第三单元作业总结
一、实现规格所采取的设计策略
前两次作业由于功能简单,我自己并没有自己设计新的类来凸显层次化,基本上时按照官方给的接口来设计类实现。
但是第三次作业,功能越来越多,不进行层次化设计会导致某个类过于复杂(Network),因此第三次作业,我将针对同一类对象的操作和该类对象单独封装成一类(box类),而Network仅仅充当调用方和具体实现方之间的”接口“类。Network只负责调用box中的方法并组合向上提供功能。
二、整理基于JML规格来设计测试的方法和策略
-
策略
理清方法规格的控制流,保证每一个控制流都能测试到。针对每一个控制分支,测试其是否正确执行。测试基于对方法规格的理解,因此保证严格按照方法规格描述得到正确结果。
第三次作业就是因为这里踩坑,对于数值的计算,务必严格严格严格按照方法规格执行。 -
方法
针对每一个控制分支的条件设置初始条件,使得每一个分支可以被测试到。每一个分支执行的结果打印到屏幕上进行检查。分支内方法正确性通过输入边缘极端数据和普通数据验证打印出的结果。测试的正确结果是完全按照方法规格定义计算得到的,尤其对数值的计算,切忌将规格转换成自然语言理解并检验结果,而是严格执行方法规格验证结果。最后找到一个大佬借用自动测评机进行对拍(不是)。
三、总结分析容器选择和使用的经验
-
对于保证数据的新旧顺序的需求,选择ArrayList或数组。比如本次作业的最近收到消息所用容器,朋友列表。
-
对于查找数据存在性的需求,选择HashSet,比如本次作业的dijikstra中的点集,人所加入的群集合;
-
对于需要访问容器中某一数据的,选择HashMap,选择适当属性作为key,数据作为value。本次作业多次用到Map:并查集的父亲信息,人、消息、群的存储,朋友value的存储,到固定点最短路径长度的存储。
-
对于把数据按照某一标准排序存储的需求,选择PriorityQueue。优先队列是封装好的实现堆排序的容器,性能不错,比如查找当前的和源点距离最小的点时用的工具队列。
四、性能问题和优化时遇到的bug
本次作业涉及到的性能问题有三处:第一处查找两点是否可达(iscircle)和连通分支数(queryBlockSum),第二处是查找群中所有相互认识的<人,人>,并将所有对的value求和,第三处求两点之间的最短路径(sendIndirectMessage)。
-
并查集
第一处查找是否可达若通过循环递归,即递归遍历所有朋友直到找到目标人或所有人都已进行查找,开销大,性能差。统计最小连通图的个数如通过遍历方法在所有点都孤立的情况下有O(n*n)的复杂度。
因此可通过并查集策略提升性能
,但我由于对算法理解不准确,导致强测爆点。并查集的实现是维护每一个人的所在组的组长。在加入关系后,修改两个人分别所在组的组长的指向,然后通过对所有点递归维护所有人的所在组的组长确保其指向最终的组长。决定谁是组长按照统一的规则(来的先后,id大小等),所有人初始组长是自己。如此,两个人可达等价于两个人在一个组。最小连通图的个数就是组数,即有多少人所在组的组长是自己。并查集的维护开销在于维护所有人的所在组的组长,最差的复杂度是O(n*n),很极端的单链结构。其实这里还可以进一步优化,在确立组长时可以依据树的高度,让高度低的组的组长认高度高的组的组长为自己的组长,从而降低整体树的高度,降低查找最终组长的时间,降低维护成本。另外可以在查找最终组长的递归过程中,在每层返回时,修改当前结点的组长为最终组长,即一次可以维护一条链上所有点的最终组长。实现并查集后统计最小连通图个数的复杂度为O(n),只用遍历一遍组长数组并对组长是自己的点求和。因此并查集显著提升了性能。
-
维护局部变量
第二处查找所有相互认识的<人,人>并对他们的value求和若通过二重循环遍历,复杂度是O(n*n)。
因此可通过维护group的valuesum属性提升性能:某人加群(addToGroup)时遍历群中所有人,若认识该人,则valuesum加上两倍的value;某人退群时遍历群中所有人,若认识该人,则valuesum减去两倍的value。这里我踩了第一个坑,没有在加关系时维护valuesum,因为有人是先加群再加的好友。解决方式是在加群时人记录自己所在群(inGroup),并在加关系时遍历两人都在的群,维护群的valuesum。紧接着还有第二个坑,退群时,忘记修改人的inGroup属性,导致bug。
维护valuesum在加群时复杂度为O(n),n是群中人数;加关系时复杂度是O(m),m不超过群数;退群时复杂度为O(n),n为群中人数;维护inGroup复杂度为O(1),因此显著降低了开销,提升了性能。
-
堆优化
第三处通过dijkstra求最短路径。这里我踩了第一个坑,对dijkstra理解错误。改正后性能不够,采用堆优化提升性能
,这次总算没有bug了。朴素的dijkstra算法复杂度是O(n*n),n为人的数量,性能开销主要在于每次查找当前和源点距离最近的点。因此可通过把每次维护后的点到原点的距离加入优先队列中,利用堆排序对其排序,距离最近的点就是队首的点。
堆排序的复杂度是O(logn),总体复杂度下降,性能提升。
五、架构设计与图模型
-
架构设计
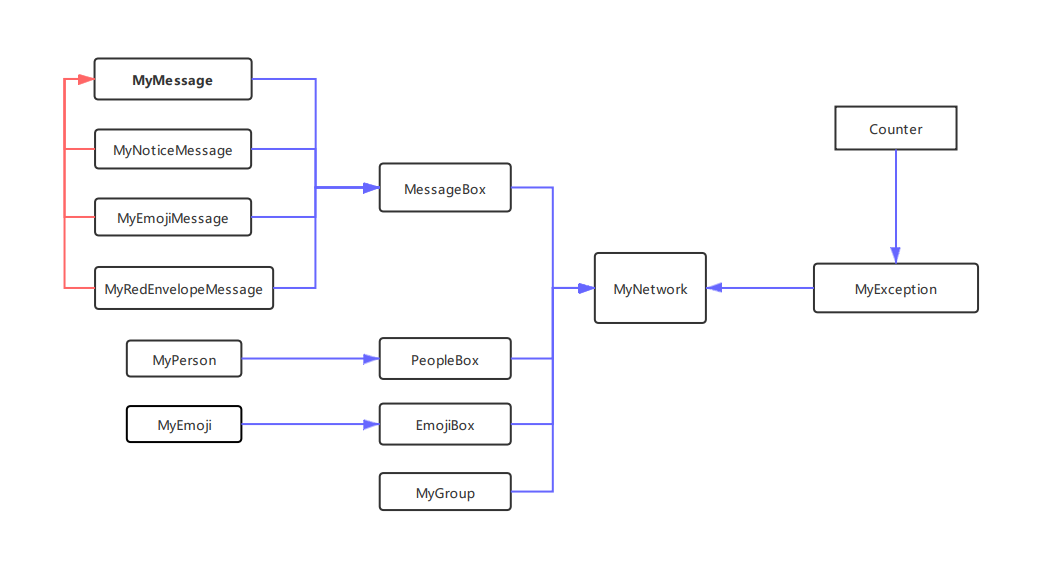
接着第一大点的设计策略,我将关系紧密的数据结构和方法单独成类,因此新增了peoplebox类、messagebox类、emojibox类。
上面说的并查集策略、dijkstra算法,money的操作,inGroup的维护等方法封装在peoplebox中,关于消息的添加、删除、查找和emojiMessage的删除等方法封装在messagebox中,关于emoji的添加、删除、增长热度等方法封装在enojibox中。
Network组合了peoplebox、messagebox、emojibox、groups。Network就是图,peoplebox相当于距离矩阵,每一个person记录了矩阵的对应行向量。
![]()
-
架构简析
像上图所示,在network中的方法通过调用和组合box中方法来实现。这样增大了调用方法的粒度,但同时加大了组合方法的难度,有利有弊。之所以组合方法,是因为部分方法需要message、people、emoji、group共同参与。
六、反思与收获
-
使用一些策略和算法时,一定要理解透彻他们。
-
书写方法时,一定要严格按照方法规格书写,特别是计算相关语句,切忌想当然修改计算方式。
-
对涉及到算法的方法和涉及到多个方法调用的较复杂方法,一定要多次检查、测试。
-



 浙公网安备 33010602011771号
浙公网安备 33010602011771号