2.1 点估计
点估计:对于给定的总体和样本,如果用某个统计量的值估计总体的某个未知参数,这种估计方法称为点估计,该统计量称为点估计量。例如用样本均值 估计总体均值,用样本方差
估计总体均值,用样本方差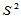 估计总体方差,都属于点估计。
估计总体方差,都属于点估计。
常用的求点估计量的方法有:矩估计法、最大似然估计法,是考研究生要求掌握的方法,常用教材都有详细叙述。
对于同一个未知参数,常有多种估计方法,如何选择?这涉及到估计量的评价标准。常从以下三个不同角度考察。
2.1.1 无偏性
定义1.5 设总体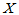 含有未知参数
含有未知参数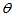 ,
,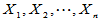 为来自总体的简单随机样本,又设
为来自总体的简单随机样本,又设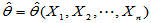 为
为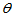 的一个估计量。若在给定范围内无论
的一个估计量。若在给定范围内无论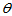 如何取值,总有
如何取值,总有 ,则称
,则称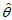 为
为 的一个无偏估计量;若
的一个无偏估计量;若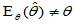 ,则称
,则称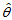 为
为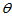 的一个有偏估计量。
的一个有偏估计量。
注意无偏估计的含义是:由于样本的随机性,估计值有时候偏大,有时候偏小,多次估计的平均值才能靠近真实的未知参数值。
无论无偏估计还是有偏估计,可以统一使用"均方误差"MSE评价:
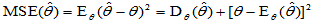 (2-1)
(2-1)
对于无偏估计,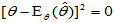 ,但
,但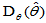 可能很大,果真如此,它就不是一个好的估计量。反之,对于有偏估计,虽然
可能很大,果真如此,它就不是一个好的估计量。反之,对于有偏估计,虽然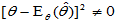 ,但如果与
,但如果与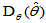 相加之后
相加之后 仍然较小,则它就是一个较好的估计量。
仍然较小,则它就是一个较好的估计量。
例2.1 设总体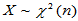 ,
,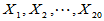 为来自总体的简单随机样本,欲估计总体均值
为来自总体的简单随机样本,欲估计总体均值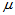 (注意
(注意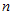 未知),比较以下三个点估计量的好坏:
未知),比较以下三个点估计量的好坏:
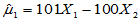 ,
,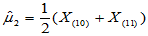 ,
,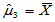
解 本例题给出了利用MSE评价点估计量的随机模拟方法。由于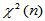 的总体均值为
的总体均值为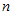 ,因此我们可以先取定一个固定值,例如
,因此我们可以先取定一个固定值,例如 ,然后在这个参数已知且固定的总体中抽取容量为20的样本,分别用样本值依照三种方法分别计算估计值(注意谁也别偷看底牌
,然后在这个参数已知且固定的总体中抽取容量为20的样本,分别用样本值依照三种方法分别计算估计值(注意谁也别偷看底牌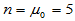 ),看看哪种方法误差大,哪种方法误差小。一次估计的比较一般不能说明问题,正如低手射击也可能命中10环,高手射击也可能命中9环。如果连续射击1万次,比较总环数(或平均环数),多者一定是高手。同理,如果抽取容量为20的样本
),看看哪种方法误差大,哪种方法误差小。一次估计的比较一般不能说明问题,正如低手射击也可能命中10环,高手射击也可能命中9环。如果连续射击1万次,比较总环数(或平均环数),多者一定是高手。同理,如果抽取容量为20的样本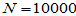 次,分别计算
次,分别计算
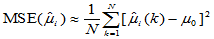
小者为好。
N=10000; m=5; n=20;
mse1=0; mse2=0; mse3=0;
for k=1:N
x=chi2rnd(m,1,n);
m1=101*x(1)-100*x(2);
m2=median(x);
m3=mean(x);
mes1=mse1+(m1-m)^2;
mes2=mse2+(m2-m)^2;
mes3=mse3+(m3-m)^2;
end
mse1=mes1/N
mse2=mes2/N
mse3=mes3/N
以上程序保存为ex21.m,命令窗口中键入ex21,运算结果为
mse1 =
58.1581
mse2 =
7.8351e-005
mse3 =
9.4469e-006
可见第一个虽为无偏估计量,但MSE极大,表现很差。第二个虽为有偏估计,但表现与第三个相差不多,也是较好的估计量。另外,重复运行ex21,每次的结果是不同的,但优劣表现几乎是一致的。
例2.2 设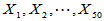 为来自
为来自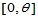 上服从均匀分布的总体的简单随机样本,容易得到未知参数的矩估计量
上服从均匀分布的总体的简单随机样本,容易得到未知参数的矩估计量 ,最大似然估计量
,最大似然估计量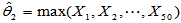 ,试用随机模拟的方法比较两者的优劣。
,试用随机模拟的方法比较两者的优劣。
解 不妨设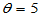 ,以下程序给出了两者的评价。
,以下程序给出了两者的评价。
s=5;
N=10000;
mse1=0; mse2=0;
for k=1:N
x=5.*rand(1,50);
s1=2*mean(x);
s2=max(x);
mse1=mse1+(s1-s)^2;
mse2=mse2+(s2-s)^2;
end
mse1=mse1/N; mse2=mse2/N;
[mse1,mse2]
参考运行结果: 0.1655 0.0186
本例中,最大似然估计精度较高。注意矩法估计量是无偏估计,本例中最大似然估计量显然是有偏估计,且一定是偏小的。
2.1.2 有效性
对于无偏估计,在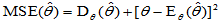 中第二项为零,故比较两个无偏估计量,只需比较各自的方差即可。称方差小的无偏估计量为有效的,当然指的是两个无偏估计相对而言。
中第二项为零,故比较两个无偏估计量,只需比较各自的方差即可。称方差小的无偏估计量为有效的,当然指的是两个无偏估计相对而言。
2.1.3 相合性
设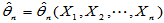 为总体未知参数
为总体未知参数 的估计量,如果对于任意给定的
的估计量,如果对于任意给定的 ,总有
,总有
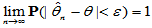 (2-2)
(2-2)
则称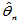 为
为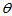 的相合估计量。又若
的相合估计量。又若
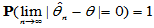 (2-3)
(2-3)
则称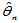 为
为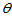 的强相合估计量。
的强相合估计量。
相合估计的含义是:样本容量越大,估计值越精确。
2.2 区间估计
所谓区间估计,就是用两个估计量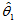 与
与 估计未知参数
估计未知参数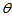 ,使得随机区间
,使得随机区间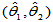 能够包含未知参数的概率为指定的
能够包含未知参数的概率为指定的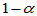 。即:
。即:
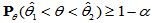
称满足上述条件的区间 为
为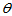 的置信区间,称
的置信区间,称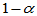 为置信水平。
为置信水平。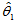 称为置信下限,
称为置信下限,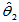 称为置信上限。
称为置信上限。
2.2.1 单正态总体均值的置信区间
(1)方差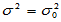 已知情形
已知情形
查表求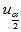 满足:对于
满足:对于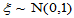 ,
,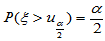 。
。
对于总体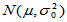 中的样本
中的样本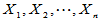 ,
,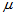 的置信区间为:
的置信区间为:
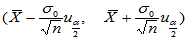 (2-4)
(2-4)
其中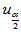 可以用norminv(1-a /2)计算。
可以用norminv(1-a /2)计算。
例2.3 设
1.1, 2.2, 3,3, 4.4, 5.5
为来自正态总体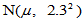 的简单随机样本,求
的简单随机样本,求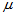 的置信水平为95%的置信区间。
的置信水平为95%的置信区间。
解 以下用Matlab命令计算:
x=[1.1,2.2,3.3,4.4,5.5];
n=length(x);
m=mean(x);
c=2.3/sqrt(n);
d=c*norminv(0.975);
a=m-d; b=m+d;
[a,b]
计算结果为 1.2840 5.3160
(2)方差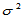 未知情形
未知情形
对于总体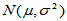 中的样本
中的样本 ,
, 的置信区间为:
的置信区间为:
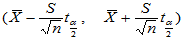 (2-4)
(2-4)
其中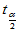 为自由度
为自由度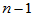 的
的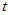 分布临界值。
分布临界值。
数据同上,继续利用Matlab计算
S=std(x); dd=S*tinv(0.975,4)/sqrt(n);
aa=m-dd; bb=m+dd; [aa,bb]
结果为 1.1404 5.4596
2.2.2 单正态总体方差的置信区间
由于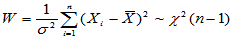 ,查表求临界值
,查表求临界值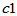 与
与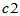 ,使得
,使得

则 的置信区间为
的置信区间为
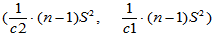 (2-5)
(2-5)
其中查表可用chi2inv进行。数据同上,以下求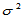 的置信区间。
的置信区间。
c1=chi2inv(0.025,4);
c2=chi2inv(0.975,4);
T=(n-1)*var(x);
aaa=T/c2; bbb=T/c1;
[aaa,bbb]
计算结果为 1.0859 24.9784
2.2.3 两正态总体均值差的置信区间
(1)方差已知情形
设 ,
, ,两样本独立,此时
,两样本独立,此时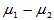 的置信区间为
的置信区间为
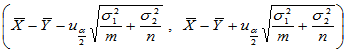 (2-6)
(2-6)
这里我们已经知道 可用norminv(0.975)求得,Matlab计算很容易。
可用norminv(0.975)求得,Matlab计算很容易。
(2)方差未知但相等: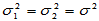
此时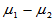 的置信区间为
的置信区间为
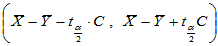 (2-7)
(2-7)
其中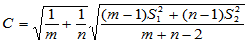 ,而
,而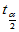 依照自由度
依照自由度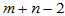 计算。
计算。
2.2.4 两正态总体方差比的置信区间
此时,查自由度为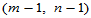 的
的 分布临界值表,使得
分布临界值表,使得
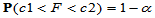
则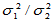 的置信区间为:
的置信区间为:
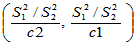 (2-7)
(2-7)
例2.4 设两台车床加工同一零件,各加工8件,长度的误差为:
A:-0.12 -0.80 -0.05 -0.04 -0.01 0.05 0.07 0.21
B:-1.50 -0.80 -0.40 -0.10 0.20 0.61 0.82 1.24
求方差比的置信区间。
解 用Matlab计算如下:
x=[-0.12,-0.80,-0.05,-0.04,-0.01,0.05,0.07,0.21];
y=[-1.50,-0.80,-0.40,-0.10,0.20,0.61, 0.82,1.24];
v1=var(x); v2=var(y);
c1=finv(0.025,7,7); c2=finv(0.975,7,7);
a=(v1/v2)/c2; b=(v1/v2)/c1; [a,b]
计算结果为: 0.0229 0.5720
方差比小于1的概率至少达到了95%,说明车床A的精度明显高。




