第十二章 B样条曲面
B样条曲面在CAD/CAM中具有非常重要的地位,它可由B样条曲线通过直积推广而得,正如由Bézier曲线经由直积推广而得Bézier曲面一样。本章主要讨论B样条曲面的性质及其相关的配套技术。
12.1 B样条曲面的定义及性质
给定三维空间 个点
个点 ,参数
,参数 和
和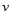 的节点矢量
的节点矢量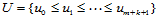 、
、 ,参数曲面:
,参数曲面:
 (12.1.1)
(12.1.1)
称为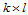 次B样条曲面。式中
次B样条曲面。式中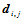 称为曲面的控制顶点或de Boor点,逐次用线段连接点列
称为曲面的控制顶点或de Boor点,逐次用线段连接点列 中相邻两点组成的空间网格叫做曲面的控制网格或de Boor网格,
中相邻两点组成的空间网格叫做曲面的控制网格或de Boor网格, 分别是由节点矢量
分别是由节点矢量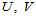 定义的规范B样条基函数,次数分别为
定义的规范B样条基函数,次数分别为 和
和 。
。
由式(12.1.1)可以看出,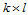 次B样条曲面是由
次B样条曲面是由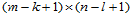 片
片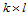 次参数多项式曲面组合而成的多项式样条曲面。其性质可由B样条曲线的性质推广而得。
次参数多项式曲面组合而成的多项式样条曲面。其性质可由B样条曲线的性质推广而得。
1. 局部性。 次B样条曲面上参数为
次B样条曲面上参数为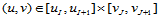 的点
的点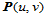 至多与
至多与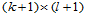 个控制顶点
个控制顶点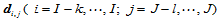 有关,与其他控制顶点无关。移动控制顶点
有关,与其他控制顶点无关。移动控制顶点 至多影响到定义在区域
至多影响到定义在区域 上的那一部分曲面形状,对曲面的其余部分不产生影响。
上的那一部分曲面形状,对曲面的其余部分不产生影响。
2. 参数连性。B样条曲面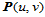 的每一片
的每一片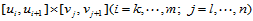 在其内部
在其内部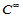 连续,而在节点
连续,而在节点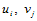 处则是
处则是 连续,其中
连续,其中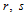 分别是节点
分别是节点 的重数。
的重数。
3. 凸包性。B样条曲面的每一片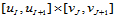 都位于定义该片曲面的控制顶点
都位于定义该片曲面的控制顶点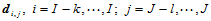 ,的凸包之中,整个B样条曲面位于定义各片曲面的控制顶点的凸包的并集之中。这样以来,B样条曲面的凸包区域就比同一组顶点定义的Bézier曲面的凸包区域要小,至多相同。
,的凸包之中,整个B样条曲面位于定义各片曲面的控制顶点的凸包的并集之中。这样以来,B样条曲面的凸包区域就比同一组顶点定义的Bézier曲面的凸包区域要小,至多相同。
由凸包性质可以导出以下结果:
- 若控制顶点
 重合时,由这
重合时,由这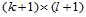 个控制顶点定义的
个控制顶点定义的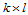 次B样条曲面片便退化为这个重合点;
次B样条曲面片便退化为这个重合点;
- 若上述的
 个控制顶点共面,那么所定义的曲面片便是平面片。
个控制顶点共面,那么所定义的曲面片便是平面片。
4. 磨光性质等。同一组控制顶点定义的B样条曲面,随着次数的升高越来越光滑。
5. 仿射不变性。B样条曲面在仿射变换下不便。
6. 对Bézier曲面的包含性。若
 ,且参数节点矢量
,且参数节点矢量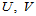 选择如下:
选择如下:

则由此确定的B样条曲面就是
 次Bézier曲面。
次Bézier曲面。
7. 等参数线。固定
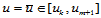 ,那么曲线
,那么曲线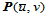 是一条
是一条 次B样条曲线,其控制顶点为
次B样条曲线,其控制顶点为
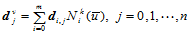
同理,固定
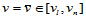 ,其参数曲线
,其参数曲线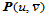 为一条
为一条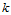 次B样条曲线,相应的控制顶点为
次B样条曲线,相应的控制顶点为
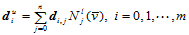
然而,与Bézier曲面一样,变差缩减性对B样条曲面将不再成立。
12.2 B样条曲面的分类
按照参数节点矢量的不同,可将B样条曲面划分为以下四种类型:
- 均匀B样条曲面(Uniform B-spline Surfaces)。节点矢量
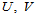 满足条件:
满足条件:
 ,
, (12.2.1)
(12.2.1)
 ,
,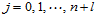 (12.2.2)
(12.2.2)
- 准均匀B样条曲线(Quasi-Uniform B-spline Surfaces)。节点矢量
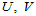 满足条件:
满足条件:
 (12.2.3)
(12.2.3)
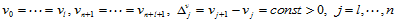 (12.2.4)
(12.2.4)
- 分片Bézier曲面(Piecewise Bézier Surfaces)。节点矢量
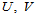 满足的条件是:
满足的条件是:
 (12.2.5)
(12.2.5)
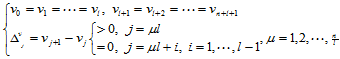 (12.2.6)
(12.2.6)
选择该类型B样条曲面有一个限制:
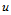 向控制顶点个数减1必须等于次数
向控制顶点个数减1必须等于次数 的整数倍,即
的整数倍,即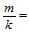 正整数。这样的节点矢量定义了分段Bernstein基函数。同理,
正整数。这样的节点矢量定义了分段Bernstein基函数。同理,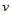 向控制顶点个数减1也必须等于次数
向控制顶点个数减1也必须等于次数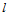 的整数倍。
的整数倍。
- 均匀B样条曲面(Uniform B-spline Surfaces)。节点矢量
- 非均匀B样条曲面(General Non-Uniform B-spline Surfaces)。对于这种类型的B样条曲面,只要节点矢量满足以下条件即可:
- 节点序列非递减;
- 两端节点的重数
 次数+1,内节点的重数
次数+1,内节点的重数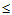 次数。
次数。
12.3 双三次均匀B样条曲面
双三次均匀B样条曲面是最为重要的一种曲面格式。给定控制顶点

 ,其每一片曲面可表示如下:
,其每一片曲面可表示如下:
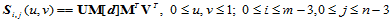 (12.3.1)
(12.3.1)
式中,
 。
。
 ,
,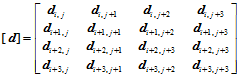
它是一双三次多项式曲面。这样以来,对于同一张双三次参数曲面而言,我们有三种表示形式:Bézier形式、Hermite形式和B样条形式。因此,三种表示形式之间可以相互转换。
12.4 de Boor-Cox算法
类似于B样条曲线上点的计算,B样条曲面上的点的计算亦可由一系列线性插值来完成,对应的算法称之为de Boor-Cox算法。
对于给定的
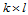 次B样条曲面
次B样条曲面

其参数为
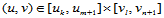 的点
的点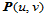 可计算如下。设
可计算如下。设 ,
,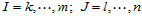 :
:
算法1.
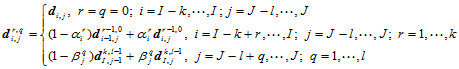 (12.4.1)
(12.4.1)
其中,
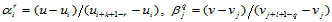 。
。
算法2.
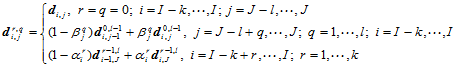 (12.4.2)
(12.4.2)
当按算法1进行时,先以参数值
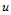 对控制网格沿
对控制网格沿 向的
向的 个多边形执行曲线的de Boor-Cox算法,
个多边形执行曲线的de Boor-Cox算法,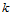 级递推后,得到沿
级递推后,得到沿 向的由
向的由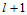 个顶点
个顶点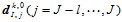 构成的中间多边形。再以参数
构成的中间多边形。再以参数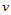 对其执行曲线的de Boor-Cox算法,
对其执行曲线的de Boor-Cox算法,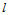 级递推后,得到曲面上对应的点
级递推后,得到曲面上对应的点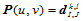 。算法2的执行次序恰好与算法1相反。
。算法2的执行次序恰好与算法1相反。
特别,当
 时,上述两个算法可合并成一双参数线性插值。
时,上述两个算法可合并成一双参数线性插值。
算法3.
 (12.4.3)
(12.4.3)
上述算法中的任一种所得结果完全相同,其时间复杂度亦完全一样。
12.5 B样条曲面的偏导矢
B样条曲面的偏导矢的计算也可由B样条曲线导矢计算公式直接推广而得。
- 单向导矢:
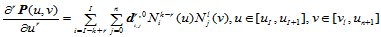 (12.5.1)
(12.5.1)
其中
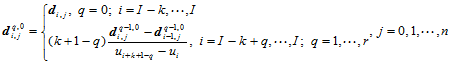 (12.5.2)
(12.5.2)
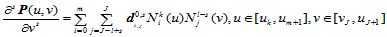 (12.5.3)
(12.5.3)
这里
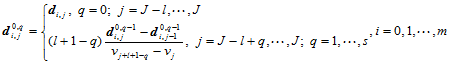 (12.5.4)
(12.5.4)
- 混合偏导矢
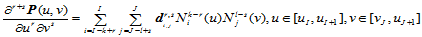 (12.5.5)
(12.5.5)
控制顶点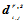 可按下述递归公式求得:
可按下述递归公式求得:
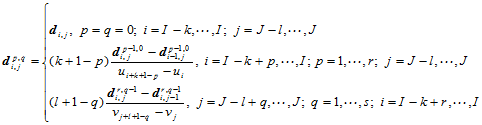 (12.5.6)
(12.5.6)
12.6 B样条曲面的节点插入
节点插入是B样条方法中最为重要的技术之一,它既具有重要的理论意义,又杂曲线曲面设计中有着广泛的用途。
设给定一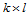 次B样条曲面:
次B样条曲面:
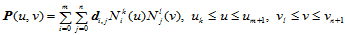 (12.6.1)
(12.6.1)
其中,定义B样条基函数的节点矢量分别为
 ,
,
那么,对于B样条曲面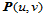 而言,其节点的插入与B样条曲线的节点插入相似,区别仅在于这里既可以在
而言,其节点的插入与B样条曲线的节点插入相似,区别仅在于这里既可以在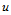 向插入节点,也可以在
向插入节点,也可以在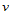 向插入节点,还可以在两个参数方向同时插入节点。
向插入节点,还可以在两个参数方向同时插入节点。
12.6.1 单向节点插入
给定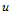 向一参数
向一参数 ,将其作为一个节点插入到节点矢量
,将其作为一个节点插入到节点矢量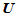 中,于是得到一新的节点矢量
中,于是得到一新的节点矢量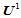 :
:
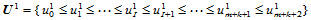
其中:
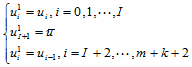 (12.6.2)
(12.6.2)
节点矢量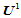 可定义
可定义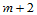 个
个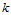 次B样条基函数
次B样条基函数 ,原来的
,原来的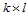 次B样条曲面就可用这组新的B样条基函数和未知的新控制顶点
次B样条曲面就可用这组新的B样条基函数和未知的新控制顶点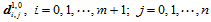 ,表示出:
,表示出:
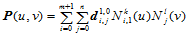
此时,控制顶点增加了一排,而曲面的形状及连续性保持不变。未知控制顶点 可计算如下:
可计算如下:
 (12.6.3)
(12.6.3)
其中
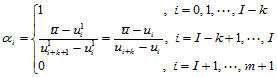 (12.6.4)
(12.6.4)
插入一个节点后,控制顶点增加了一排,共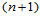 个。该算法实质上就是de Boor-Cox算法求
个。该算法实质上就是de Boor-Cox算法求 次B样条曲线上一点
次B样条曲线上一点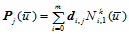 ,
,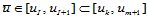 时,其第一级递推的中间点。它仅涉及到
时,其第一级递推的中间点。它仅涉及到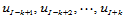 这
这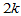 个节点,
个节点,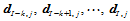 这
这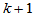 个控制顶点。用生成的中间顶点
个控制顶点。用生成的中间顶点 取代老顶点
取代老顶点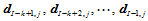 而保持其余顶点不变。该算法可图解如下:
而保持其余顶点不变。该算法可图解如下:

图12.1 节点插入
同理,若给定 向一参数
向一参数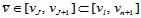 ,将其作为一个节点插入到节点矢量
,将其作为一个节点插入到节点矢量 中,于是得到一新的节点矢量
中,于是得到一新的节点矢量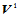 :
:
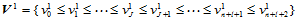
其中:
 (12.6.5)
(12.6.5)
曲面 亦可由节点矢量
亦可由节点矢量 定义的新B样条基函数
定义的新B样条基函数 和未知的新控制顶点
和未知的新控制顶点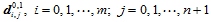 表示如下:
表示如下:

此时,控制顶点也增加了一排,而曲面的形状及连续性保持不变。未知控制顶点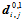 的计算方法如下:
的计算方法如下:
 (12.6.6)
(12.6.6)
其中
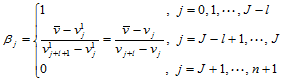 (12.6.7)
(12.6.7)
12.6.2 两个方向同时插入节点
给定两个方向的参数 、
、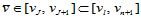 ,将其分别插入到各自的节点矢量中,则曲面
,将其分别插入到各自的节点矢量中,则曲面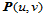 可由未知控制顶点
可由未知控制顶点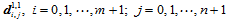 和新的基函数表示如下:
和新的基函数表示如下:

未知控制顶点 的计算公式是:
的计算公式是:
 (12.6.8)
(12.6.8)
这里, 的定义同上。
的定义同上。
当然,也可以象B样条曲线那样,我们可以将一个节点重复插入 次。
次。
12.6.3 顶点插入
插入节点尽管是非常有效的交互设计工具,但节点不具有清晰的几何意义。为此,我们采用一种与插入节点不同的方法,即指定一个确定的点作为新的控制顶点,来反求出需要插入的节点。这就是B样条方法的插入顶点技术。
给定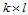 次B样条曲面:
次B样条曲面:

假设在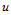 向插入一新的控制顶点
向插入一新的控制顶点 ,它位于控制网格的边
,它位于控制网格的边 上。于是,
上。于是,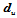 可表示为:
可表示为:
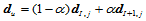
由此, 。那么,令:
。那么,令:
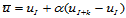 (12.6.9)
(12.6.9)
则参数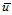 即为要插入的节点。
即为要插入的节点。
类似地,在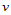 向插入一新的控制顶点
向插入一新的控制顶点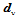 ,它位于控制网格的边
,它位于控制网格的边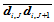 上。于是有:
上。于是有:
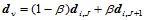
则, 。此时,
。此时,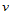 向要插入的节点是:
向要插入的节点是:
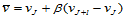 (12.6.10)
(12.6.10)
若仅在一个参数方向对原始控制网格插入一个新的控制顶点,反插节点的结果将使该参数方向每排顶点都增加一个。在 向和
向和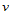 向分别插入新的控制顶点
向分别插入新的控制顶点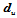 与
与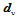 的结果使每个参数方向上每排顶点都增加一个。在这个过程中,某些老顶点被新顶点所替代。
的结果使每个参数方向上每排顶点都增加一个。在这个过程中,某些老顶点被新顶点所替代。
若要插入的新控制顶点 位于控制网格的顶点
位于控制网格的顶点 所确定的双一次曲面上,则存在
所确定的双一次曲面上,则存在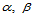 ,使得:
,使得:
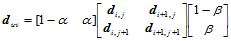 (12.6.11)
(12.6.11)
此时,在在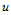 向和
向和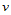 向分别要插入的节点是:
向分别要插入的节点是:
 (12.6.12)
(12.6.12)
 (12.6.13)
(12.6.13)




