§6.1 数理统计的基本概念
一.数理统计研究的对象
例:有一批灯泡,要从使用寿命这个数量指标来看其质量,设寿命用X表示。
(1)若规定寿命低于1000小时的产品为次品。此问题是求P(X£1000)=F(10000),求F(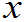 )?
)?
(2)从平均寿命、使用时数长短差异来看其质量,即求E(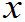 )?、D(
)?、D(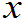 )?。
)?。
要解决二个问题
1.试验设计抽样方法。
2.数据处理或统计推断。
方法具有"从局部推断总体"的特点。
二.总体(母体)和个体
1.所研究对象的全体称为总体,把组成总体的每一个对象成员(基本单元)称为个体。
说明:
- 对总体我们关心的是研究对象的某一项或某几项数量指标(或属性指标)以及他们在整体中的分布。所以总体是个体的数量指标的全体。
(2)为研究方便将总体与一个R.V X对应(等同)。
- 总体中不同的数量指标的全体,即是R.V.X的全部取值。
- R.V X的分布即是总体的分布情况。
例:一批产品是100个灯泡,经测试其寿命是:
1000小时 1100小时 1200小时
20个 30个 50个
X 1000 1100 1200
P 20/100 30/100 50/100
(设X表示灯泡的寿命)可知R.V.X的分布律,
就是总体寿命的分布,反之亦然。
常称总体X,若R.VX~F(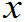 ),有时也用F(
),有时也用F(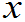 )表示一个总体。
)表示一个总体。
(3)我们对每一个研究对象可能要观测两个或多个数量指标,则可用多维随机向量(X,Y,Z, …)去描述总体。
2.总体的分类
有限总体
无限总体
三.简单随机样本.
1.定义6.1 :从总体中抽得的一部分个体组成的集合称为子样(样本),取得的个体叫样品,样本中样品的个数称为样本容量(也叫样本量)。每个样品的测试值叫观察值。
取得子样的过程叫抽样。
样本的双重含义:
(1)随机性:
用( X
X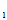 ,X
,X ,……X
,……X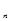 ) n维随机向量表示。
) n维随机向量表示。
X 表示第i个被抽到的个体,是随机变量。(i=1,2,…n)
表示第i个被抽到的个体,是随机变量。(i=1,2,…n)
(2)确定性:
(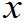
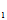 ,
,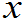
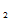 ,……
,……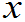
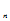 )表示n个实数,即是每个样品X
)表示n个实数,即是每个样品X 观测值
观测值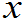
 (i=1,2,…n)。
(i=1,2,…n)。
2.定义6.2:
设总体为X,若X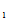 ,X
,X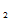 ……X
……X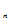 相互独立且与X同分布,则称(X
相互独立且与X同分布,则称(X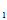 ,X
,X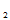 …X
…X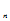 )为来自总体X的容量为n的简单随机样本(简称样本)。
)为来自总体X的容量为n的简单随机样本(简称样本)。
3.已知总体的分布写出子样的分布
(1)已知总体X~F(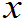 ),则样品X
),则样品X ~
~ F(
F(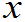
 ) i=1,2…n样本(X
) i=1,2…n样本(X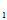 ,X
,X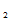 …X
…X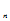 )的联合分布为:
)的联合分布为:
F(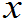
 ,
,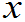
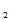 …
…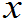
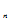 )=P(X
)=P(X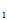
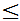
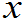
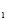 ,X
,X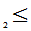
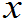
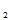 …X
…X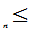
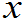
 )
)
=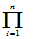 P(X
P(X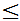
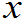
 )
)
=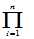 F(
F(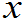
 )
)
若总体X~f(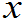 ),样品X
),样品X ~f(
~f(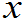
 ) i=1,2……n
) i=1,2……n
样本(X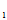 ,X
,X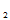 ……X
……X )的联合密度是
:
)的联合密度是
:
f(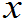
 ,
,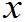
 ……
……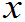
 )=
)=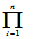 f(
f(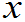
 )
)
例:总体X~N(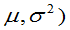 ,写出该总体样本(X
,写出该总体样本(X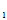 ,X
,X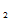 …X
…X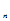 )的
联合密度。
)的
联合密度。
(2)若总体X是离散型随机变量,一般给出分布律:
P(X=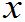 k) = pk. k=1,2……
k) = pk. k=1,2……
要写出概率函数f(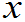 )即f(
)即f(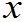 )=P(X=
)=P(X=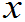 k)=
k)=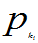
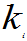 =1,2…..,
=1,2….., 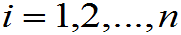
例: 总体X~p(l)写出该总体样本(X1,X2,…Xn)的联合概率函数
例:总体X~B(1,p), 0<p<1写出其样本
(X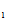 ,X
,X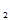 ,……X
,……X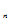 )的联合概率函数。
)的联合概率函数。
四 经验分布函数与直方图
1.样本的经验分布函数
(1)定义:设(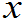 1,
1, 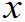 2,…
2,…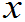 n)是来自总体X的一组样本值。将它们按由小到大排序为:
n)是来自总体X的一组样本值。将它们按由小到大排序为:
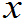 1*£
1*£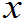 2*£…£
2*£…£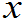 i*£…£
i*£…£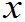 n*
对任意的实数
n*
对任意的实数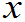 ,
,
定义函数:
Fn* (x)=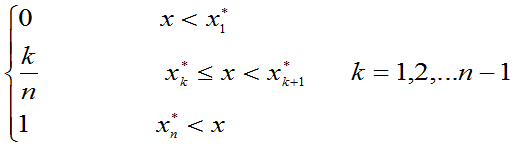


则称F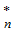 (
(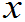 )为总体X的经验分布函数。
)为总体X的经验分布函数。
- 格列文科定理:
设总体X的分布函数、经验分布函数分别为F(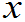 )、Fn*(
)、Fn*( ),则有:
),则有:
P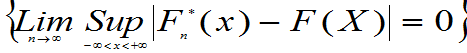 =1
=1
上式表明,当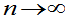 ,概率为1的有F
,概率为1的有F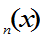 均匀地趋于F(
均匀地趋于F(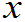 )。
)。
2总体的概率密度的估计¾直方图
(第一版) [p143 例6.3]
可以用SAS下的interactive data analysis 模块演示。
五 统计量与样本的数字特征
1 定义6.3: 设X1,X2,…,Xn是来自总体X的容量为n的样本,g(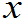 1,
1, 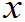 2,…,
2,…, 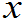 n)是定义在Rn或Rn子集上的普通函数。如果g中不含有任何未知量,则称g(X1,X2,…,Xn)为统计量。
n)是定义在Rn或Rn子集上的普通函数。如果g中不含有任何未知量,则称g(X1,X2,…,Xn)为统计量。
2.常用的统计量(样本的数字特征)
定义6.4:设X1,X2,…,Xn是来自总体X的样本,则称
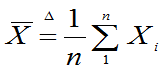 为样本均值
为样本均值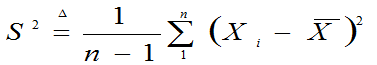
 为样本方差
为样本方差
 为样本k阶原点矩
为样本k阶原点矩
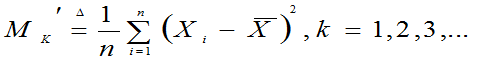 为样本k阶中心矩
为样本k阶中心矩
3.重要性质
定理6.1:设总体X不论服从什么分布,只要其二阶矩存在,即E(X)=μ、D(X)=б2都存在,则:
(1) E(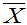 )=E(X)=μ
)=E(X)=μ
(2) D(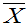 )=
)=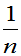 D(X)=
D(X)=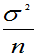
(3) E(S2)=D(X)=б2
重要恒等式: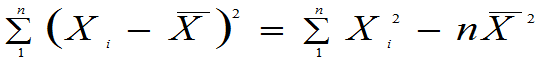
§6.2 抽样分布
统计量是样本的函数,它是一个随机变量。统计量的分布称为抽样分布。
一. 三个重要分布
(一)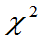 分布
分布
- 定义6.5:设X1,X2,…Xn相互独立,均服从N(0,1),则称随机变量
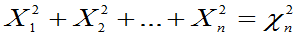 服从自由度为n的
服从自由度为n的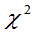 分布,记为
分布,记为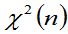 ,即:
,即: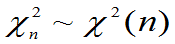 。
。
2.定理3.8: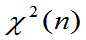 的概率密度为
的概率密度为
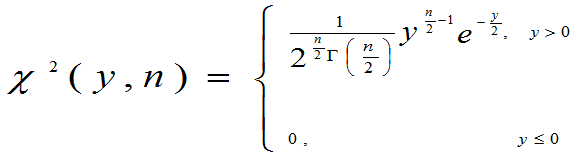
其中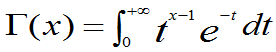
定理的说明见P146页。
3.图形.
分布函数图:
data Kf;
do x=0 to 30 by 0.1;
y= PROBCHI(x, 8);
output;
end;
run;
proc gplot data=kf;
plot y*x=1 ;
symbol1 v=none i=join r=1 c=black;
run;
密度函数图:n=1,5,15
data kf;
do y=0 to 20 by 0.1;
z0=(y**(-0.5)*exp(-y/2))/(2**0.5* GAMMA(0.5));
z1=(y**(1.5)*exp(-y/2))/(2**2.5* GAMMA(2.5));
z2=(y**(6.5)*exp(-y/2))/(2**7.5* GAMMA(7.5));
output;
end;
run;
proc gplot data=kf;
plot z0*y=1 z1*y=1 z2*y=1 /overlay ;
symbol1 v=none i=join r=1 c=black;
run;
求概率:
自由度为n=25, P{X<34.382}的概率这样求。
data;
p=PROBCHI(34.382,25); put p=;
run;
其它可类推。。
4.性质
①若 ,则E(
,则E(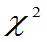 )=n,D(
)=n,D(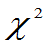 )=2n
)=2n

②若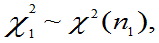
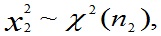 且它们相互独立,则
且它们相互独立,则
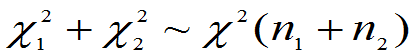
③若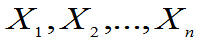 相互独立,均服从
相互独立,均服从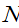 (μ,σ2),则
(μ,σ2),则
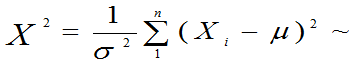
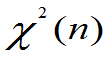
④总体X服从参数为λ的指数分布;X1,X2,…,Xn是来自该总体的样本.则:


(二).t分布
定义6.6:设X~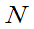 (0,1),Y~
(0,1),Y~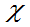 2(n)且它们相互独立,则称随机变量
2(n)且它们相互独立,则称随机变量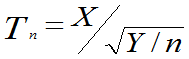 服从自由度为n的
服从自由度为n的 t分布,记为t(n),即
t分布,记为t(n),即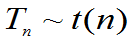 。
。
定理3.9: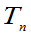 的概率密度为
的概率密度为
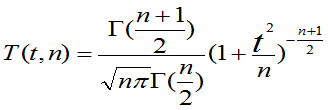 -∝<t<+∝
-∝<t<+∝
性质:
(1)t分布的密度是偶函数,图形为:
n=1, 10, 100时
data student;
do t=-3 to 3 by 0.01;
z1=(gamma(1)*(1+t**2)**(-1))/((3.1415926)**0.5*gamma(0.5));
z10=(gamma(5.5)*(1+t**2/10)**(-5.5))/((10*3.1415926)**0.5*gamma(5));
z100=(gamma(50.5)*(1+t**2/100)**(-50.5))/(100*(3.1415926)**0.5*gamma(50));
output;
end;
run;
proc gplot data=student;
plot z1*t=1 z10*t=1 z100*t=1/ overlay ;
symbol1 v=none i=join r=1 c=black;
run;
类似 (0,1)图形,n越大峰值越高。
(0,1)图形,n越大峰值越高。
分布函数图:n=10.
data t;
do x=-5 to 5 by 0.1;
y=PROBT(x, 10);
output;
end;
run;
proc gplot data=t;
plot y*x=1 ;
run;
(2)可证明
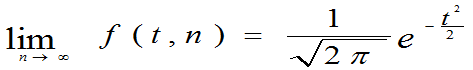
当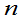 >45时,t分布与
>45时,t分布与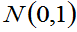 接近。
接近。
(3)当n>2时,E(T)=0,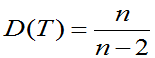 (证略)
(证略)
(三)F分布
定义6.7:设V~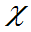 2(m),W~
2(m),W~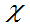 2(n),且它们相互独立,则称随机变量
2(n),且它们相互独立,则称随机变量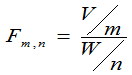 服从第一自由度为m、第二自由度为n的F分布,记为F(m,n),
服从第一自由度为m、第二自由度为n的F分布,记为F(m,n),
即
Fm,n~F(m,n)。
定理3.10:Fm,n为服从第一自由度为m,第二自由度为n
的F分布的随机变量, 则其密度函数为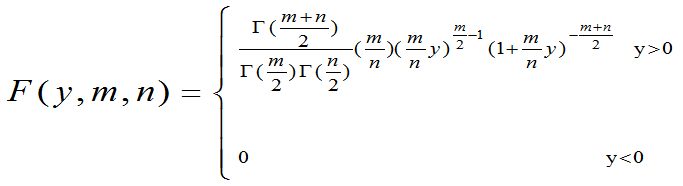
图形: 给定m,n可画出一个密度图形
密度函数图:
data f;
%macro a(m,n,x);
data a;
do y=0 to 2 by 0.01;
F&x=(gamma((&m+&n)/2)*(&m/&n)**(&m/2)*y**(&m/2-1))/(gamma(&m/2)*gamma(&n/2)*(1+(&m*y/&n))**(&m+&n)/2);
output;
end;
data F;
merge a f;
%mend a;
%a(10,25,1);
%a(10,5,2);
run;
proc gplot data=f;
plot F1*y=1 F2*y=1 / overlay ;
symbol1 v=none i=join r=1 c=black;
run;
易推知:
①若F~F(m,n),则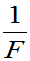 ~F(n,m)
~F(n,m)
②若X~t (n),则X2~F(1,n)
练习:书上P151有证明。
设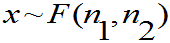 ,证明:
,证明: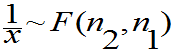 且
且
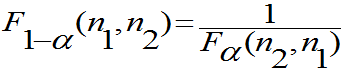
(注: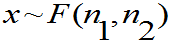 表示
表示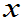 服从自由为
服从自由为 的F分布,
的F分布,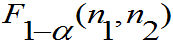 表示F分布的
表示F分布的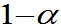 分位数。
分位数。
如:
data;
Q_F=FINV(0.95,12,9); put Q_F= ;
Q_F=FINV(1-0.95,12,9); put Q_F= ;
Run;
二.常用概率分布的分位数
定义6.8:
设X~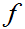 (x),对于给定的正数
(x),对于给定的正数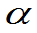
(0<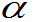 <1),若存在一个实数A
<1),若存在一个实数A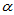 满足:
满足:
P{x>A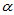 }=
}=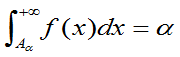
则称A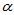 为X的上侧
为X的上侧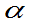 分位数,简称上
分位数,简称上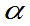 分位数;若X服从某分布,称A
分位数;若X服从某分布,称A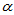 为某分布的上
为某分布的上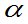 分位数。
分位数。
(1)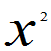 ~
~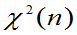
称满足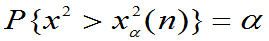 的数
的数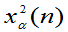 为自由度为n的
为自由度为n的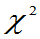 分布的上
分布的上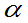 分位数。
分位数。
查表①P248 n≤45
②n>45时
注意所以类的统计分析软件不是这样定义的,只有一个分位数(实际上是下分位数的定义)
书上P147---148页,
data;
q1= CINV(1-0.005, 10); put q1=;
q2=CINV(1-0.01, 10); put q2=;
q3=CINV(1-.1,10); put q3=;
q4=CINV(1-.1,25); put q4=;
run;
q1=25.188179572
q2=23.209251159
q3=15.987179172
q4=34.381587018
自由度为n=25, P{X<34.382}的概率。
data;
p=PROBCHI(34.382,25); put p=;
run;
其它一些分布分位数求解
如前几章讲过的,对于正态分布有结果:
SAS的两种计算公式:
data;
p1=PROBNORM(1)-PROBNORM(-1); put p1=;
p2= PROBNORM(2)-PROBNORM(-2); put p2=;
p3= PROBNORM(3)-PROBNORM(-3); put p3=;
run;
p1=0.6826894921
p2=0.9544997361
p3=0.9973002039
data;
p1=2*PROBNORM(1)-1; put p1=;
p2=2*PROBNORM(2)-1; put p2=;
p3=2*PROBNORM(3)-1; put p3=;
run;
p1=0.6826894921
p2=0.9544997361
p3=0.9973002039
也可以验证数据,即以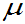 为中心,需要几倍的标准差
为中心,需要几倍的标准差 距离所构成的区间,其区间内的概率为上述所示。
距离所构成的区间,其区间内的概率为上述所示。
Data;
q1=abs(probit((1-0.6826894921)/2));put q1=;
q2=abs(probit((1-0.9544997361)/2));put q2=;
q3=abs(probit((1-0.9973002039)/2));put q3=;
run;
q1=0.9999999999
q2=2
q3=2.9999999959
data;
q1=probit(1-(1-0.6826894921)/2);put q1=;
q2=probit(1-(1-0.9544997361)/2);put q2=;
q3=probit(1-(1-0.9973002039)/2);put q3=;
run;
q1=0.9999999999
q2=2
q3=2.9999999959
注意: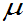 为中心,概率为90%,95%,98%,99%的区间,需要几倍的标准差
为中心,概率为90%,95%,98%,99%的区间,需要几倍的标准差 距离。
距离。
Data;
q1=abs(probit((1-0.9)/2));put q1=;
q2=abs(probit((1-0.95)/2));put q2=;
q3=abs(probit((1-0.98)/2));put q3=;
q3=abs(probit((1-0.99)/2));put q3=;
run;
q1=1.644853627
q2=1.9599639845
q3=2.326347874
q3=2.5758293035
比如,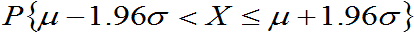
=0.95
等的结论也是常用的。几乎都成常识了。
data;
q1=exp(-1.65**2/2)/sqrt(2*(3.1415926));put q1=;
q2=PROBNORM(-1.65); put q2=;
aa=q1/q2;put aa=;
run;
还有如:
SAS FUNCTIONS: Quantile Functions
BETAINV(p,a,b) | returns a quantile from the beta distribution |
CINV(p,df<,nc>) | returns a quantile from the chi-squared distribution |
FINV(p,ndf,ddf<,nc>) | returns a quantile from the F distribution |
GAMINV(p,a) | returns a quantile from the gamma distribution |
PROBIT(p) | returns a quantile from the standard normal distribution |
TINV(p,df<,nc>) | returns a quantile from the t distribution |
可证明:n很大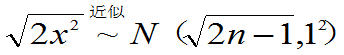

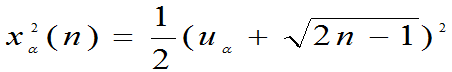
(2)T~t(n)
称满足P{T>tα(n)}=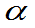 的数tα(n)为t(n)上
的数tα(n)为t(n)上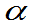 分位数。
分位数。
查表: ①n≤45时,直接查表。
②n>45时, 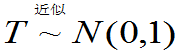 , tα(n)=uα
。
, tα(n)=uα
。
注意:T~t(n)的密度是偶函数。
称满足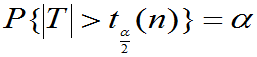 正数
正数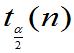 为分布的双侧
为分布的双侧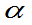 分位数。
分位数。
易知: 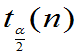 查表可得,且
查表可得,且
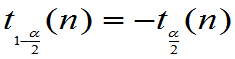
同样标准正态分布有:
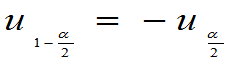 。
。
例:n=20的t分布,求其0.1的上分位数,有
data ;
q=TINV(1-0.1,5); put q=;
q=TINV(1-0.1,10); put q=;
q=TINV(1-0.1,20); put q=;
q=TINV(1-0.1,50); put q=;
q=TINV(1-0.1,100); put q=;
q=TINV(1-0.1,200); put q=;
qnorm=(probit(1-0.1));put qnorm=;
run;
q=1.4758840488
q=1.3721836411
q=1.325340707
q=1.2987136942
q=1.2900747613
q=1.285798794
qnorm=1.2815515655
对于概率:我们看一下当n很大时,t(n)和标准正态分布的近似性。
data;
prob_t=PROBT(1.3, 5); put prob_t=;
prob_t=PROBT(1.3, 10); put prob_t=;
prob_t=PROBT(1.3, 20); put prob_t=;
prob_t=PROBT(1.3, 50); put prob_t=;
prob_t=PROBT(1.3, 100); put prob_t=;
prob_t=PROBT(1.3, 200); put prob_t=;
Prob_n=PROBNORM(1.3);put Prob_n=;
Run;
(3)若F~F(m ,n)
称满足P{F>Fα(m,n)}=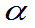 的数Fα(m,n)为F分布的上
的数Fα(m,n)为F分布的上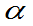 分位数。
分位数。
查表:①表中有的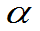 可直接查表P250
可直接查表P250
②表中没有的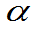
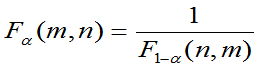
三.正态总体的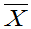 、S2的分布
、S2的分布
定理6.2:(费歇(Fisher)定理)
设总体X~N(μ,σ2),X1,X2,…,Xn为来自总体X的样本,其样本均值和样本方差分别记为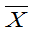 和S2。
和S2。
则有(1) 与S2相互独立。
与S2相互独立。
(2)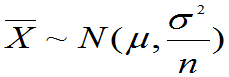
(3)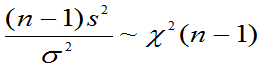
证明见书P150
推论1: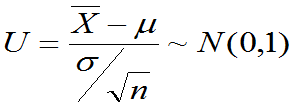
例:总体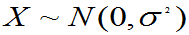 ,问
,问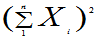 与
与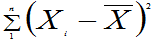 是否独立?
是否独立?
又问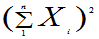 +
+ 服从什麽分布?
服从什麽分布?
推论2:
定理6.3:设有两个总体: 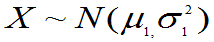 ,其样本为X1,X2,… ,Xn,样本均值
,其样本为X1,X2,… ,Xn,样本均值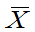 ,样本方差
,样本方差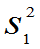 总体
总体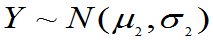 ,其样本为
,其样本为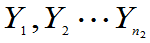 ,样本均值为
,样本均值为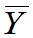 ,样本方差为
,样本方差为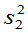 ,且两个样本相互独立.则有:
,且两个样本相互独立.则有:
(1) 
(2) 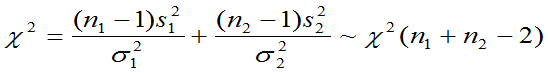
(3) 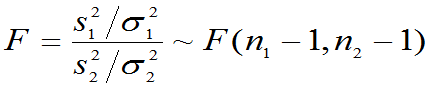
特别当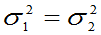 时,
时,
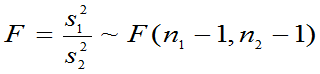
(4)当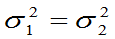 时,
时,
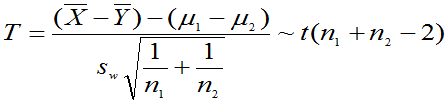 ,
,
其中
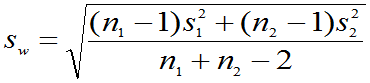
例:设总体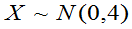 ,
,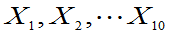 为来自总体的样本。令
为来自总体的样本。令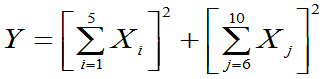 ,
,
试确定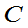 使
使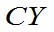 服从
服从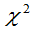 分布,并指出其自由度。
分布,并指出其自由度。
本章习题:1~8
附加:
设总体X服从贝努里b(1,p)分布,其中p是未知参数。X=(X1,…X5)是从中抽取的一简单随机子样。写出它的子样空间和X的概率分布;



