§4 二次曲线的直径
一 定义:
引理:二次曲线的沿方向X:Y的所有弦的中点轨迹是一直线:
X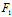 (x,y)+Y
(x,y)+Y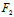 (x,y)=0 即
(x,y)=0 即
(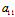 X+
X+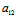 Y)x+(
Y)x+(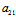 X+
X+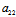 Y)y+
Y)y+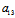 X+
X+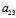 Y=0 (1)
Y=0 (1)
事实上,任取沿X:Y的弦的中点 (
(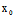 ,
,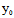 ),则该弦所在直线l:
),则该弦所在直线l:
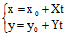 ,弦的端点
,弦的端点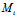 (
( +
+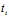 X ,
X ,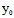 +
+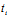 Y) ,i=1,2 中
Y) ,i=1,2 中 ,
,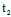 应满足
应满足
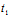 +
+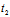 =0 ,
=0 ,
∴X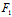 (
(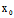 ,
,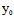 )+Y
)+Y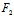 (
( ,
, )=0
)=0
反之,若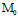 (
( ,
,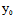 )的坐标满足上述等式,任取过
)的坐标满足上述等式,任取过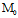 且沿X:Y的弦
且沿X:Y的弦
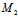 ,
,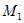
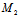 所在直线 l:
所在直线 l: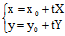 若令
若令 (
(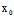 +
+ X,
X,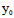 +
+ Y),i=1,2,则
Y),i=1,2,则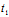 +
+ =0
=0
∴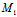
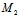 的中点坐标
的中点坐标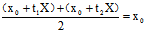
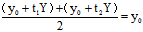
即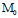 是弦
是弦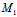
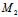 的中点,最后证(1)表示一直线,因若不然
的中点,最后证(1)表示一直线,因若不然
(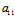 X+
X+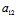 Y)X+(
Y)X+(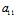 X+
X+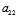 Y)Y=0
Y)Y=0
即 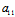 X²+2
X²+2 XY+
XY+ Y²=0 这与X:Y为非渐近方向不符。
Y²=0 这与X:Y为非渐近方向不符。
定义:称方程(1)所表示的直线为二次曲线F(x,y)=0的共轭于方向X:Y的直径。
注:1°上述定义中的X:Y即可以为非渐近方向,也可以为渐近方向。当X:Y为非渐近方向时,直径(1)有明确的几何意义——平行于X:Y的所有弦的中点轨迹;当X:Y为渐近方向时,由于X:Y=-(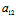 X+
X+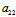 Y):(
Y):( X+
X+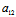 Y)
Y)
∴直径(1)沿渐近方向X:Y
2°当二次曲线有中心时,则直径(1)过所有中心,∴线心曲线仅有一直径。
3°渐近线是直径的特例
4°中心二次曲线的所有直径形成的以中心为束心的有心直线束;无心二次曲线的所有直径形成平行于渐近方向的平行直线束。
事实上,由于直径(1)的方程为 X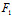 (x,y)+Y
(x,y)+Y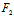 (x,y)=0
(x,y)=0
当曲线为中心曲线时,二直线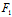 (x,y)=0与
(x,y)=0与 (x,y)=0有唯一交点。而对无心曲线,二直线
(x,y)=0有唯一交点。而对无心曲线,二直线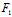 (x,y)=0与
(x,y)=0与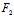 (x,y)=0为平行(非重合)直线,且其方向
(x,y)=0为平行(非重合)直线,且其方向
X:Y=-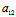 :
: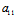 是渐近方向。
是渐近方向。
例:求二次曲线x²-2xy+y²+2x-2y=0的共轭于非渐近方向X:Y的直径。
解:略。
二 共轭方向与共轭直径:
定义1:对二次曲线F(x,y)=0,若二方向X:Y与X′:Y′满足
X′:Y′=-( X+
X+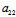 Y):(
Y):( X+
X+ Y)
Y)
(等价地:X:Y=-(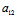 X′+
X′+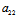 Y′):(
Y′):(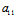 X′+
X′+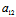 Y′))
Y′))
则称X:Y与X′:Y′是一对共轭方向
注:1°共轭于方向X:Y的直径(1)是沿X:Y的共轭方向的;
2°实方向的共轭方向仍是实的,共轭于实方向的直径(1)也是实的;
3°对于中心二次曲线,非渐近方向的共轭方向依然是非渐近方向;对于非中心二次曲线,任意方向的共轭方向均为渐近方向
事实上,1°,2°显然,对于3°,设X:Y的共轭方向为X′:Y′,则
Φ(X′,Y′)=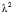 [
[ (
( X+
X+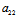 Y)
Y) -2
-2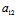 (
(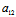 X+
X+ Y)(
Y)(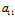 X+
X+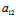 Y)+
Y)+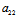 (
(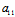 X+
X+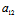 Y)
Y) ]
]
=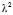
 Φ(X,Y)
Φ(X,Y)
定义2:对中心二次曲线F(x,y)=0,沿一对共轭方向的二直线称为一对共轭直径。
推论:斜率为k,k′的一对直径为共轭直径〈═〉k,k′满足
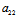 kk′+
kk′+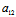 (k+k′)
(k+k′)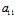 =0
=0
事实上,设二直径的方向为X:Y喝X′:Y′,则二直径共轭〈═〉
X′:Y′=-(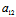 X+
X+ Y):(
Y):(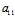 X+
X+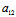 Y)
Y)
〈═〉(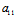 X+
X+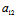 Y)X′+(
Y)X′+(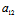 X+
X+ Y)Y′=0
Y)Y′=0
〈═〉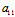 XX′+
XX′+ (X′Y+XY′)+
(X′Y+XY′)+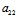 YY′=0
YY′=0
〈═〉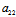
 +
+ (
(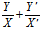 )+
)+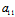 =0
=0
〈═〉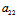 kk′+
kk′+ (k+k′)+
(k+k′)+ =0
=0
例:考察椭圆、双曲线共轭直径的分布情况
解:对于椭圆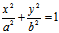 ,其一对共轭直径的斜率k,k′应满足
,其一对共轭直径的斜率k,k′应满足
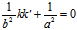 即 kk′=-
即 kk′=-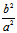 <0
<0
可见一对共轭直径分别在一,二象限,而且当一直径的斜率k(>0)逐渐扩大时,
其共轭直径的斜率k′(<0)亦逐渐扩大,亦即当直径I(k>0)按逆时针方向旋转
时,其共轭直径II(k′<0)也按逆时针方向旋转。
对双曲线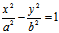 ,其一对共轭直径的斜率k,k′应满足
,其一对共轭直径的斜率k,k′应满足
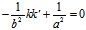 即
即
kk′=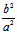 >0
>0
可见一对共轭直径在同在一象限内,且因0<k< 时,k′>
时,k′> ,∴一对共轭直径分别在渐近线的两侧,当直径I(k<
,∴一对共轭直径分别在渐近线的两侧,当直径I(k<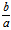 )按逆时针靠近渐近线时,其共轭直径
)按逆时针靠近渐近线时,其共轭直径
II(k′>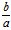 )则按顺时针靠近渐近线。
)则按顺时针靠近渐近线。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号