§9 三矢量的混合积
定义1 给定空间的三个矢量
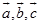 ,我们
,我们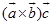 叫做三矢量
叫做三矢量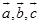 的混合积,记做
的混合积,记做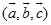 或
或 .
.
定理1 三个不共面矢量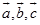 的混合积的绝对值等于以
的混合积的绝对值等于以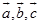 为棱的平行六面体的体积
为棱的平行六面体的体积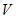 ,并且当
,并且当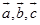 构成右手系时混合积为正;当
构成右手系时混合积为正;当 构成左手系时混合积为负.
构成左手系时混合积为负.
证 由于矢量 不共面,所以把它们归结到共同的试始点
不共面,所以把它们归结到共同的试始点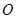 可构成以
可构成以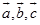 为棱的平行六面体,它的底面是以
为棱的平行六面体,它的底面是以 为边的平行四边形,面积为
为边的平行四边形,面积为 ,它的高为
,它的高为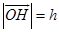 ,体积是
,体积是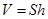 .
.
根据数性积的定义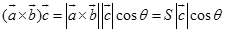 ,
,
其中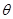 是
是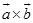 与
与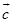 的夹角.
的夹角.
当 构成右手系时,
构成右手系时,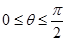 ,
, ,因而可得
,因而可得
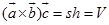 .
.
当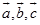 构成左手系时,
构成左手系时, ,
, ,因而可得
,因而可得
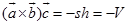 .
.
定理2 三矢量
 共面的充要条件是
共面的充要条件是 .
.
证 若三矢量
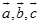 共面,由定理1.9.1知
共面,由定理1.9.1知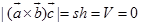 ,所以
,所以 ,从而
,从而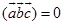 .
.
反过来,如果 ,即
,即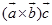 ,那么根据定理1.7.1有
,那么根据定理1.7.1有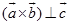 ,另一方面,有矢性积的定义知
,另一方面,有矢性积的定义知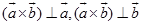 ,所以
,所以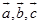 共面.
共面.
定理3 轮换混合积的三个因子,并不改变它的值;对调任何俩因子要改变混合积符号,即
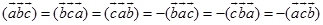 .
.
证 当 共面时,定理显然成立;当
共面时,定理显然成立;当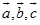 不共面时,混合积的绝对值等于以
不共面时,混合积的绝对值等于以 为棱的平行六面体的体积
为棱的平行六面体的体积 ,又因轮换
,又因轮换 的顺序时,不改变左右手系,因而混合积不变,而对调任意两个之间的顺序时,将右手系变为左,而左变右,所以混合积变号.
的顺序时,不改变左右手系,因而混合积不变,而对调任意两个之间的顺序时,将右手系变为左,而左变右,所以混合积变号.
推论1
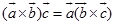 .
.
定理4
设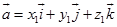 ,
,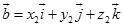 ,
, ,那么
,那么
 .
.
证 由矢量的矢性积的计算知
 ,
,
再根据矢量的数性积得
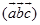 =
=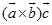 =
=
= .
.
推论2 三矢量 共面的充要条件是
共面的充要条件是
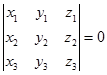 .
.




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步