§8 两矢量的矢量积
定义1 设矢量c是由两个矢量a与b按下列方式定出:c的模 |c|=|a||b|sin q , 其中q 为a与b间的夹角;c的方向垂直于a与b所决定的平面, c的指向按右手规则从a转向b来确定,我们把这样的矢量c叫做矢量a与b的矢量积, 记作a´b, 即
c=a´b.
从定义知矢量积有下列性质:
(1) a´a=0
(2) 对于两个非零矢量a,b, 如果a´b=0, 则a//b;反之, 如果a//b, 则a´b = 0.
定理1 两矢量a与b共线的充要条件是a´b=0.
证 当a与b共线时,由于sin(a、b)=0,所以|a´b|=|a||b| sin(a、b)=0,从而a´b=0;反之,当a´b=0时,由定义知,a =0 ,或b =0,或a//b,因零矢可看成与任矢量都共线,所以总有a//b,即a与b共线.
定理2 矢量积满足下面的运算律:
(1) 交换律 a´b=-b´a,
(2) 分配律 (a+b)´c=a´c+b´c,
(3) 数因子的结合律 (la)´b=a´(lb)=l(a´b) (l为数).
证 (略).
定理3 设a = ax i + ay j + az k, b = bx i + by j + bz k,则 a´b=(aybz -azby)i+(azbx -axbz)j+(axby -aybx)k.
证 由矢量积的运算律可得
a´b=(ax i+ay j+az k)´(bx i+by j +bz k)
=axbx i´i+axby i´j +axbz i´k
+aybx j´i+ayby j´j+aybz j´k
+azbx k´i+azby k´ +azbz k´k.
由于 i´i=j´j=k´k=0, i´j=k, j´k=i, k´i=j,
所以 a´b=(aybz -azby)i+(azbx -axbz)j+(axby -aybx)k.
为了邦助记忆, 利用三阶行列式符号, 上式可写成
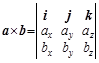 =aybzi+azbxj+axbyk-aybxk-axbzj-azbyi
=aybzi+azbxj+axbyk-aybxk-axbzj-azbyi
=(ay bz -az by)i+(az bx -ax bz)j+(ax by -ay bx)k. .
例1 设a=(2, 1, -1), b=(1, -1, 2), 计算a´b .
解
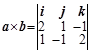 2i-j-2k-k-4j-i
=i-5j -3k.
2i-j-2k-k-4j-i
=i-5j -3k.
例2 已知三角形ABC的顶点分别是A (1, 2, 3)、B (3, 4, 5)、C (2, 4, 7), 求三角形ABC的面积.
解 根据向量积的定义, 可知三角形ABC的面积
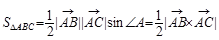 .
.
由于 =(2, 2, 2),
=(2, 2, 2), 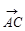 =(1, 2, 4), 因此
=(1, 2, 4), 因此


 =4i-6j+2k.
=4i-6j+2k.
于是 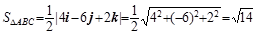 .
.
例3 设刚体以等角速度w 绕l 轴旋转, 计算刚体上一点M的线速度.
解 刚体绕l 轴旋转时, 我们可以用在l 轴上的一个向量n表示角速度, 它的大小等于角速度的大小, 它的方向由右手规则定出: 即以右手握住l 轴, 当右手的四个手指的转向与刚体的旋转方向一致时, 大姆指的指向就是n的方向.
设点M到旋转轴l的距离为a
, 再在l轴上任取一点O作向量r
=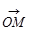 , 并以q 表示n与r的夹角, 那么
, 并以q 表示n与r的夹角, 那么
a = |r| sinq .
设线速度为v, 那么由物理学上线速度与角速度间的关系可知, v的大小为
|v| =| n|a = |n||r| sinq
v的方向垂直于通过M点与l轴的平面, 即v垂直于n与r, 又v的指向是使n、r、v符合右手规则. 因此有
v = n´r.




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步