第一章 矢量与坐标
本章教学目的:通过本章学习,使学生掌握矢量及其运算的概念,熟练掌握线性运算和非线性运算的基本性质、运算规律和分量表示,会利用矢量及其运算建立空间坐标系和解决某些几何问题,为以下各章利用代数方法研究空间图形的性质打下基础。
本章教学重点:(1)矢量的基本概念和矢量间关系的各种刻划;
(2)矢量的线性运算、积运算的定义、运算规律及分量表示。
本章教学难点:(1)矢量及其运算与空间坐标系的联系;
(2)矢量的数量积与矢量积的区别与联系;
(3)矢量及其运算在平面、立体几何中的应用。
本章教学内容:
§1 矢量的基本概念
- 定义:既有大小又有方向的量称为矢量,如力、速度、位移等。
- 表示:在几何上,用带箭头的线条表示矢量,箭头表示矢量的方向,线条长度代表矢量的大小;矢量的大小又叫矢量的摸(长度)。
始点为A,终点为B的矢量,记作
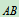 ,其摸记做
,其摸记做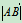 。
。
注:为方便起见,今后除少数情形用矢量的始、终点字母标记矢量外,我们一般用小写黑体字母a、b、c……标记矢量,而用希腊字母λ、μ、ν……标记数量。
三、两种特殊矢量:
- 零矢量:模等于0的矢量为零矢量,简称零矢,以0记之。
注:零矢量是唯一方向不定的矢量。
2、位矢量:模等于1的矢量称为单位矢量,简称单位矢。特别地,与非0矢量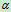 同向的单位矢称为
同向的单位矢称为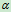 的单位矢,记作
的单位矢,记作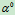 。
。
四、矢量间的几种特殊关系:
1、平行(共线):矢量a平行于矢量b,意即a所在直线平行于b所在直线,记作a∥b,规定:零矢量平行于任何矢量,
2、相等:矢量a等于矢量b,意即  ,记作a=b。
,记作a=b。
规定:所有零矢均相等。
注:二矢量相等与否,仅取决于它们的模与方向,而与其位置无关,这种与位置无关的矢量称为自由矢量。
3、反矢量:与矢量 模相等但方向相反的矢量称为
模相等但方向相反的矢量称为 的反矢量,记作
的反矢量,记作 ,显然
,显然

 ,零矢量的反矢量还是其自身。
,零矢量的反矢量还是其自身。
4、共面矢量:平行于同一平面的一组矢量称为共面矢量,易见,任两个矢量总是共面的,零矢量与任何共面矢量组共面。
注:应把矢量与数量严格区别开来:
①矢量不能比较大小,如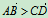 没有意义;
没有意义;
②矢量严禁除法运算,如 此类式子不允许出现。
此类式子不允许出现。




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步