例10.4在平面机构中,直角三角板ABD的两直角边长为 ,
,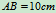 ,A、B为光滑铰接,
,A、B为光滑铰接,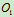 、
、 为两固定铰支座,
为两固定铰支座,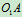 杆以
杆以 绕
绕 轴匀速转动,设
轴匀速转动,设
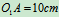 ,
,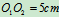 ,图示瞬时
,图示瞬时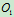 、A、D在同一铅垂线上,求该瞬时D点的速度和杆的角速度。
、A、D在同一铅垂线上,求该瞬时D点的速度和杆的角速度。

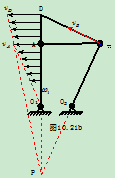
解:1.分析运动
 、
、 杆作定轴转动,
杆作定轴转动,
ABD作平面运动
2. 分析速度
 :
:
ABD: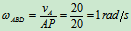
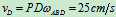

 :
: 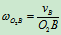
例10.5绕线轮半径为R,其凸沿半径为r,绕线之线点B沿水平方向抽出之速度为u,使轮沿水平线纯滚动。试求滚轮上1、2、3点的速度。

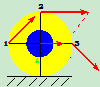
解: 1 分析运动
2 速度分析
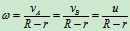
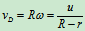
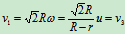

问:线头与水平线夹角为多少度时,轮O向左滚动?(演示不断改变线头B与水平线夹角拉轮子滚动)
(图10.22)
例10.6平面机构如图10.23所示,已知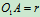 ,以
,以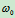 匀速转动,
匀速转动,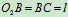 ,图示时
,图示时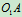 水平,
水平,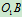 在铅直方向,
在铅直方向,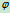 、
、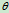 均为已知,求该瞬时,
均为已知,求该瞬时, 杆的角速度和滑块C的速度。
杆的角速度和滑块C的速度。

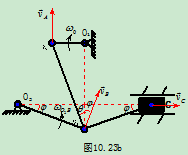
解:1 分析运动
 、
、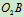 定轴转动
定轴转动
AB、BC杆平面运动
2.分析运动
 :
: 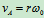
AB: 
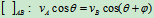
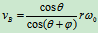
 :
: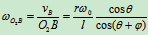
BC: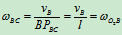

三、平面图形的角加速度及图形上各点的加速度分析
1 基点法
设已知A点加速度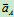 和图形的角速度
和图形的角速度 ,角加速度
,角加速度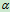 ,求任一点B的加速度平面
,求任一点B的加速度平面
运动随A点平动+相对A点转动
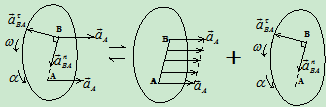
B点加速度: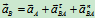 (10.6)
(10.6)
其中 ,方向垂直于AB,
,方向垂直于AB, ,方向由B指向A。
,方向由B指向A。
式(10.6)也只能求解2个未知量。
式(10.6)也可用矢量求导的方法得到,参看图10.10,有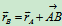
求一次导 
求二次导 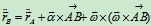
其中 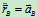 ,
, 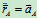 ,
, 
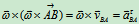
∴
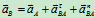
例10.7靠在直角墙上的杆AB长为 ,由铅垂位置在铅垂面内滑下,如图所示。当
,由铅垂位置在铅垂面内滑下,如图所示。当 时,
时,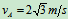 ,
,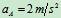 方向如图所示。求该瞬时B点的加速度及AB杆的角加速度。
方向如图所示。求该瞬时B点的加速度及AB杆的角加速度。
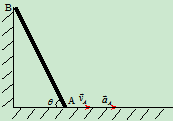
解:1. 运动分析
2. 分析速度
AB作平面运动,
由瞬心法求得
 :
:

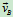
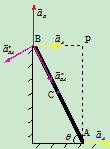
3.分析加速度
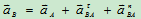 (方向如图25)
(方向如图25)
其中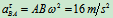
 :
: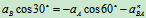

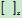 :
: 

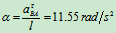
问:若求AB中点C的加速度呢?
例10.8半径为R的圆盘沿直线轨道作纯滚动,如图26所示,设图示瞬时轮心的速度为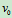 ,加速度为
,加速度为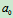 ,方向如图所示。试求该瞬时轮沿上A、B、C、D点的加速度。
,方向如图所示。试求该瞬时轮沿上A、B、C、D点的加速度。

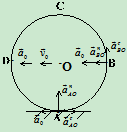
解:1 分析运动
轮O作纯滚动,图示时 ,
,
A点为速度瞬心
因为轮运动过程中,轮心O到瞬心点距离始终为定长R,如把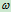 、
、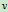 看成时间
看成时间 的函数关系,上式仍成立,因而有
的函数关系,上式仍成立,因而有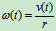 对此式求导有
对此式求导有
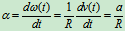
当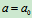 时,
时,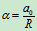 转向为逆时针
转向为逆时针
2.分析加速度

其中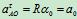 ,
,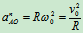
(速度瞬心的加速度不为零)
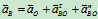
其中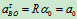 ,
,
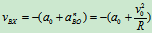 ,
,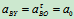
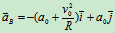
同理可求得


例10.9在图27所示机构中,曲柄OA以 绕O轴匀速转动,通过连杆AN带动轮B沿水平直线纯滚动,设
绕O轴匀速转动,通过连杆AN带动轮B沿水平直线纯滚动,设 ,
, ,轮半径为R,求图示OA杆铅直时,轮上最高点D的速度、加速度。
,轮半径为R,求图示OA杆铅直时,轮上最高点D的速度、加速度。


解:1. 分析运动:
OA杆定轴转动,
AB杆、B轮昀作平面运动
2.分析速度
OA: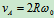
AB:∵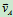 ∥
∥ ,且
,且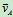 AB
AB
AB瞬时平动∴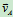 =
=
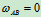
轮B:
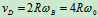
3.加速度分析
OA: 
AB:  其中
其中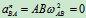
由图27 可求得 (
( )
)
B轮: 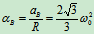
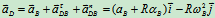



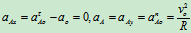




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步