§6 行列式按一行(列) 展开
在§4看到,对于 级行列式,有
级行列式,有
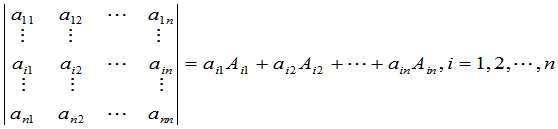 . (1)
. (1)
现在来研究这些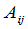 ,
, 究竟是什么.
究竟是什么.
三级行列式可以通过二级行列式表示:
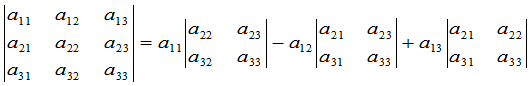 . (2)
. (2)
定义7 在行列式
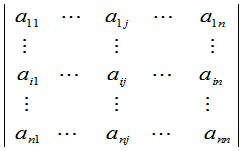
中划去元素 所在的第
所在的第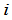 行与第
行与第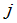 列,剩下的
列,剩下的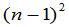 个元素按原来的排法构成一个
个元素按原来的排法构成一个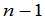 级行列式
级行列式
 (3)
(3)
称为元素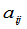 的余子式,记作
的余子式,记作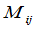
下面证明
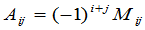 . (4)
. (4)
为此先证明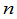 级行列式与
级行列式与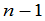 级行列式的下面这个关系,
级行列式的下面这个关系,
 . (5)
. (5)
定义8 上面所谈到的 称为元素
称为元素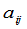 的代数余子式.
的代数余子式.
这样,公式(1)就是说,行列式等于某一行的元素分别与它们代数余子式的乘积之和.在(1)中,如果令第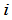 行的元素等于另外一行,譬如说,第
行的元素等于另外一行,譬如说,第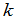 行的元素,也就是
行的元素,也就是
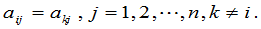
于是
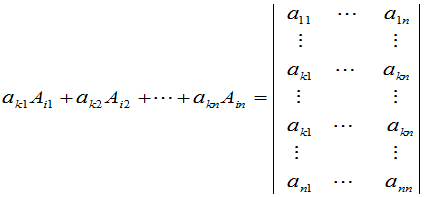
右端的行列式含有两个相同的行,应该为零,这就是说,在行列式中,一行的元素与另一行相应元素的代数余子式的乘积之和为零.
定理3 设

 表示元素
表示元素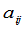 的代数余子式,则下列公式成立:
的代数余子式,则下列公式成立:

 (6)
(6)
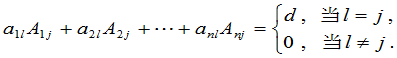 (7)
(7)
用连加号简写为

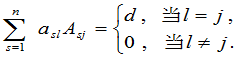
在计算数字行列式时,直接应用展开式(6)或(7)不一定能简化计算,因为把一个 级行列式的计算换成
级行列式的计算换成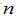 个(
个( )级行列式的计算并不减少计算量,只是在行列式中某一行或某一列含有较多的零时,应用公式(6)或(7)才有意义.但这两个公式在理论上是重要的.
)级行列式的计算并不减少计算量,只是在行列式中某一行或某一列含有较多的零时,应用公式(6)或(7)才有意义.但这两个公式在理论上是重要的.
例1 计算行列式
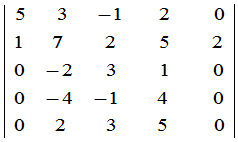
例2 行列式
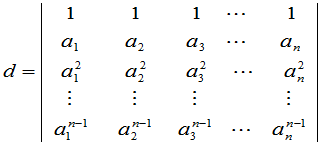 (8)
(8)
称为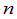 级的范德蒙德(Vandermonde)行列式.证明对任意的
级的范德蒙德(Vandermonde)行列式.证明对任意的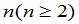 ,
,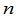 级范德蒙德行列式等于
级范德蒙德行列式等于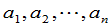 这
这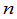 个数的所有可能的差
个数的所有可能的差 的乘积.
的乘积.
用连乘号,这个结果可以简写为
 .
.
由这个结果立即得出,范德蒙德行列式为零的充要条件是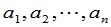 这
这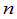 个数中至少有两个相等.
个数中至少有两个相等.
例3 证明
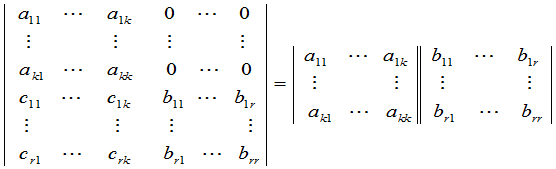
§7 克拉默(Cramer)法则
现在应用行列式解决线性方程组的问题.在这里只考虑方程个数与未知量个数相等的情形.
定理4 如果线性方程组
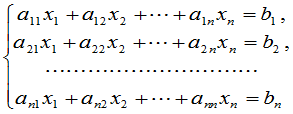 (1)
(1)
的系数矩阵
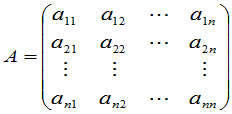 (2)
(2)
的行列式
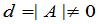
那么线性方程组(1)有解,并且解是唯一的,解可以通过系数表为
 , (3)
, (3)
其中 是把矩阵
是把矩阵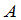 中第
中第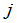 列换成常数项
列换成常数项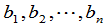 所成的矩阵的行列式,即
所成的矩阵的行列式,即
 (4)
(4)
定理中包含着三个结论:1)方程组有解;2)解是唯一的;3)解由公式(3)给出.这三个结论是有联系的,因此证明的步骤是:
1. 把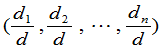 代入方程组,验证它确是解.
代入方程组,验证它确是解.
2. 假如方程组有解,证明它的解必由公式(3)给出.
定理4通常称为克拉默法则.
例1 解方程组
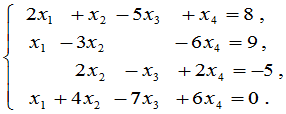
应该注意,定理4所讨论的只是系数矩阵的行列式不为零的方程组,它只能应用于这种方程组;至于方程组的系数行列式为零的情形,将在下一章的一般情形中一并讨论.
常数项全为零的线性方程组称为齐次线性方程组.显然齐次方程组总是有解的,因为 就是一个解,它称为零解.对于齐次线性方程组,我们关心的问题常常是,它除了零解以外,还有没有其它解,或者说,它有没有非零解.对于方程个数与未知量个数相同的齐次线性方程组,应用克拉默法则就有
就是一个解,它称为零解.对于齐次线性方程组,我们关心的问题常常是,它除了零解以外,还有没有其它解,或者说,它有没有非零解.对于方程个数与未知量个数相同的齐次线性方程组,应用克拉默法则就有
定理5 如果齐次线性方程组
 (10)
(10)
的系数矩阵的行列式 ,那么它只有零解.换句话说,如果方程组(10)有非零解,那么必有
,那么它只有零解.换句话说,如果方程组(10)有非零解,那么必有 .
.
例2 求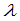 在什么条件下,方程组
在什么条件下,方程组

有非零解.
克拉默法则的意义主要在于它给出了解与系数的明显关系,这一点在以后许多问题的讨论中是重要的.但是用克拉默法则进行计算是不方便的,因为按这一法则解一个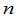 个未知量
个未知量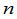 个方程的线性方程组就要计算
个方程的线性方程组就要计算 个
个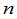 级行列式,这个计算量是很大的.
级行列式,这个计算量是很大的.
§8 拉普拉斯(Laplace)定理 行列式的乘法规则
一、拉普拉斯定理
定义9 在一个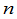 级行列式
级行列式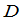 中任意选定
中任意选定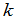 行
行 列(
列(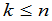 ),位于这些行和列的交点上的
),位于这些行和列的交点上的 个元素按照原来的次序组成一个
个元素按照原来的次序组成一个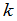 级行列式
级行列式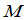 ,称为行列式
,称为行列式 的一个
的一个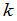 级子式.在
级子式.在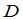 中划去这
中划去这 行
行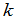 列后余下的元素按照原来的次序组成的
列后余下的元素按照原来的次序组成的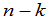 级行列式
级行列式 称为
称为 级子式
级子式 的余子式.
的余子式.
从定义立刻看出,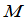 也是
也是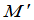 的余子式.所以
的余子式.所以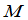 和
和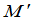 可以称为
可以称为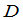 的一对互余的子式.
的一对互余的子式.
例1 在四级行列式
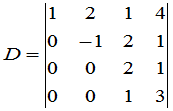
中选定第一、三行,第二、四列得到一个二级子式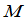 :
:
 ,
,
 的余子式为
的余子式为
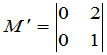 .
.
例2 在五级行列式
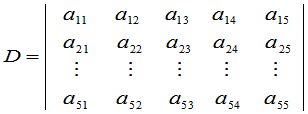
中

和

是一对互余的子式.
定义10 设 的
的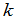 级子式
级子式 在
在 中所在的行、列指标分别是
中所在的行、列指标分别是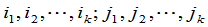 ,则
,则 的余子式
的余子式 前面加上符号
前面加上符号 后称做
后称做 的代数余子式.
的代数余子式.
因为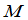 与
与 位于行列式
位于行列式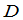 中不同的行和不同的列,所以有下述
中不同的行和不同的列,所以有下述
引理 行列式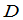 的任一个子式
的任一个子式 与它的代数余子式
与它的代数余子式 的乘积中的每一项都是行列式
的乘积中的每一项都是行列式 的展开式中的一项,而且符号也一致.
的展开式中的一项,而且符号也一致.
定理6(拉普拉斯定理) 设在行列式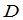 中任意取定了
中任意取定了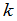 (
(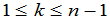 )个行.由这
)个行.由这 行元素所组成的一切
行元素所组成的一切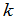 级子式与它们的代数余子式的乘积的和等于行列式
级子式与它们的代数余子式的乘积的和等于行列式 .
.
例3 利用拉普拉斯定理计算行列式

从这个例子来看,利用拉普拉斯定理来计算行列式一般是不方便的.这个定理主要是理论方面的应用.
二、行列式的乘积法则
定理7 两个 级行列式
级行列式
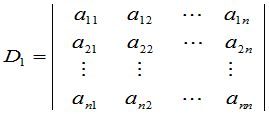
和
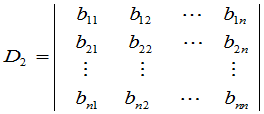
的乘积等于一个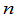 级行列式
级行列式
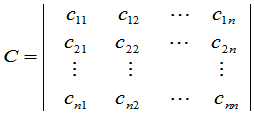 ,
,
其中 是
是 的第
的第 行元素分别与
行元素分别与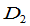 的第
的第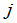 列的对应元素乘积之和:
列的对应元素乘积之和:
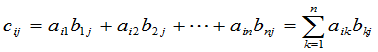 .
.
这个定理也称为行列式的乘法定理.它的意义到第四章§3中就完全清楚了.
第二章 行列式(小结)
一、行列式理论
1.  级排列
级排列
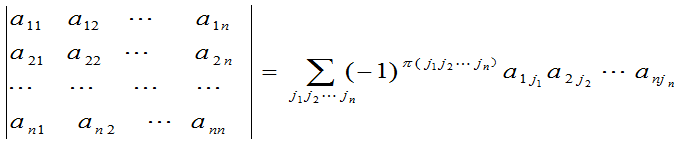 (1) 基本概念:排列,反序,反序数,排列的奇偶性
(1) 基本概念:排列,反序,反序数,排列的奇偶性
(2) 主要结论
 级排列共有
级排列共有 个,其中奇偶排列各占一半
个,其中奇偶排列各占一半
对换改变排列的奇偶性
任意一个 级排列都可以经过一些对换变成自然顺序,并且所作对换的个数与这个排列有相同的奇偶性
级排列都可以经过一些对换变成自然顺序,并且所作对换的个数与这个排列有相同的奇偶性
2.  级行列式的概念
级行列式的概念
其中
3. 行列式的性质
(1) 有关行列式的转置
行列互换,行列式不变
(2) 有关行(列)的变换
互换行(列),行列式反号
用一个数乘某行(列),就等于用这个数乘这个行列式
把某行(列)的倍数加到另一行(列),行列式不变
(3) 有关按行(列)分解为两个行列式的和
如果某行(列)是两组数的和,那么行列式可以写成两个行列式的和,这两个行列式的这一行(列)分别是第一组数与第二组数,而其它各行(列)都与原行列式相同
(4) 有关行列式等于零
两行(列)成比例,行列式等于零
4. 行列式依行依列展开
(1) 基本概念:子式,余子式,代数余子式
(2) 主要公式

5. 克拉默规则
若线性方程组
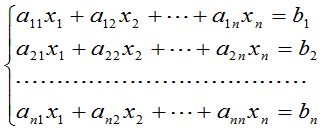
的行列式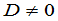 ,则它有唯一解
,则它有唯一解
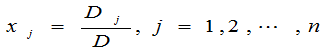
其中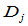 是把
是把 的第
的第 列换成常数项
列换成常数项 所得的行列式
所得的行列式
二、行列式计算方法
1. 定义法 本章主要内容的内在联系:
2. 化为三角形行列式的方法
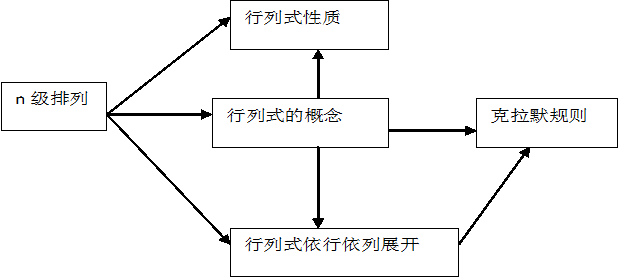 3. 化为范得蒙行列式的方法
3. 化为范得蒙行列式的方法
4. 拆行(列)法
5. 降级法
6. 加边法
7. 数学归纳法
8. 递推法
9. 因式分解法
二、行列式计算方法
- 定义法
2. 化为三角形行列式的方法
3. 化为范得蒙行列式的方法
4. 拆行(列)法
5. 降级法
6. 加边法
7. 数学归纳法
8. 递推法
9. 因式分解法
重点 行列式的计算
难点 行列式概念,行列式的展开定理及用定义证明行列式性质
3. 化为范得蒙行列式的方法
例1 计算行列式
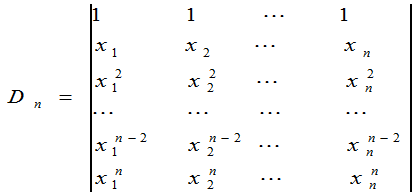
解 作如下行列式,使之配成范德蒙行列式
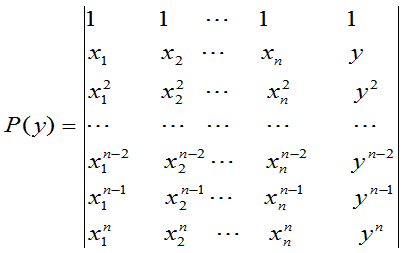 =
= 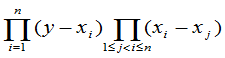
易知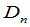 等于
等于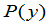 中
中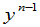 的系数的相反数,而
的系数的相反数,而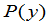 中
中 的系数为
的系数为 ,因此,
,因此,
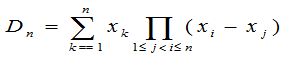 .
.
4. 拆行(列)法
例2 计算行列式
 .
.
解:
 .
.
5. 降级法
例3 计算行列式
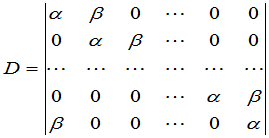 .
.
解:易得 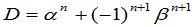 .
.
6. 加边法
例4 计算行列式
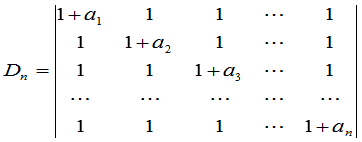 .
.
解:
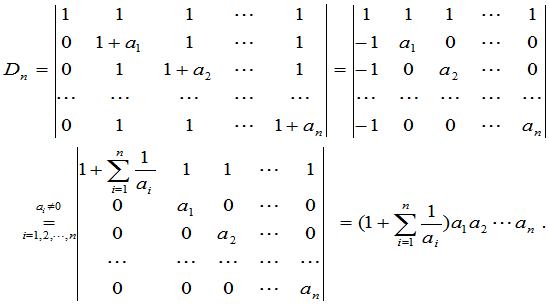
而当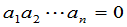 时可分只有一个因子为零或至少有两个因子为零可得同样的结果.
时可分只有一个因子为零或至少有两个因子为零可得同样的结果.
7. 数学归纳法
例5 计算行列式
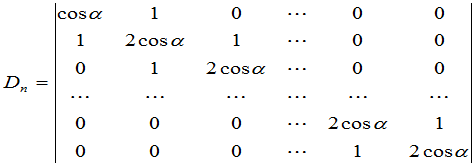 .
.
解: ,
,
于是猜想 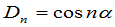 .
.
证明:对级数用第二数学归纳法证明.
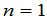 时,结论成立.假设对级数小于
时,结论成立.假设对级数小于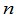 时,结论成立.将
时,结论成立.将 级行列式按第
级行列式按第 行展开,有
行展开,有
 .
.
8. 递推法:利用已给行列式的特点,建立起同类型的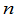 级行列式和
级行列式和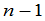 级或更低级行列式之间的关系式,称为递推公式.
级或更低级行列式之间的关系式,称为递推公式.
例6 计算行列式
 .
.
解:将行列式按第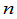 列展开,有
列展开,有
 ,
,
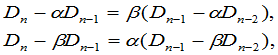
得
 。
。
同理得
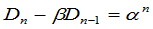 ,
,

例7 计算
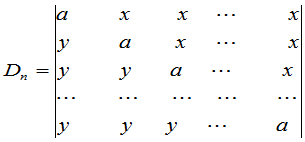
解
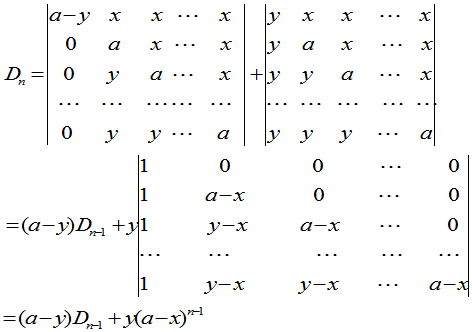
同理
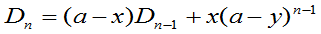
联立解得

当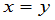 时,
时,
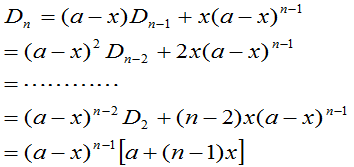
9. 因式分解法
如果行列式 是某个变数
是某个变数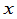 的多项式
的多项式 ,可对行列式施行某些变换,求出
,可对行列式施行某些变换,求出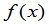 的互不相同的一次因式,设这些一次因式的乘积为
的互不相同的一次因式,设这些一次因式的乘积为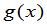 ,则
,则 ,再比较
,再比较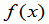 与
与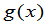 的某一项的系数,求出
的某一项的系数,求出 值.
值.
例8 计算行列式
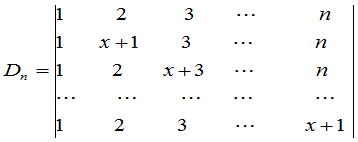 .
.
解:注意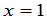 时,
时,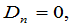 所以,
所以, .
.
同理 均为
均为 的因式
的因式
又 与
与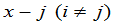 各不相同
各不相同
所以 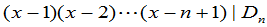
但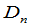 的展开式中最高次项
的展开式中最高次项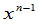 的系数为1,
的系数为1,
所以
注:此题也可将的第行减去第一行化为三角形行列式计算.




