第二章 行列式
§1 引言
解方程是代数中的一个基本的问题,特别是在中学所学代数中,解方程占有重要地位.这一章和下一章主要讨论一般的多元一次方程组,即线性方程组.
线性方程组的理论在数学中是基本的也是重要的内容.
对于二元线性方程组
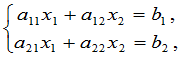
当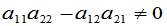 时,此方程组有唯一解,即
时,此方程组有唯一解,即
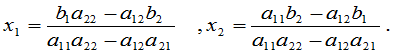
我们称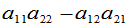 为二级行列式,用符号表示为
为二级行列式,用符号表示为
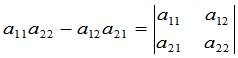 .
.
于是上述解可以用二级行列式叙述为:
当二级行列式
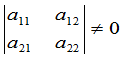
时,该方程组有唯一解,即
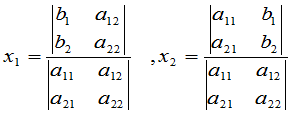 .
.
对于三元线性方程组有相仿的结论.设有三元线性方程组
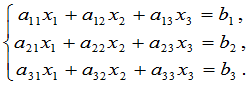
称代数式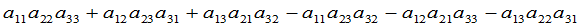 为三级行列式,用符号表示为:
为三级行列式,用符号表示为:
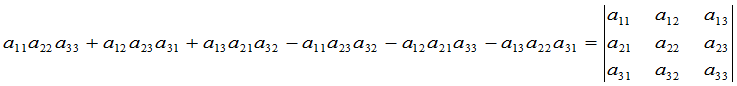 .
.
当三级行列式
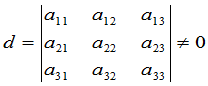
时,上述三元线性方程组有唯一解,解为
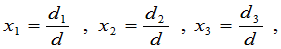
其中
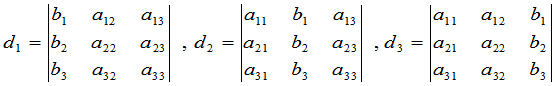 .
.
在这一章我们要把这个结果推广到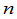 元线性方程组
元线性方程组
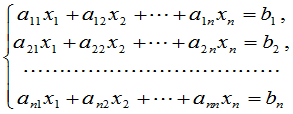
的情形.为此,首先给出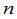 级行列式的定义并讨论它的性质,这是本章的主要内容.
级行列式的定义并讨论它的性质,这是本章的主要内容.
§2 排列
一、排列的定义
定义1 由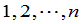 组成的一个有序数组称为一个
组成的一个有序数组称为一个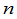 级排列.
级排列.
显然 也是一个
也是一个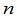 级排列,这个排列具有自然顺序,就是按递增的顺序排起来的;其它的排列或多或少地破坏自然顺序.
级排列,这个排列具有自然顺序,就是按递增的顺序排起来的;其它的排列或多或少地破坏自然顺序.
定义2 在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序,一个排列中逆序的总数就称为这个排列的逆序数.
排列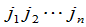 的逆序数记为
的逆序数记为
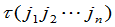
定义3 逆序数为偶数的排列称为偶排列;逆序数为奇数的排列称为奇排列.
应该指出,我们同样可以考虑由任意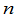 个不同的自然数所组成的排列,一般也称为
个不同的自然数所组成的排列,一般也称为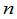 级排列.对这样一般的
级排列.对这样一般的 级排列,同样可以定义上面这些概念.
级排列,同样可以定义上面这些概念.
二、排列的奇偶性
把一个排列中某两个数的位置互换,而其余的数不动,就得到另一个排列.这样一个变换称为一个对换.显然,如果连续施行再次相同的对换,那么排列就还原了.由此得知,一个对换把全部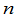 级排列两两配对,使每两个配成对的
级排列两两配对,使每两个配成对的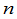 级排列在这个对换下互变.
级排列在这个对换下互变.
定理1 对换改变排列的奇偶性.
这就是说,经过一次对换,奇排列变成偶排列,偶排列变成奇排列.
推论 在全部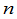 级排列排列中,奇、偶排列的个数相等,各有
级排列排列中,奇、偶排列的个数相等,各有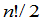 个.
个.
定理2 任意一个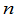 级排列与排列
级排列与排列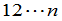 都可以经过一系列对换互变,并且所作对换的个数与这个排列有相同的奇偶性.
都可以经过一系列对换互变,并且所作对换的个数与这个排列有相同的奇偶性.
§3 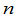 级行列式
级行列式
一、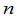 级行列式的概念
级行列式的概念
在给出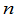 级行列式的定义之前,先来看一下二级和三级行列式的定义.我们有
级行列式的定义之前,先来看一下二级和三级行列式的定义.我们有
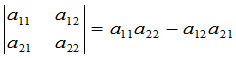 , (1)
, (1)
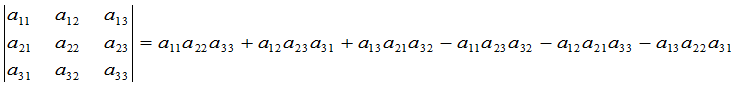 (2)
(2)
从二级和三级行列式的定义中可以看出,它们都是一些乘积的代数和,而每一项乘积都是由行列式中位于不同的行和不同的列的元素构成的,并且展开式恰恰就是由所有这种可能的乘积组成.另一方面,每一项乘积都带有符号.这符号是按什么原则决定的呢?在三级行列式的展开式(2)中,项的一般形式可以写成
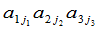 , (3)
, (3)
其中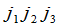 是1,2,3的一个排列.可以看出,当
是1,2,3的一个排列.可以看出,当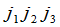 是偶排列时.对应的项在(2)中带有正号,当
是偶排列时.对应的项在(2)中带有正号,当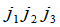 是奇排列时带有负号.
是奇排列时带有负号.
定义4
 级行列式
级行列式
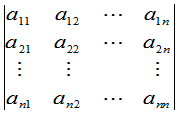 (4)
(4)
等于所有取自不同行不同列的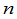 个元素的乘积
个元素的乘积
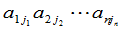 (5)
(5)
的代数和,这里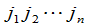 是
是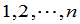 的一个排列,每一项(5)都按下面规则带有符号;当
的一个排列,每一项(5)都按下面规则带有符号;当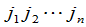 是偶排列时,(5)带有正号,当
是偶排列时,(5)带有正号,当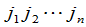 是奇排列时,(5)带有负号.这一定义可写成
是奇排列时,(5)带有负号.这一定义可写成
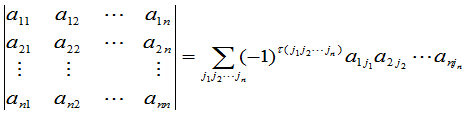 , (6)
, (6)
这里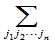 表示对所有
表示对所有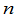 级排列求和.
级排列求和.
定义表明,为了计算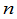 级行列式,首先作所有可能由位于不同行不同列元素构成的乘积.把构成这些乘积的元素按行指标排成自然顺序,然后由列指标所成的排列的奇偶性来决定这一项的符号.
级行列式,首先作所有可能由位于不同行不同列元素构成的乘积.把构成这些乘积的元素按行指标排成自然顺序,然后由列指标所成的排列的奇偶性来决定这一项的符号.
由定义看出,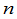 级行列式是由
级行列式是由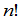 项组成的.
项组成的.
例1 计算行列式
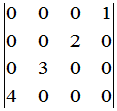 .
.
例2 计算上三角形行列式
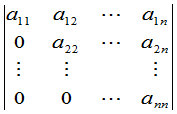 . (7)
. (7)
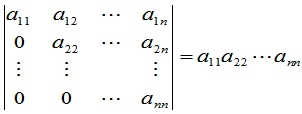 . (8)
. (8)
这个行列式就等于主对角线(从左上角到右下角这条对角线)上元素的乘积.特别主对角线以外的元素全为零的行列式称为对角形行列式.对角形行列式的值等于主对角线上元素的乘积.
容易看出,当行列式的元素全是数域中的数时,它的值也是数域中的一个数.
二、行列式的性质
在行列式的定义中,为了决定每一项的下正负号,把个元素按行指标排起来.事实上,数的乘法是交换的,因而这个元素的次序是可以任意写的,一般地,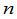 级行列式中的项可以写成
级行列式中的项可以写成
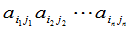 , (11)
, (11)
其中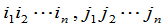 是两个
是两个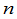 级排列.利用排列的性质,不难证明,(11)的符号等于
级排列.利用排列的性质,不难证明,(11)的符号等于
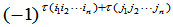 . (12)
. (12)
按(12)来决定行列式中每一项的符号的好处在于,行指标与列指标的地位是对称的,因而为了决定每一项的符号,同样可以把每一项按列指标排起来,于是定义又可以写成
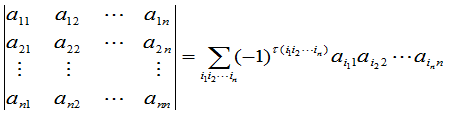 . (15)
. (15)
由此即得行列式的下列性质:
性质1 行列互换,行列式不变.即
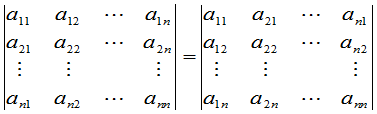 . (16)
. (16)
性质1表明,在行列式中行与列的地位是对称的,因之凡是有关行的性质,对列也同样成立. 例如由(8)即得下三角形的行列式
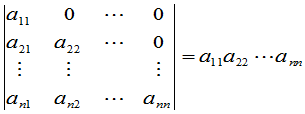 .
.
§4 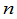 级行列式的性质
级行列式的性质
行列式的计算是一个重要的问题,也是一个很复杂的问题. 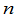 级行列式一共有
级行列式一共有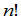 项,计算它就需做个乘法.当
项,计算它就需做个乘法.当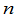 较大时,
较大时,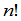 是一个相当在的数字.直接从定义来计算行列式几乎是不可能的事.因此有必要进一步讨论行列式的性质.利用这些性质可以化简行列式的计算.
是一个相当在的数字.直接从定义来计算行列式几乎是不可能的事.因此有必要进一步讨论行列式的性质.利用这些性质可以化简行列式的计算.
在行列式的定义中,虽然每一项是 个元素的乘积,但是由于这
个元素的乘积,但是由于这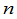 个元素是取自不同的行与列,所以对于某一确定的行中
个元素是取自不同的行与列,所以对于某一确定的行中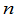 个元素(譬如
个元素(譬如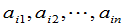 )来说,每一项都含有其中的一个且只含有其中的一个元素.因之,
)来说,每一项都含有其中的一个且只含有其中的一个元素.因之, 级行列式的
级行列式的 项可以分成
项可以分成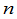 组,第一组的项都含有
组,第一组的项都含有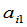 ,第二组的项都含有
,第二组的项都含有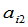 等等.再分别把
等等.再分别把 行的元素提出来,就有
行的元素提出来,就有
 (1)
(1)
其中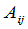 代表那些含有
代表那些含有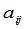 的项在提出公因子
的项在提出公因子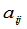 之后的代数和.至于
之后的代数和.至于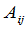 究竟是哪一些项的和暂且不管,到§6 再来讨论.从以上讨论可以知道,
究竟是哪一些项的和暂且不管,到§6 再来讨论.从以上讨论可以知道, 中不再含有第
中不再含有第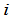 行的元素,也就是
行的元素,也就是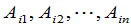 全与行列式中第
全与行列式中第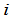 行的元素无关.由此即得.
行的元素无关.由此即得.
性质2
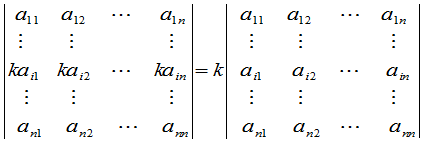
这就是说,一行的公因子可以提出去,或者说以一数乘行列式的一行相当于用这个数乘此行列式.
令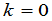 ,就有如果行列式中一行为零,那么行列式为零.
,就有如果行列式中一行为零,那么行列式为零.
性质3
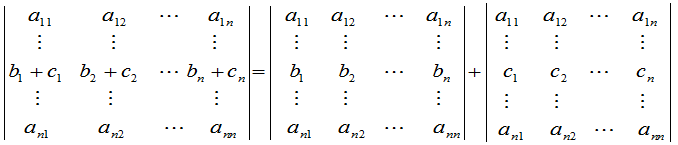 .
.
这就是说,如果某一行是两组数的和,那么这个行列式就等于两个行列式的和,而这两个行列式除这一行以外全与原来行列式的对应的行一样.
性质3显然可以推广到某一行为多组数的和的情形.
性质4 如果行列式中有两行相同,那么行列式为零.所谓两行相同就是说两行的对应元素都相等.
性质5 如果行列式中两行成比例,那么行列式为零.
性质6 把一行的倍数加到另一行,行列式不变.
性质7 对换行列式中两行的位置,行列式反号.
例1 计算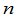 级行列式
级行列式
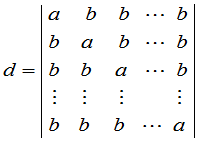
例2 计算行列式
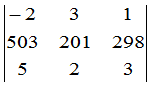 .
.
由于行列戒,上(下)三角形行列式容易计算,因此计算行列式的一个基本方法是利用行列式的性质,把行列式化成上(下)三角形行列式进行计算.
例3 一个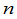 级行列式,假设它的元素满足
级行列式,假设它的元素满足
 , (4)
, (4)
证明,当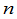 为奇数时,此行列式为零.
为奇数时,此行列式为零.
§5 行列式的计算
下面利用行列式的性质给出一个计算行列式的方法.
在§3我们看到,一个上三角形行列式
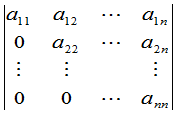
就等于它主对角线上元素的乘积
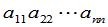
这个计算是很简单的.下面我们想办法把任意的 级行列式化为上三角形行列式来计算.
级行列式化为上三角形行列式来计算.
定义5 由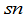 个数排成的
个数排成的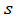 行(横的)
行(横的) 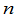 列(纵的)的表
列(纵的)的表
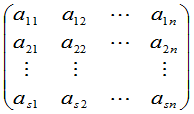 (1)
(1)
称为一个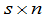 矩阵.
矩阵.
数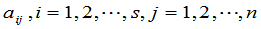 ,称为矩阵(1)的元素,
,称为矩阵(1)的元素,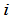 称为元素
称为元素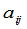 的行指标,
的行指标,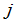 称为列指标.当一个矩阵的元素全是某一数域
称为列指标.当一个矩阵的元素全是某一数域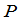 中的数时,它就称为这一数域
中的数时,它就称为这一数域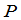 上的矩阵.
上的矩阵.
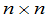 矩阵也称为
矩阵也称为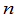 级方阵.一个
级方阵.一个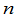 级方阵
级方阵
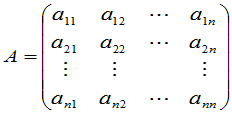
定义一个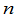 级行列式
级行列式
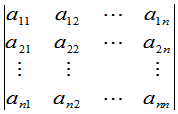
称为矩阵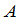 的行列式,记作
的行列式,记作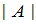 .
.
定义6 所谓数域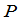 上矩阵的初等行变换是指下列三种变换:
上矩阵的初等行变换是指下列三种变换:
1)以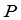 中一个非零的数乘矩阵的某一行;
中一个非零的数乘矩阵的某一行;
2)把矩阵的某一行的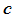 倍加到另一行,这里
倍加到另一行,这里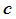 是
是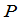 中任意一个数;
中任意一个数;
3) 互换矩阵中两行的位置.
一般说来,一个矩阵经过初等行变换后,就变成了另一个矩阵.当矩阵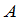 经过初等行变换变成矩阵
经过初等行变换变成矩阵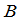 时,我们写成
时,我们写成
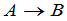
若一个矩阵的任一行从第一个元素起至该行的第一个非零元素所在的下方全为零,则称这样的矩阵为阶梯形矩阵.
可以证明,任意一个矩阵经过一系列初等行变换总能变成阶梯形矩阵.
现在回过来讨论行列式的计算问题.一个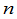 级行列式可看成是由一个
级行列式可看成是由一个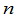 级方阵
级方阵 决定的,对于矩阵可以作初等行变换,而行列式的性质2,6,7正是说明了方阵的初等行变换对于行列式的值的影响.每个方阵
决定的,对于矩阵可以作初等行变换,而行列式的性质2,6,7正是说明了方阵的初等行变换对于行列式的值的影响.每个方阵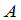 总可以经过一系列的初等行变换变成阶梯形方阵
总可以经过一系列的初等行变换变成阶梯形方阵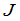 .由行列式性质2,6,7,对方阵每作一次初等行变换,相应地,行列式或者不变,或者差一非零的倍数,也就是
.由行列式性质2,6,7,对方阵每作一次初等行变换,相应地,行列式或者不变,或者差一非零的倍数,也就是

显然,阶梯形方阵的行列式都是上三角形的,因此是容易计算的.
例 计算
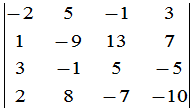
不难算出,用这个方法计算一个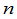 级的数字行列式只需要做
级的数字行列式只需要做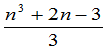 次乘法和除法.特别当
次乘法和除法.特别当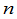 比较大的时候,这个方法的优越性就更加明显了.同时还应该看到,这个方法完全是机械的,因而可以用电子计算机按这个方法来进行行列式的计算.
比较大的时候,这个方法的优越性就更加明显了.同时还应该看到,这个方法完全是机械的,因而可以用电子计算机按这个方法来进行行列式的计算.
对于矩阵同样可以定义初等列变换,即
1)以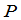 中一个非零的数乘矩阵的某一列;
中一个非零的数乘矩阵的某一列;
2)把矩阵的某一列的 倍加到另一列,这里
倍加到另一列,这里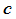 是
是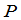 中任意一个数;
中任意一个数;
3) 互换矩阵中两列的位置.
为了计算行列式,也可以对矩阵进行初等列变换.有时候,同时用初等行变换和列变换,行列式的计算可以更简单些.
矩阵的初等行变换与初等列变换统称为初等变换.




