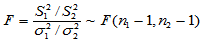1.1 总体与样本
总体：研究对象的全体。一维或多维数量指标。随机变量。
个体：每个研究对象。
样本：总体的一部分。
1.1.1简单随机样本
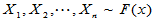，i.i.d，独立同分布。无限总体抽样。
在Matlab中各种随机数可以认为是独立同分布的，即简单随机样本。以下罗列在Matlab中的实现方法。
，均匀分布样本
n=10;x=rand(1,n)
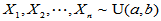
n=10;a=-1;b=3;x=rand(1,n);x=(b-a)*x+a
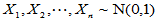，正态分布样本
n=10;x=randn(1,n)
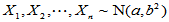
mu=80.2;sigma=7.6;m=1;n=10;
x=normrnd(mu,sigma,m,n)
上面首先对总体均值赋值mu=80.2;再对标准差赋值sigma=7.6; m=1;n=10;分别对生成的随机阵对的行数和列数进行赋值，然后可直接利用Matlab自带的函数normrnd生成正态分布的随机数。
类似地可生成m行n列的随机矩阵，服从指定的分布。生成随机数的函数后缀都是rnd，前缀为分布的名称。常用分布的随机数产生方法罗列如下，注意使用前先要对参数赋值。
x=betarnd(a,b,m,n) 参数为a,b的beta分布；
x=binornd(N,p,m,n) 参数为N,p的二项分布；
x=chi2rnd(N,m,n) 自由度为N的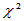
分布；
x=exprnd(mu,m,n) 总体期望为mu的指数分布；
x=frnd(n1,n2,m,n) 自由度为n1与n2的F分布；
x=gamrnd(a,b,m,n) 参数为a,b的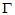
分布；
x=lognrnd(mu,sigma,m,n) 参数为mu与sigma的对数正态分布；
x=poissrnd(mu,m,n) 总体均值为mu的Poisson分布；
x=trnd(N,m,n) 自由度为N的T分布；
Matlab统计工具箱中还有一些其它分布，不再一一列举。
对于已知密度函数的不常用连续型总体，若想产生服从该分布的随机数，可用如下方法。
例1.1 设总体密度函数为
试从该总体中抽取容量为1000的简单随机样本。
解 利用matlab编辑窗口保存以下程序，保存为ex11.m
n=1000;
x=zeros(1,n);
k=0;
while k<n
a=rand*pi-pi/2;
b=rand/2;
if b<(cos(a)/2)
k=k+1;
x(k)=a;
end
end
注意理解其原理。保存完成之后，在命令窗口执行ex11，则x被赋值。再执行下列命令，就可以得到这个容量为1000的样本的直方图。
hist(x,-pi/2:0.2:pi/2)
1.1.2有限总体的无放回样本
若有限总体为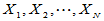
，希望从中无放回抽取容量为n的样本，这里N与n已经赋值，则可利用
r=randperm(N)
产生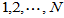
的一个随机全排列，即r是一个N维向量。于是，对于给定的N维向量X，令
x=X(r(1:n))
即可得到容量为n的无放回抽样本x。
无放回抽样中，各样本点不是独立的。
1.2 统计量
统计量：样本的函数，不含参数，可根据样本观察值立即计算出数值。
以下设
为来自总体的简单随机样本，列举出一些常用统计量。以下总假设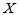
为样本，为一行
列矩阵，在Matlab中已经赋值。
1.2.1样本k阶矩
称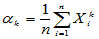
为样本k阶原点矩，对于已经赋值的正整数k,可以用如下命令得到
a(k)=mean(X.^k)
特别地，样本一阶原点矩就是样本均值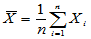
，在matlab中用mean计算。
称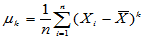
为样本k阶中心矩，对于已经赋值的正整数k,可以用如下命令得到
mu(k)=mean((X-mean(X)).^k)
特别地，称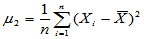
为未修正样本方差，将
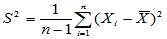
称为样本方差。称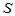
为样本标准差。Matlab中用var（X）计算样本方差，用std(X)计算样本标准差。
1.2.2顺序统计量
对于样本
，若将其依照数值大小由小到大重新排列为
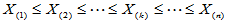
则称每个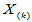
为原来样本的顺序统计量。
可以证明，若总体服从(0,1)上的均匀分布，则有
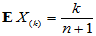
特别地，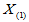
就是样本中的最小值，可用min(X)计算；
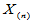就是样本中的最大值，可用max(X)计算。Matlab命令
Y=sort(X)
可立即得到X的顺序统计量，满足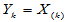
利用matlab中的sort函数，比自己编程序排序，可能会有较高效率。当在循环语句中反复使用排序时，应该优先选用。
1.2.3经验分布函数
定义1.1 设总体分布函数为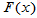
，
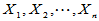为简单随机样本， 
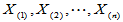为顺序统计量，记
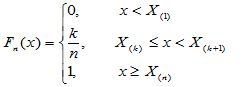（1-1）
则称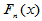
为经验分布函数或者样本分布函数。
著名的格里汶科定理指出，当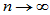
时，有
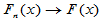a.s.
以下命令产生了来自自由度为5的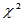
分布样本，样本容量为1000，并画出了此样本的经验分布函数。结果如图1-1所示
Y=chi2rnd(5,1,1000);[F,X]=ecdf(Y);
plot(X,F)
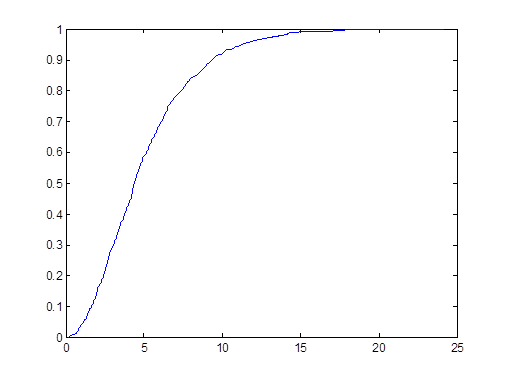
图1-1 经验分布函数示意图
以下自己编程扩展实现函数功能，将以下程序在matlab编辑窗口中输入并保存为myfn.m，今后对于myfn就可以像其它库函数一样直接调用。注意自己编写的函数文件，要注意最好可直接处理矩阵向量。以下myfn函数文件可以调试通过，但是，其编写过程还可以精确些，使得计算效率更高。如何改善请读者完成。
function y=myfn(t,x)
N=length(x); x=sort(x);
[m,n]=size(t); y=zeros(m,n);
for i=1:m
for j=1:n
s=0;
for k=1:N
if t(i,j)>=x(k)
s=s+1;
end
end
y(i,j)=s/N;
end
end
1.3 三个常用分布
以下罗列出数理统计中三个重要分布的概念与性质。
1.3.1
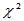分布
定义1.2 设一维连续型随机变量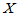
的密度函数为
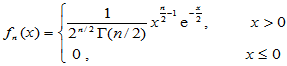（1-2）
则称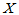
服从自由度为
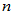的
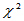分布，记为
。
图1-2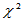 
分布密度函数示意图
（1）期望与方差：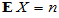
，
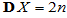
（2）来源：若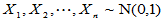
独立同分布，则
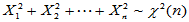
（3）可加性：若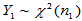
，
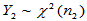，且两者独立，则有
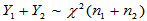
(4)重要结论：若
，则
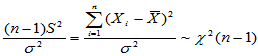
以下给出了自由度为5,10,20的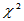
分布的密度函数，如图1-2所示。
1.3.2 t分布
定义1.3 设一维连续型随机变量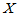
的密度函数为
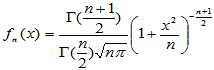（1-3）
则称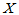
服从自由度为
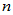的
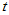分布，记为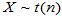
。
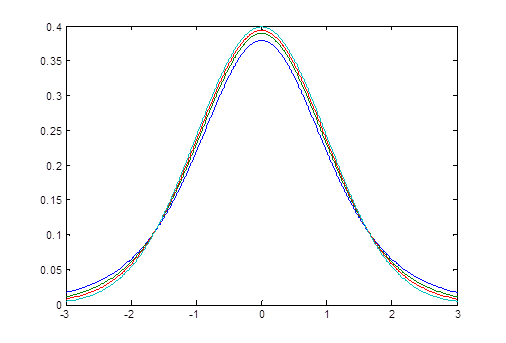
图1-3 t分布密度函数与标准正态分布密度函数
（1）密度函数特点：与标准正态分布类似，方差较大。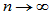
时，
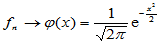（标准正态分布密度函数）
执行Matlab命令
x=-3:0.01:3; y5=tpdf(x,5);y10=tpdf(x,10);
y20=tpdf(x,20);y=normpdf(x);
plot(x,y5,x,y10,x,y20,x,y)
得到自由度为5，10，20的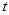
分布密度函数及标准正态分布密度函数的图形，如图1-3所示。
（2）来源：设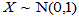
，
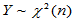，且两者独立，则
（3）重要结论：设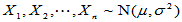
，则
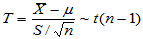
1.3.3 F分布
定义1.4 设一维连续型随机变量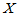
的密度函数为
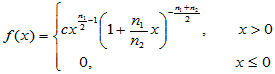（1-4）
其中常数
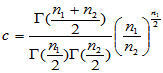
则称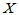
服从第一自由度
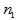，第二自由度
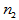的F分布，记为
。
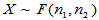（1）密度函数特点：在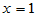
附近密度函数取值较大，为单峰非对称的。当两个自由度都很大时，
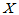取值以较大概率集中在
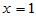附近。以下Matlab命令画出了
的密度函数。
x=0:0.01:3;y=fpdf(x,8,12);plot(x,y);
结果如图1-4所示。
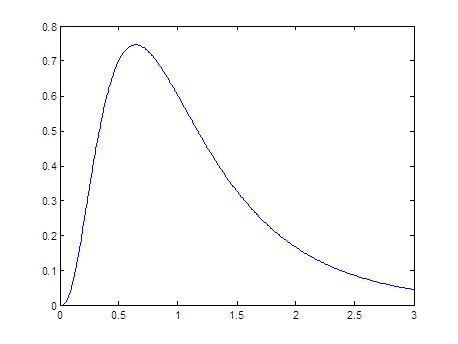
图1-4 F分布密度函数
（2）来源：设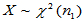
，
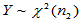，且两者独立，则
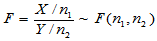
（3）重要结论：设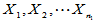
为来自总体
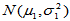的简单随机样本，
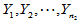为来自总体
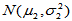的简单随机样本，且两者独立。又设两个样本方差分别为
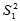与
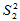，则
