本章介绍MATLAB软件的一般命令,数组操作和运算函数;绘图命令,循环和选择结构;通过实例练习解决一些简单问题.
2.1 引言
MATLAB是MATrix LABoratory的缩写,由美国MathWorks公司开发的工程计算软件,迄今已推出了7.1版.当今数学类科技应用软件可分为两类,一类是数值计算型,如MATLAB,Xmath,Gauss等,这类软件擅长数值计算,对处理大批数据效率高;另一类是数学分析型软件,如Mathematica,Maple等,这类软件以符号计算见长,能给出解析解和任意精度解,其缺点是处理大量数据时效率高.
现在, MATLAB已经发展为适合多学科,功能强大的大型软件,成为高级课程的基本教学工具.如MATLAB可以做:
微积分:微分,积分,求极限,泰勒展开,级数求和;
代数:求逆,特征值,行列式,代数方程解的简化,数学表达式的指定精度求值;
数值分析:插值与拟合,数值微分与积分,函数逼近,代数方程和微分方程的数值解和符号解.
统计计算:均值,方差,概率,参数估计,假设检验,相关性和回归分析,统计绘图,随机数产生器等.
优化问题的求解:线性规划,非线性规划等问题的求解.
动态系统模拟仿真等.
它已成为大学生,研究生和博士生必须掌握的基本技能.同时, MATLAB也被研究单位和工业部门广泛应用,使科学研究和解决各种具体问题的效率大大提高.
MATLAB集成环境主要包括五部分: MATLAB语言, MATLAB工作环境, 句柄图形,MATLAB数学函数库, MATLAB API (Application Program Interface).
MATLAB主要有以下特点:
- 运算符和库函数极其丰富,语言简洁,编程效率高. MATLAB除了提供和C语言一样的运算符外,还提供广泛的矩阵和向量运算符.
- 图形功能强大.包括对二维和三维数据可视化,图像处理,动画制作等高低层次的绘图命令.
- 功能强大的工具箱. 工具箱可分两类:功能性工具箱和学科性工具箱.前者主要用来扩充其符号计算功能,图示建模仿真,文字处理及与硬件实时交互的功能.而学科性工具箱是专业性较强的,如优化,统计,控制,小波,图像处理和通信工具箱等.
- 易于扩充.除内部函数外,所有MATLAB的核心文件和工具箱文件都是可读可改的源文件,用户可修改文件和加入自己的文件,可与库文件一样被调用.
2.1.1 安装(Windows操作平台)
- 将源光盘插入光驱;
- 在光盘的根目录下找到MATLAB的安装文件setup.exe;
- 鼠标双击该安装文件,按提示逐步完成安装;
- 安装完成后,在程序栏里便有了MATLAB选项.
2.1.2 启动
在"开始 程序
程序 Matlab
Matlab MATLAB"中单击MATLAB.便会出现MATLAB Command Window(即命令窗口).
MATLAB"中单击MATLAB.便会出现MATLAB Command Window(即命令窗口).
2.2 MATLAB环境
MATLAB既是一种语言,又是一个编程环境.
2.2.1 命令窗口






命令窗口是用户与Matlab进行交互的主要场所. Matlab语句的一般形式为:
变量=表达式
如:键入:x=4.5回车,将显示
x=
4.5
再键入:y=sin(x*pi)回车,将显示:
y
=1
';' ',' '...'的作用:
- 表达式后面跟分号';',将不显示结果;
- 跟','或不跟任何符号,将显示表达式的计算结果;
- 当一个表达式没写完就需换行时,应在该行末键入'...'之后再回车换行.如:
s=1-1/2+1/3+1/4+sin(3*x*y)-cos(x)...
-1/8+1/10+1/20
';' ',' '...'的作用:
用于命令行编辑的控制键和方向键
- 按'
 '键,会显示刚才键入的命令行;
'键,会显示刚才键入的命令行;
- 反复按'
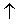 '键,可以回调以前键入的所有命令行;
'键,可以回调以前键入的所有命令行;
- '
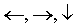 '键可以移动光标;
'键可以移动光标;
- 还有'Home','End','Esc'键等. 'Esc'清除一行.
变量
- 以字母开头,后面可跟字母,数字和下短线;
- 大小写字母有区别,不超过31个字母.
特殊变量名
ans 用于结果的缺省变量名; pi 圆周率
eps 计算机的最小数; inf 无穷大; NaN 不定量
i或j -1的开方; realmin 最小可用正实数 realmax 最大可用正实数
工作区
接受Matlab命令的内存区域,存储着命令编辑区输入的命令和创建的所有变量值.
查看或保存工作区变量:
who 或whos 显示当前工作区中的所有变量
clear 清除工作区中的所有变量
clear(变量名) 清除指定工作区的变量
save(文件名) 将当前工作区的变量储存在一个MAT-文件中
load(文件名) 调出一个MAT-文件
quit回车或单击右上角的' ',退出工作区.
',退出工作区.
2.2.2 程序编辑器
M文件:命令文件和函数文件
1. M文件的建立
1) 进入程序编辑器(MATLAB Editor/Debug):从'File'菜单中选择'New'及'M-file'项.
2) 输入程序
3) 保存程序:单击'save'按钮,出现一对话框,在文件名一框中键入一文件名,单击'保存'.
2. 命令M文件及其运行
命令M文件:一些命令行的组合,没有输入参数,也不返回输出参数.如:
% 文件名exl.m
x=4;y=6;z=2;
items=x+y+z
cost=x*25+y*22+z*99
average_cost=cost/items
- 在程序编辑窗口输入,以名为exl.m的M文件存磁盘.
- 在Matlab命令编辑窗口输入exl,便会顺序执行该文件中的命令.
3. 函数M文件及其调用
函数M文件的形式为:
fuction [输出变量列表]=函数名(输入变量列表)
函数体语句;
如:
function f=f1(x)
f=100*(x(2)-x(1)^2)^2-(1-x(1))^2;
(注意函数M文件的文件名必须与其函数名相同)
调用格式:
x=[2 3];
f=f1(x)
结果为:f=
99
2.2.3 文件管理
what 返回当前目录下的M,MAT,MEX文件的列表
dir 列出当前目录下的所有文件
cd 显示当前的工作目录
type test 在命令窗口下显示test.m的内容
delete test 删除M文件test.m
which test 显示M文件test.m所在的目
2.3 数组和函数
2.3.1 数组的运算
1) 数组的简单构造:
数组常采用':'和函数'linspace'两种输入方式,如:
x=1:5 (从1到5公差为1的等差数组)
x=0:0.1:1 (从0到1,公差为0.1)
x=linspace(0,pi,11) (11个从0到pi的等间隔数)
2) 数组的运算
设a=[a1 a2 a3],b=[b1 b2 b3],c=标量
标量加法a+b=[ a1+c a2+c a3+c]
乘法 a*c=[ a1*c a2*c a3*c]
数组加法 a+b=[ a1+ b1 a2+ b2 a3+ b3]
乘法 a.*b= [a1*b1 a2*b2 a3*b3]
数组右除 a./b= [a1/b1 a2/b2 a3/b3]
左除 a.\b= [b1 /a1 b2/ a2 b3/ a3]
数组求幂 a.^c=[ a1^c a2^c a3^c]
c. ^a=[ a1^c a2^c a3^c]
a.^b= [a1^b1 a2^b2 a3^b3] sort(v) 按升序排列
max(v) 求最大值 min(v) 求最小值 sum(v) 求和 mean(v) 求平均
2.3.2 矩阵的创建
1) 矩阵的直接定义 键入: A=[1 2 3;4 5 6]
或键入:A=[1 2 3
4 5 6 ]
2) 特殊矩阵
zeros(m,n) ones(m,n) eye(n) rand(m,n) diag(v) triu(x)
3) 矩阵的剪裁和拼接
键入:A=[1 2 3 ;4 5 6; 7 8 9];A(3.:) %A的第三行
输出:ans= 7 8 9
键入:B=A(2:3,:) %A的第二,三行
输出:B=
4 5 6
7 8 9
键入:A(:,1) %A的第一列
输出:ans=
1
4
7
输入: C=[B,zeros(2,1)]
输出: C=
4 5 6 0
7 8 9 0
2.3.3 矩阵的运算
+ 矩阵加法 – 矩阵减法 * 乘法 , 转置 ^ 乘幂 / 左除 \ 右除
如:A是可逆矩阵,AX=B的解是A左除B,即X=A\B; XA=B的解X= B/A. rank(A) 矩阵秩 inv(A) 矩阵的逆 det(A) 行列式 orth(A) 正交化 poly(A) 特征多项式
2.3.4 数学函数
sin(x) cos(x) tan(x) cot(x) exp(x) log(x) log10(x) sqrt(x) 平方根
朝零方向取整 fix(x) 朝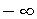 方向取整floor(x) 朝
方向取整floor(x) 朝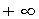 方向取整 ceil(x) 四舍五入到最近的整数round(x) 符号函数sign(x)
方向取整 ceil(x) 四舍五入到最近的整数round(x) 符号函数sign(x)
2.4 图形功能
2.4.1 二维图形
1) 基本绘图命令
plot(x, y, 'color-linestyle-marker')
x, y------转折点; color-linestyle-marker-------连线颜色,线型,数据点图标.
颜色:y黄 r红 g绿 b 蓝 w 白 k 黑 m紫 c 灰 -实线 :点线 --虚线
数据点图标: . 小黑点 +加法 *星号 O小圆圈 pentagram 五角星
x=1:8;y=sin(x);plot(x,y,'k : O')
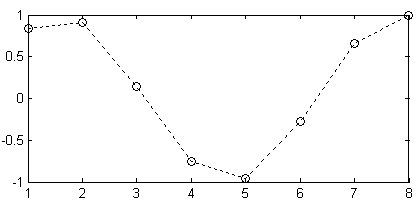
plot(x,y,' O')
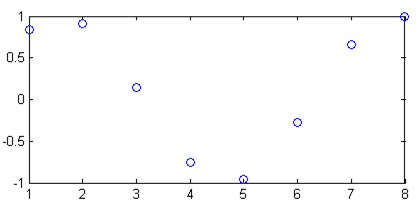
x=0:0.1:2*pi; y=sin(x); plot(x,y, 'r:o');
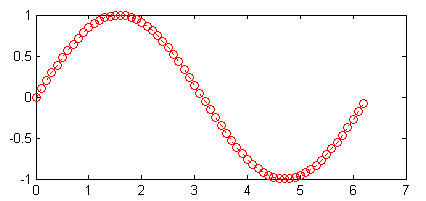
plot(x,y, 'r :');
2) 坐标系的控制
axis([xmin xmax ymin ymax]) [ ]中分别给出X轴和Y轴的最小,最大值;
axis equal X轴和Y轴的单位长度相同. axis squrare 图框呈方形 axis off 取消坐标轴
3) 图形标注
x=linspace(0,2*pi,30);y=[sin(x);cos(x)];plot(x,y);
grid;xlabel('x');ylabel('y');title('sine and cosine curves');
text(3*pi/4,sin(3*pi/4),'\leftarrowsinx'); text(3*pi/2,cos(3*pi/2),'cosx\rightarrow',...
'HorizontalAlignment','right');
(以上命令行可以形成一个M文件).hold on 把新的图形画在原来图形上.
grid 在图形上加网格 xlabel ylabel 对X,Y轴加注 title 给整个图形加标题
text gtext 在图形中特定位置加字符串.若使用gtext('sinx')代替命令text,则在图形窗口会出现十字线,其交点是字符串位置.移动鼠标可移动交点,点击鼠标即可将字符串固定.输出结果如下图:
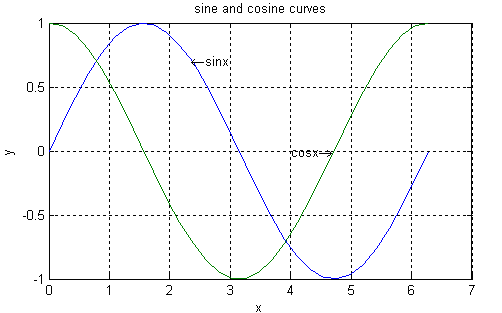
4) 多幅图形
在同一画面中的多幅不同坐标系的图形,如何作?
x=linspace(0,2*pi,30);y=sin(x);z=cos(x);u=2*sin(x).*cos(x);v=sin(x)./cos(x);subplot(2,2,1),plot (x,y),title('sin(x)'); subplot(2,2,2),plot (x,z),title('cos(x)');
subplot(2,2,3),plot (x,u),title('2sin(x)cos(x)'); subplot(2,2,4),plot (x,v),title('sin(x)/cos(x)');
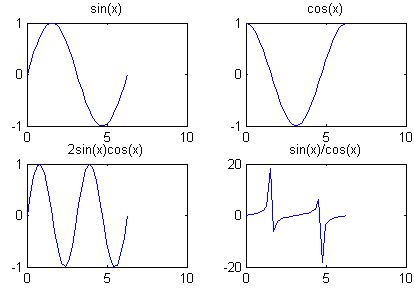
2.4.2 三维图形
1) 空间曲线
例:作螺旋线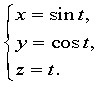 键入: t=0:pi/51:10*pi;plot3(sin(t),cos(t),t);
键入: t=0:pi/51:10*pi;plot3(sin(t),cos(t),t);

2) 带网格的曲面
作曲面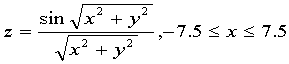 .键入:
.键入:
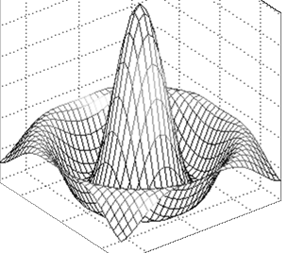
x=-7.5:0.5:7.5;y=x;
[X,Y]=meshgrid(x,y); % 三维图形的X,Y数组
R=sqrt(X.^2+Y.^2)+eps; % +eps是为防止出现0/0
Z=sin(R)./R;mesh(X,Y,Z); % 三维网格表面
3) 等高线
4) 条形图和面积图: 某产品上半年的销售利润profit,每月份售出产品的产值expense.
x=1:1:6;
expense=[ 21 34 89 25 22 90];profit=[ 10 20 60 11 9 70]
sale=[ expense; profit]; area(x,sale)
2.5 M文件的编写
2.5.1 M文件
1) 命令M文件:一些命令行的组合. 函数M文件:定义函数的程序,具有一定的特定格式;
如: 命令M文件:x=[2 3];f=cos(x)
函数M文件:function f=cost(x)
f=100*(x(2)-x(1)^2)^2…
-(1-x(1))^2;
2) 函数M文件的形式为:
function [输出变量列表]=函数名(输入变量列表)
函数体语句:
2.5.2 四种循环和选择控制结构
1) while
关系表达式 { statements }
end
s=0;n=1
while s<=100
s=s+n^2;n=n+1;
end
n,s
2) for
for x=x1:step:xn
{ statements }
end
如: for k=1:4
x(k)=1/k;
end
format rat %设置输出格式为有理数
x
例:建立一个函数M文件求自然数n的阶乘.
function f=jch(n)
f=1;
for i=1:n
f=f*I;
end
3) switch 表达式(标量或字符串)
case 值1,
语句体1
case {值2.1,值2.2,…}
语句体2
…
otherwise,
语句体n
end
for x=x1:step:xn
{ statements }
end




