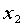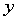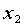- 矩阵的生成
1)直接输入 2)函数生成 3)文本文件
- 简单数组
MATLAB的运算事实上是以数组 (array) 及矩阵 (matrix) 方式在做运算,而这二者在MATLAB的基本运算性质不同,数组强调元素对元素的运算,而矩阵则采用线性代数的运算方式。
宣告一变数为数组或是矩阵时,如果是要个别键入元素,须用中括号[ ] 将元素置于其中。数组为一维元素所构成,而矩阵为多维元素所组成,例如
» x=[1 2 3 4 5 6 7 8] ; %一维 1x8 数组
» x = [1 2 3 4 5 6 7 8; 4 5 6 7 8 9 10 11] ;
% 二维 2x8 矩阵,以";"或回车分隔各行的元素,以","或空格分隔各列的元素
» x = [1 2 3 4 5 6 7 8 % 二维 2x8 矩阵,各列的元素分二行键入
4 5 6 7 8 9 10 11] ;
» x(3) % x的第三个元素
» x([1 2 5]) % x的第一、二、五个元素
» x(1:5) % x的第前五个元素
ans = 1 4 2 5 3
» x(10:end) % x的第十个元素后的元素
ans = 8 6 9 7 10 8 11
» x(10:-1:2) % x的第十个元素和第二个元素的倒排
ans = 8 5 7 4 6 3 5 2 4
» x(find(x>5)) % x中大于5的元素
» x(4)=100 %给x的第四个元素重新给值
» x(3)=[] % 删除第三个元素
» x(16)=1 % 加入第十六个元素
- 建立数组(向量)
上面的方法只适用于元素不多的情况,但是当元素很多的时候,则须采用以下的方式:
» x=(0:0.02:1); % 以:起始值=0、增量值=0.02、终止值=1的矩阵(用":"生成)
» x=linspace(0,1,100);
% 利用linspace,以区隔起始值=0终止值=1之间的元素数目=100(线性等分向量)
»a=[] %空矩阵
» zeros(2,2) %全为0的矩阵
» ones(3,3) %全为1的矩阵
» rand(2,4); % 随机矩阵
»a=1:7, b=1:0.2:5; %更直接的方式
»c=[b a]; %可利用先前建立的数组 a 及数组 b ,组成新数组
» a=1:1:10;
» b=0.1:0.1:1;
» a+b*I %复数数组
- 子矩阵
通过一个矩阵产生另一个矩阵的方法(上面已经有例子)
假如一个矩阵A
则 A(m1:m2 ,n1:n2)
- 矩阵的运算
- 经典的算术运算符。
运算符 MATLAB表达式
加 | + | a+b |
减 | - | a-b |
乘 | * | a*b |
除 | / 或 \ | a/b或a\b |
幂 | ^ | a^b |
» a=1:1:10;
» b=0:10:90;
» a+b
» a.*b %注意这里a后加了个".",表示数组相乘, 是元素对元素的乘积
» a*b %表示矩阵相乘, 要求矩阵a的列数与矩阵b的行数一致
» a/b %矩阵右除 inv(a)*b
» a\b %矩阵左除 a*inv(b)
» a./b %数组右除,数组中对应元素相除, a(i,j)/b(i,j)
» a.\b %数组左除,数组中对应元素相除 b(i,j)/a(i,j)
» a^b %矩阵乘方,涉及到特征值和特征向量的求解。
» a.^b %数组乘方,a和b中对应元素的乘方,即a(i,j)的b(i,j)次方。
说明:在这里特别要注意一下有没有加点"."之间的区别,这些算术运算符所运算的两个阵列是否需要长度一致。
- 矩阵转置运算
通过在矩阵变量后加' 的方法来表示转置运算
» a=1:1:10;
» b=0:10:90;
» a'
» c=a+b*i;
» c'
- 矩阵函数
- MATLAB常用数学函数
基本数学函数一般都可以作为矩阵函数。如三角函数、指数对数函数等。
» a=1:1:10;
» b=0:10:90;
» sin(a)
» exp(b)
» sign(a)
» mean(b)
- 求矩阵的长度的函数
» A=[10, 2, 12; 34, 2, 4; 98, 34, 6];
» size(A) % 矩阵A的行列大小 3*3
» length(A) % 返回size(A) 中的最大值
- 矩阵的几种基本变换操作
1) 通过在矩阵变量后加'的方法来表示转置运算
» A=[10,2,12;34,2,4;98,34,6];
» A'
2) 矩阵求逆 inv(A): 返回矩阵a的逆阵。
» A=[1 2 3; 4 5 6; 7 8 9];
» inv(A)
3) 矩阵求伪逆pinv(A):
» A=[1 2 3; 4 5 6; 7 8 0; 2 5 8]; %3个未知量的4个方程
» pinv(A)
4) 矩阵翻转:
左右反转:矩阵关于垂直轴沿左右方向进行列维翻转
fliplr(A)
» A=[1 4; 2 5; 3 6];
» fliplr(A)
上下反转:矩阵关于水平轴沿上下左右方向进行列维翻转
flipud(A)
» A=[1 4; 2 5; 3 6];
» flipud(A)
5) 旋转90度
rot90(A)
例: » A=[1 4; 2 5; 3 6];
» rot90(A)
6) 矩阵的特征值
[U,V]=eig(A): 返回方阵A所有特征值组成的矩阵U和特征向量组成的矩阵V
例: » A=[6 12 19; -9 –20 –33; 4 9 15];
» [U,V]=eig(A)
7) 取出上三角和下三角
triu(A) : 取上三角阵
tril(A) :取下三角阵
[L,U]=lu(A):作LU分解(Gauss消去法),L为主对角线元素都为1的上三角矩阵,U为一个下三角矩阵
例:» A=[1 5 2; 3 4 6; 5 3 2];
» triu(A)
» tril(A)
» [L,U]=lu(A)
8) 正交分解:QR分解,Q为正交矩阵,R为上三角矩阵
[Q,R]=qr(A)
例: » A=[1 2; 5 7; 7 3; 9 1];
» [Q,R]=qr(A)
9) 奇异值分解: [U,S,V]=svd(A),矩阵U和V是正交矩阵,S为A的奇异值矩阵。
例: » A=[9 4; 6 8; 2 7];
» [U,S,V]=svd(A)
10) 求矩阵的范数
norm(A,1) 计算矩阵A的1范数
norm(A,2) 计算矩阵A的2范数
norm(A,inf) 计算矩阵A的无穷范数
例:» A=rand(3);
» norm(A,1)
» norm(A,2)
» norm(A,inf)
11) 求矩阵的行列式的值 det(A)
例: » A=[1 2 3; 4 5 6; 7 8 9]
» det(A)
- 基本二维绘图命令
MATLAB不但擅长于矩阵相关的数值运算,也适合用在各种科学可视化(Scientific visualization)。下面介绍MATLAB基本二维和三维的各项绘图命令,包含一维曲线及二维曲面的绘制、打印及保存。
- plot是绘制一维曲线的基本函数,但在使用此函数之前,我们需先定义曲线上每一点的x及y坐标。下例可画出一条正弦曲线:
» x=linspace(0, 2*pi, 100); % 100个点的x坐标
» y=sin(x); % 对应的y坐标
» plot(x,y);
- 若要画出多条曲线,只需将坐标对依次放入plot函数即可:
» plot(x, sin(x), x, cos(x));
- 若要改变颜色,在坐标对后面加上相关字符串即可:
» plot(x, sin(x), 'c', x, cos(x), 'g');
- 若要同时改变颜色及线型(Line style),也是在坐标对后面加上相关字符串即可:
» plot(x, sin(x), 'co', x, cos(x), 'g*');
plot绘图函数的参数
字符 | 颜色 | 字符 | 图线型态 |
黄色 | . | 点 | |
k | 黑色 | o | 圆 |
w | 白色 | x | x |
b | 蓝色 | + | + |
g | 绿色 | * | * |
r | 红色 | - | 实线 |
c | 亮青色 | : | 点线 |
m | 锰紫色 | -. | 点虚线 |
-- | 虚线 |
- 图形完成后,我们可用axis([xmin,xmax,ymin,ymax])函数来调整坐标轴的范围:
» axis([0, 6, -1.2, 1.2]);
- MATLAB也可对图形加上各种注解与处理:
» xlabel('Input Value'); % x轴注解
» ylabel('Function Value'); % y轴注解
» title('Two Trigonometric Functions'); % 图形标题
» legend('y = sin(x)','y = cos(x)'); % 图形注解
» grid on; % 显示格线
- 用subplot来同时画出数个小图形于同一个窗口之中:
» subplot(2,2,1); plot(x, sin(x)); %把窗口分成2*2个子窗口,在第一个子窗口绘图
» subplot(2,2,2); plot(x, cos(x)); %在第二个子窗口绘图
» subplot(2,2,3); plot(x, sinh(x)); %在第三个子窗口绘图
» subplot(2,2,4); plot(x, cosh(x)); %在第四个子窗口绘图
- MATLAB还有其他各种二维绘图函数,以适合不同的应用,详见下表。
Bar | 长条图 |
Errorbar | 图形加上误差范围 |
Fplot | 较精确的函数图形 |
Polar | 极坐标图 |
Hist | 累计图 |
Rose | 极坐标累计图 |
Stairs | 阶梯图 |
Stem | 针状图 |
Fill | 实心图 |
Feather | 羽毛图 |
Compass | 罗盘图 |
Quiver | 向量场图 |
以下我们针对每个函数举例。
- 当数据点数量不多时,条形图是很适合的表示方式:
» close all; % 关闭所有的图形窗口
» x=1:10;
» y=rand(size(x));
» bar(x,y);
- 如果已知数据的误差量,就可用errorbar来表示。下例以单位标准差来做数据的误差量:
» x = linspace(0,2*pi,30);
» y = sin(x);
» e = std(y)*ones(size(x));
» errorbar(x,y,e)
- 对于变化剧烈的函数,可用fplot来进行较精确的绘图,会对剧烈变化处进行较密集的取样,如下例:
» fplot('sin(1/x)', [0.02 0.2]); % [0.02 0.2]是绘图范围
- 若要产生极坐标图形,可用polar:
» theta=linspace(0, 2*pi);
» r=cos(4*theta);
» polar(theta, r);
- 对于大量的数据,我们可用hist来显示数据的分布情况和统计特性。下面几个命令可用来验证randn产生的高斯随随机数分布:
» x=randn(5000, 1); % 产生5000个 m=0,s=1 的高斯随机数
» hist(x,20); % 20代表长条的个数
- rose和hist很接近,只不过是将数据大小视为角度,数据个数视为距离,并用极坐标绘制表示:
» x=randn(1000, 1);
» rose(x);
- stairs可画出阶梯图:
» x=linspace(0,10,50);
» y= sin(x).*exp(-x/3);
» stairs(x,y);
- stems可产生针状图,常被用来绘制数位讯号:
» x=linspace(0,10,50);
» y=sin(x).*exp(-x/3);
» stems(x,y);
- fill将数据点视为多边行顶点,并将此多边行涂上颜色:
» x=linspace(0,10,50);
» y=sin(x).*exp(-x/3);
» fill(x,y,'b'); % 'b'为蓝色
- feather将每一个数据点视复数,并以箭号画出:
» theta=linspace(0, 2*pi, 20);
» z = cos(theta)+i*sin(theta);
» feather(z);
- compass和feather很接近,只是每个箭号的起点都在圆点:
» theta=linspace(0, 2*pi, 20);
» z = cos(theta)+i*sin(theta);
» compass(z);
- 基本三维绘图命令
在科学可视化(Scientific visualization)中,三维空间的立体图是一个非常重要的技巧。下面介绍MATLAB基本三维空间的各项绘图命令。
- mesh和plot是三度空间立体绘图的基本命令,mesh可画出立体网状图,surf则可画出立体曲面图,两者产生的图形都会依高度而有不同颜色。下列命令可画出由函数形成的立体网状图:
» x=linspace(-2, 2, 25); % 在x轴上取25点
» y=linspace(-2, 2, 25); % 在y轴上取25点
» [xx,yy]=meshgrid(x, y); % xx和yy都是21x21的矩阵
» zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是21x21的矩阵
» mesh(xx, yy, zz); % 画出立体网状图
- surf和mesh的用法类似:
» x=linspace(-2, 2, 25); % 在x轴上取25点
» y=linspace(-2, 2, 25); % 在y轴上取25点
» [xx,yy]=meshgrid(x, y); % xx和yy都是21x21的矩阵
» zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是21x21的矩阵
» surf(xx, yy, zz); % 画出立体曲面图
- meshc同时画出网状图与等高线:
» [x,y,z]=peaks;
» meshc(x,y,z);
» axis([-inf inf -inf inf -inf inf]);
- surfc同时画出曲面图与等高线:
» [x,y,z]=peaks;
» surfc(x,y,z);
» axis([-inf inf -inf inf -inf inf]);
- contour3画出曲面在三维空间中的等高线:
» contour3(peaks, 20);
» axis([-inf inf -inf inf -inf inf]);
- contour画出曲面等高线在XY平面的投影:
» contour(peaks, 20);
- plot3可画出三维空间中的曲线, 也可同时画出两条三维空间中的曲线
» t=linspace(0,20*pi, 501);
» plot3(t.*sin(t), t.*cos(t), t);
» t=linspace(0, 10*pi, 501);
» plot3(t.*sin(t), t.*cos(t), t, t.*sin(t), t.*cos(t), -t);
3.6 语句、变量和表达式
- 语句形式 变量=表达式
输入一个语句并以回车结束,则在工作区显示计算结果,语句以";"结束,只进行计算但不显示结果。太长的表达式可以用续行号…将其延续到下一行。一行可以写几个语句,它们之间用逗号或句号分开。
- 变量 由字母、数字和下划线组成,最多31个字符,区分大小写字母,第一个字符必须是字母。不需要类型说明和维数语句。
- 几个特殊的量 pi 圆周率⑷π;eps 最小浮点数;Inf 正无穷大;NaN 不定值
I,j 虚数单位
- 字符串 用单引号括起来的字符集
3.7 函数
- 标量函数 sin cos tan cot sec csc asin acos sinh cosh sqrt exp log
log10 abs floor ceil fix sign real imag angle rats
- 向量函数 max min sum length mean median prod(乘积)sort(从小到大排列)
例 a=[4,3.1,-1.2,0.6];b=min(a),c=sum(a),e=sort(a)
3.8 程序设计
- Matlab有两种工作方式:1)人机交互的命令行指令操作方式,2)进行控制流的程序设计,即编制一种可存储的以M为扩展名的文件(简称M文件),在Matlab下执行该程序
- 命令式M文件: 就是将Matlab的命令按顺序编制成一个文本文件
- 函数式M文件: 主要用来定义函数子程序,它由function起头,后跟的函数名必须与文件名相同,它有输入输出元(变量),可进行变量传递。
例 计算第n个Fibonnaci数的函数文件fibfun.m
function f=fibfun(n)
if n>2
f=fibfun(n-1)+fibfun(n-2);
else f=1;
end
3.9 控制语句
- 循环语句
for循环:for v=s1:s2:s3 %(s1-循环变量初值,s2-循环变量增量,s3-循环变量终值
执行语句
end
例 求1+2+…+100(sum100.m)
mysum=0;
for i=1:1:100
mysum=mysum+i;
end
mysum
while循环:while 逻辑变量
循环体语句
end
例 求1+2+…+100(sum100w.m)
mysum=0;
i=1;
while (i<=100)
mysum=mysum+i;
i=i+1;
end
mysum
- 选择语句
if 逻辑变量
条件语句组
end
if 逻辑变量
条件语句组1
else
条件语句组2
end
if逻辑变量1
条件语句组1
elseif逻辑变量2
条件语句组2
…
elseif逻辑变量n
条件语句组n
else
条件语句组n+1
end
例 符号函数(fhfun.m)

function f=fhfun(x)
if x>0
f=1;
elseif x==0
f=0;
else
f=-1;
end
f
3.10 人机交互语句
- 输入语句input:A=input(提示字符串), A=input(提示字符串,'s')
- 键盘输入命令:keyboard
- 中断命令:break
例 鸡兔同笼,头36,脚100,鸡兔各几?(jt.m)
i=1;
while 1
if (i+(100-i*2)/4)==36
break
end
i=i+1;
end
a1=i
a2=36-i
3.11 在科学计算中的应用
- 数值微分
diff(x)-x=[x1,x2,…,xn],diff(x)=[x2-x1,…,xn-xn-1]
y'=dy/dt=diff(y)/dt—dt=xi+1-xi
- 数值积分
Simpson法求积:quad(f,a,b,tol)
Newton-cots求积:quad8(f,a,b,tol)
梯形公式求积:trapz(x,y)
例 卫星轨道长度
 ,a=6371+2384,b=6731+439
,a=6371+2384,b=6731+439
wxfun.m
function y=wxfun(t)
a=8755;b=6810;
y=sqrt(a^2*sin(t).^2+b^2*cos(t).^2);
t=0:pi/10:pi/2;y1=wxfun(t);l1=4*trapz(t,y1)
l2=4*quad(@wxfun,0,pi/2,1e-6)
- 多重定积分的数值求解
求双重定积分问题
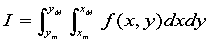
的Matlab函数为
y=dblquad('fun',x_m,x_M,y_m,y_M,tol)
例 求
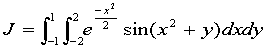
function z=mydbl(x,y)
z=exp(-x.^2/2).*sin(x.^2+y);
y=dblquad('mydbl',-2,2,-1,1)
y =
1.5746
- 常微分方程数值解法
求解微分方程初值问题

在区间[t0,tf]的数值解的函数为
[t,x]=ode23('fun',[t0,tf],x0,'选项')----2/3阶RKF(Runge-Kutta-Felhberg)法
[t,x]=ode45('fun',[t0,tf],x0,'选项')----4/5阶RKF(Runge-Kutta-Felhberg)法
其中函数fun的编写格式如下:
function xdot=fun(t,x)
例 考虑著名的Van der Pol方程

令 则原方程变化为
则原方程变化为

function y=vdp_eq(t,x,flag,mu)
y=[x(2);-mu*(x(1).^2-1).*x(2)-x(1)];
vdpl.m
h_opt=odeset;x0=[-0.2;-0.7];t_f=20;
mu=1;[t1,y1]=ode45('vdp_eq',[0,t_f],x0,h_opt,mu);
mu=2;[t2,y2]=ode45('vdp_eq',[0,t_f],x0,h_opt,mu);
plot(y1(:,1),y1(:,2),y2(:,1),y2(:,2))
例 食饵-捕食者模型
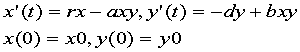
其中x(t),y(t)分别表示食饵和捕食者t时刻的数量. 求r=1,d=0.5,a=0.1,b=0.02,x0=25,y0=2时的数值解,并画出x(t),y(t)的图形以及相图(x,y).
function xdot=shier(t,x)
r=1;d=0.5;a=0.1;b=0.02;
xdot=diag([r-a*x(2),-d+b*x(1)])*x;
s_b.m
ts=0:0.1:15;x0=[25,2];
[t,x]=ode45('shier',ts,x0);
[t,x],
plot(t,x),grid,gtext('x1(t)'),gtext('x2(t)'),
plot(x(:,1),x(:,2)),grid,xlabel('x1'),ylabel('x2')
3.12 优化计算
- 线性规划
linprog
求
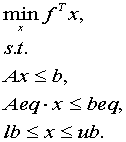
linprog(f,A,B,Aeq,Beq,lb,ub)
linprog(f,A,B,Aeq,Beq,lb,ub,x0) linprog(f,A,B,Aeq,Beq,lb,ub,x0,options)
例1 求解线性规划问题

s.t. 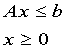
其中c=[-0.4,-0.28,-0.32,-0.72,-0.64,-0.6]
A=[0.01 0.01 0.01 0.03 0.03 0.03
0.02 0 0 0.05 0 0
0 0.02 0 0 0.05 0
0 0 0.03 0 0 0.08]
b=[850;700;100;900]
vlb=[0;0;0;0;0;0]
vub=[]
- 无约束优化
fminunc
Find a minimum of an unconstrained multivariable function
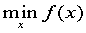
where x is a vector and f(x) is a function that returns a scalar. Syntaxx = fminunc(fun,x0)
x = fminunc(fun,x0,options)
x = fminunc(fun,x0,options,P1,P2,...)
[x,fval] = fminunc(...)
[x,fval,exitflag] = fminunc(...)
[x,fval,exitflag,output] = fminunc(...)
[x,fval,exitflag,output,grad] = fminunc(...)
[x,fval,exitflag,output,grad,hessian] = fminunc(...)
例 求
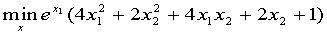
----
function f = objfun(x)
f = exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
unop.m
x0 = [1,1];
[x,fval] = fminunc(@myfun,x0)
- fmincon
Find a minimum of a constrained nonlinear multivariable function
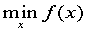
subject to

where x, b, beq, lb, and ub are vectors, A and Aeq are matrices, c(x) and ceq(x) are functions that return vectors, and f(x) is a function that returns a scalar. f(x), c(x), and ceq(x) can be nonlinear functions. Syntaxx = fmincon(fun,x0,A,b)
x = fmincon(fun,x0,A,b,Aeq,beq)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options,P1,P2, ...)
[x,fval] = fmincon(...)
[x,fval,exitflag] = fmincon(...)
[x,fval,exitflag,output] = fmincon(...)
[x,fval,exitflag,output,lambda] = fmincon(...)
[x,fval,exitflag,output,lambda,grad] = fmincon(...)
[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(...)
例 求
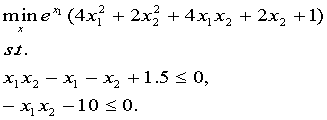
function f = objfun(x)
f = exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
function [c, ceq] = confun(x)
% Nonlinear inequality constraints
c = [1.5 + x(1)*x(2) - x(1) - x(2);
-x(1)*x(2) - 10];
% Nonlinear equality constraints
ceq = [];
cop.m
x0 = [-1,1]; % Make a starting guess at the solution
options = optimset('LargeScale','off');
[x, fval] = ...
fmincon(@objfun,x0,[],[],[],[],[],[],@confun,options)
3.13 曲线拟合
已知一组数据(二维),即平面上的 个点
个点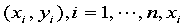 互不相同,寻求一个函数
互不相同,寻求一个函数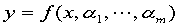 ,使其在某种准则下与所有数据点最为接近。
,使其在某种准则下与所有数据点最为接近。
- 线性最小二乘法
令

其中 是事先选定的一组函数,
是事先选定的一组函数,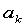 是待定系数。拟合准则是使
是待定系数。拟合准则是使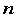 个点
个点 与
与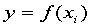 的距离的平方和最小(称为最小二乘准则),即求使
的距离的平方和最小(称为最小二乘准则),即求使
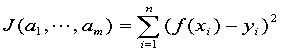
达到最小的 .令
.令 ,可得出
,可得出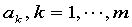 ,满足的线性方程组
,满足的线性方程组
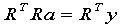
其中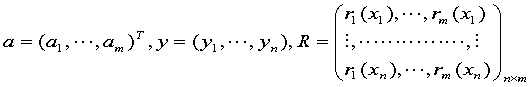
关键的一步是选取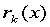 ,可根据机理分析或
,可根据机理分析或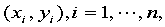 的图形判断。
的图形判断。
取 ,为多项式拟合,Matlab命令为
,为多项式拟合,Matlab命令为
a=polyfit(x,y,m)
其中输入参数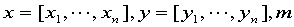 为拟合多项式的次数,输出参数
为拟合多项式的次数,输出参数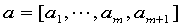 为拟合多项式
为拟合多项式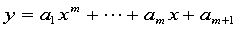 的系数。
的系数。
拟合多项式在 处的值可用Matlab命令y=polyval(a,x)计算
处的值可用Matlab命令y=polyval(a,x)计算
例 电阻问题 已知一对温度敏感的电阻的阻值和温度的一组数据如下
t(度) 20.5,32.7,51.0,73.0,95.7
R(欧姆) 765, 826, 873, 942,1032
拟合电阻 与温度
与温度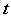 之间的关系
之间的关系
Matlab命令(dianzu.m)如下
t=[20.5,32.7,51.0,73.0,95.7];
r=[ 765,826,873,942,1032];
aa=polyfit(t,r,1);
a=aa(1)
b=aa(2)
y=polyval(aa,t);
plot(t,r,'k+',t,y,'r')
例 血药浓度问题 某人用快速静脉注射方式一次注入药物300mg,在一定时刻采集血样,测得血药浓度如下:
t=0.25,0.5,1,1.5,2,3,4,6,8
c=19.21,18.15,15.36,14.10,12.89,9.32,7.45,5.24,3.01
拟合血药浓度随时间的变化规律。
利用机理分析(一室模型)可得
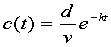
为拟合系数 ,我们对上式取对数得
,我们对上式取对数得
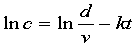
记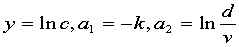 ,则问题化为由数据
,则问题化为由数据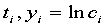 拟合直线
拟合直线
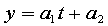
用如下Matlab命令(xueyao.m)
t=[0.25,0.5,1,1.5,2,3,4,6,8];
c=[ 19.21,18.15,15.36,14.10,12.89,9.32,7.45,5.24,3.01];
y=log(c);
aa=polyfit(t,y,1);
a=aa(1)
b=aa(2)
k=-a
d=300;
v=d/exp(b)
cc=exp(b)*exp(a*t);
plot(t,c,'k+',t,cc,'r')
- 非线性最小二乘拟合
记 ,拟合准则是
,拟合准则是 的平方和最小,于是问题化为如下的优化问题
的平方和最小,于是问题化为如下的优化问题

(1)Matlab命令为
Lsqnonlin('f',a0)
其中,f.m是描述函数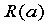 的函数文件名,
的函数文件名,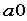 是初值
是初值
例 血药浓度问题
function f=ct(x)
t=[0.25,0.5,1,1.5,2,3,4,6,8];
c=[ 19.21,18.15,15.36,14.10,12.89,9.32,7.45,5.24,3.01];
f=c-x(1)*exp(x(2)*t);
x0=[10,0.5]
lsqnonlin('ct',x0)
(2)lsqcurvefit('fun',a0,x,y,LB,UB)
其中,f.m是描述函数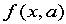 的函数文件名,
的函数文件名,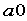 是初值,
是初值,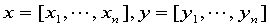 为数据
为数据
例 血药浓度问题
function f=xue(x,t)
f=x(1)*exp(x(2)*t);
t=[0.25,0.5,1,1.5,2,3,4,6,8];
c=[ 19.21,18.15,15.36,14.10,12.89,9.32,7.45,5.24,3.01];
x0=[10,0.5]
lsqcurvefit('xue',a0,t,c)
xuenon.m
t=[0.25,0.5,1,1.5,2,3,4,6,8];
c=[ 19.21,18.15,15.36,14.10,12.89,9.32,7.45,5.24,3.01];
lsqcurvefit('xue',a0,t,c);
yy=xue(x,t);
plot(t,c,'k*',t,yy,'r')
例 药物的吸收与排除(口服)
假设口服剂量为d,中心室血药浓度数据为
t=0.083,0.167,0.25,0.50,0.75,1.0,1.5,2.25,3.0,4.0,6.0,8.0,10.0,12.0
c=10.9,21.1,27.3,36.4,35.5,38.4,34.8,24.2,23.6,15.7,8.2,8.3,2.2,1.8
由机理分析(吸收室-中心室模型)得,中心室的血药浓度
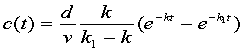
其中排除速率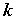 和吸收速率
和吸收速率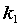 由上述数据拟合
由上述数据拟合
function f=xipai(x,t)
f=x(1)*x(3)*(exp(-x(2)*t)-exp(-x(1)*t))/(x(1)-x(2));
xipainon.m
t=[0.083,0.167,0.25,0.50,0.75,1.0,1.5,2.25,3.0,4.0,6.0,8.0,10.0,12.0];
c=[10.9,21.1,27.3,36.4,35.5,38.4,34.8,24.2,23.6,15.7,8.2,8.3,2.2,1.8];
x0=[1,0,40];
x=lsqcurvefit('xipai',x0,t,c);
yy=xipai(x,t);
plot(t,c,'k*',t,yy,'r')
3.14 回归分析
回归分析主要是对拟合问题作统计分析, 研究如下问题:①建立因变量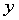 与自变量
与自变量 之间的回归模型(经验公式)②对回归模型的可信度进行检验③判断每个自变量
之间的回归模型(经验公式)②对回归模型的可信度进行检验③判断每个自变量 对
对 的影响是否显著④诊断回归模型是否适合这组数据⑤利用回归模型对
的影响是否显著④诊断回归模型是否适合这组数据⑤利用回归模型对 进行预报和控制.
进行预报和控制.
3.14.1多元线性回归
回归分析中最简单的形式
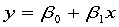
其中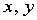 均为标量,
均为标量,  为回归系数,称为一元线性回归.一般地
为回归系数,称为一元线性回归.一般地
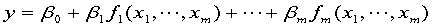
其中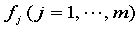 是已知函数. 这里
是已知函数. 这里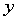 对回归系数
对回归系数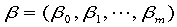 是线性的, 称为多元线性回归. 特别,
是线性的, 称为多元线性回归. 特别,  , 则
, 则

MATLAB实现
①b=regress(y,x)
其中
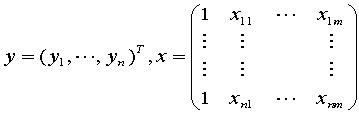
②[b,bint,r,rint,stats]=regress(y,x,alpha)
这里alpha为显著性水平(缺省时为0.05), b,bint为回归系数估计值和它们的置信区间, r,rint为残差及其置信区间, stats是用于检验回归模型的统计量,有三个值, 第一个是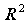 ,第二个是F, 第三个是与F对应的概率P, P<a时拒绝
,第二个是F, 第三个是与F对应的概率P, P<a时拒绝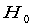 回归模型成立.
回归模型成立.
③rcoplot(r,rint) %残差及其置信区间图
例 合金强度与碳含量
下表是生产中收集的合金的强度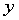 与其中的碳含量
与其中的碳含量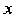 的数据
的数据
x | 0.10 0.11 0.12 0.13 0.14 0.15 0.16 0.17 0.18 0.20 0.21 0.23 |
y | 42.0 41.5 45.0 45.5 45.0 47.5 49.0 55.0 50.0 55.0 55.5 60.5 |
拟合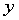 与
与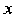 的函数关系,检验可信度,检查数据中有无异常点
的函数关系,检验可信度,检查数据中有无异常点
回归模型为
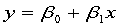
Hjt.m
--------------------------------------
x1=0.1:0.01:0.18;
x=[x1 0.2 0.21 0.23]';
y=[42.0 41.5 45.0 45.5 45.0 47.5 49.0 55.0 50.0 55.0 55.5 60.5]';
x=[ones(12,1) x];
[b,bint,r,rint,stats]=regress(y,x);
b,bint,stats,rcoplot(r,rint)
------------------------------------------------
b =
27.0269
140.6194
bint =
22.3226 31.7313
111.7842 169.4546
stats =
0.9219 118.0670 0.0000
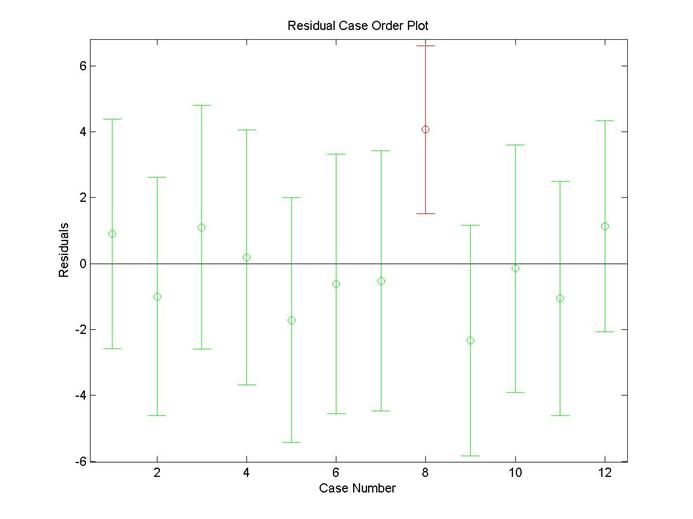
例 商品销售量与价格
某厂生产的一种商品的销售量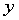 与竞争对手的价格
与竞争对手的价格 和本厂的价格
和本厂的价格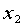 有关,某城市的销售记录如下
有关,某城市的销售记录如下
| 120 140 190 130 155 175 125 145 180 150 |
| 100 110 90 150 210 150 250 270 300 250 |
| 102 100 120 77 46 93 26 69 65 85 |
试根据这些数据建立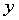 与
与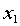 和
和 的关系式,对得到的模型和系数进行检验
的关系式,对得到的模型和系数进行检验
回归模型为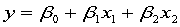
xljg.m
x1=[120 140 190 130 155 175 125 145 180 150]';
x2=[100 110 90 150 210 150 250 270 300 250]';
y=[102 100 120 77 46 93 26 69 65 85]';
x=[ones(10,1) x1 x2];
[b,bint,r,rint,stats]=regress(y,x);
b,bint,stats,rcoplot(r,rint)
检验结果模型不能用
3.14.2多元二项式回归
MATLAB的统计工具箱提供了一个作多元二项式回归的命令rstool, 它产生一个交互式画面, 并输出有关信息. 具体用法如下:
rstool(x,y,model,alpha)
其中 为输入数据, alpha为显著水平, model选择如下:
为输入数据, alpha为显著水平, model选择如下:
'linear':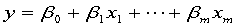 (线性模型)
(线性模型)
'purequadratic':  (纯二次)
(纯二次)
'interaction': 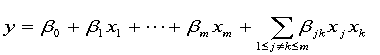 (交叉)
(交叉)
'quadratic': 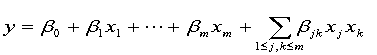 (完全二次)
(完全二次)
例 商品销售量与价格
某厂生产的一种商品的销售量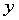 与竞争对手的价格
与竞争对手的价格 和本厂的价格
和本厂的价格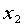 有关,某城市的销售记录如下
有关,某城市的销售记录如下
| 120 140 190 130 155 175 125 145 180 150 |
| 100 110 90 150 210 150 250 270 300 250 |
| 102 100 120 77 46 93 26 69 65 85 |
试根据这些数据建立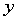 与
与 和
和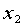 的关系式,对得到的模型和系数进行检验
的关系式,对得到的模型和系数进行检验
选择纯二次模型,即
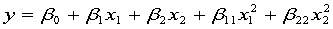
xljg1.m
x1=[120 140 190 130 155 175 125 145 180 150]';
x2=[100 110 90 150 210 150 250 270 300 250]';
y=[102 100 120 77 46 93 26 69 65 85]';
x=[x1 x2];
rstool(x,y,'purequadratic')
3.14.3非线性回归
非线性回归是指因变量 对回归系数
对回归系数 (而不是自变量)是非线性的,MATLAB的统计工具箱的如下命令可实现非线性回归:
(而不是自变量)是非线性的,MATLAB的统计工具箱的如下命令可实现非线性回归:
nlinfit
nlparci
nlpredci
nlintool
例 化学反应速度与反应物含量
在研究化学动力学反应过程中,建立了一个化学反应速度与反应物含量的数学模型

其中 是参数,
是参数,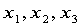 是三种反应物的含量,y是反应速度.今测得一组数据,试由此确定参数
是三种反应物的含量,y是反应速度.今测得一组数据,试由此确定参数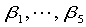 ,并给出置信区间.
,并给出置信区间.
序号 | |
y | 8.55 3.79 4.82 0.02 2.75 14.39 2.54 4.35 13.00 8.50 0.05 11.32 3.13 |
x1 | 470 285 470 470 470 100 100 470 100 100 100 285 285 |
x2 | 300 80 300 80 80 190 80 190 300 300 80 300 190 |
x3 | 10 10 120 120 10 10 65 65 54 120 120 10 120 |
Huaxue1.m
function yhat=huaxue1(beta,x)
b1=beta(1);b2=beta(2);b3=beta(3);b4=beta(4);b5=beta(5);
x1=x(:,1);x2=x(:,2);x3=x(:,3);
yhat=(b1*x2-x3/b5)./(1+b2*x1+b3*x2+b4*x3);
huaxue.m
x1=[470 285 470 470 470 100 100 470 100 100 100 285 285]';
x2=[300 80 300 80 80 190 80 190 300 300 80 300 190]';
x3=[10 10 120 120 10 10 65 65 54 120 120 10 120]';
y=[8.55 3.79 4.82 0.02 2.75 14.39 2.54 4.35 13.00 8.50 0.05 11.32 3.13]';
x=[x1 x2 x3];
beta=[1 0.05 0.02 0.1 2];
[betahat,f,J]=nlinfit(x,y,'huaxue1',beta);
betaci=nlparci(betahat,f,J);
betaa=[betahat,betaci]
[yhat,delta]=nlpredci('huaxue1',x,betahat,f,J);
yy=[y,yhat,delta]