14.8 三角Bézier曲面的直角坐标表示
二元多项式的标准形式之一是幂基表示,即:
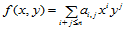 (14.8.1)
(14.8.1)
这可按Taylor展开重写如下:
 (14.8.2)
(14.8.2)
值得注意的是,偏导数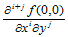 是关于方向
是关于方向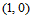 和
和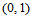 的方向导数。同样,若
的方向导数。同样,若 轴和
轴和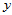 轴不正交时,上式仍然成立。由此,对于三角域上的三角Bézier曲面
轴不正交时,上式仍然成立。由此,对于三角域上的三角Bézier曲面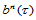 ,若令
,若令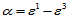 ,
,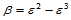 ,则有:
,则有:
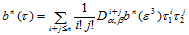 (14.8.3)
(14.8.3)
混合方向导数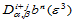 计算如下:
计算如下:
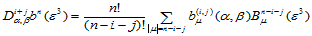
结合(14.8.1)和(14.8.3),有:
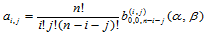
因为方向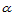 和
和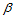 平行于域三角形的边,所以
平行于域三角形的边,所以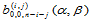 可由向前差分计算求得:
可由向前差分计算求得:
 (14.8.4)
(14.8.4)
为获得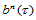 关于直角坐标
关于直角坐标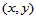 的幂基表示,只需将
的幂基表示,只需将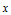 轴和
轴和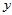 轴方向用重心坐标表示即可。设
轴方向用重心坐标表示即可。设 方向和
方向和 方向的重心坐标分别为
方向的重心坐标分别为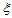 、
、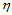 ,则:
,则:
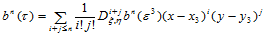 (14.8.5)
(14.8.5)
其中,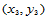 是顶点
是顶点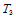 的
的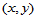 坐标。
坐标。
14.9 三角Bézier曲面的凸性
定义在三角形 上的函数设
上的函数设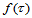 称为凸的,如果对
称为凸的,如果对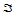 中任一点
中任一点 和任一方向
和任一方向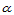 ,都有:
,都有:
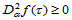 (14.9.1)
(14.9.1)
这一定义仅当 时有效,而对不满足这一条件的函数来说,其凸性定义如下:
时有效,而对不满足这一条件的函数来说,其凸性定义如下:
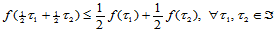 (14.9.2)
(14.9.2)
当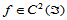 时,这两个定义等价。
时,这两个定义等价。
记三角形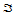 三个边方向如下:
三个边方向如下:
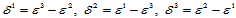
关于它们的方向导数算子记为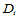 ,即:
,即: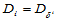 。那么,对任一方向
。那么,对任一方向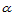 ,都有:
,都有:
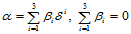
则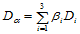 。混合偏导数表示为:
。混合偏导数表示为:
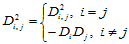 (14.9.3)
(14.9.3)
这里选择"−"表示从一个顶点到其余顶点的方向。由此,关于任一方向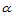 的二阶导数可表示为:
的二阶导数可表示为: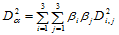 (14.9.4)
(14.9.4)
算子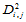 是对称的,即
是对称的,即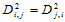 且满足条件:
且满足条件:
 (14.9.5)
(14.9.5)
证明 仅以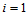 为例给出证明过程。
为例给出证明过程。
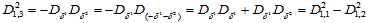
基于以上的讨论,我们有下述结果。
定理14.9
对于定义在三角形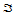 上的
上的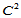 函数
函数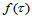 ,若满足条件:
,若满足条件:
 (14.9.6)
(14.9.6)
则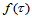 在
在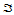 上是凸的。
上是凸的。
证明 对任一方向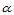 ,由式(14.9.4)和(14.9.5)可知
,由式(14.9.4)和(14.9.5)可知

故结论成立。
定理14.10 三角域 上的Bézier曲面
上的Bézier曲面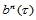 是凸曲面的充分条件是:
是凸曲面的充分条件是:
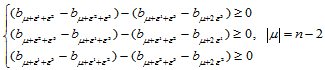 (14.9.7)
(14.9.7)
14.10 三角域上的插值Bézier曲面
本节讨论三角域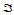 上的插值格式以及对用角点处的位置、导数和跨边界导数的插值问题。插值数据或者取自一二元函数
上的插值格式以及对用角点处的位置、导数和跨边界导数的插值问题。插值数据或者取自一二元函数 或者由数值估计而得。
或者由数值估计而得。
14.10.1 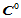 三次插值(九参数插值
三次插值(九参数插值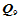 )
)
在域三角形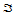 的每个顶点处给定位置和两个边方向的导数,例如在
的每个顶点处给定位置和两个边方向的导数,例如在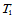 处给定数据:
处给定数据:
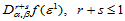 (14.10.1)
(14.10.1)
这里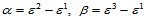 。其余两个顶点
。其余两个顶点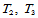 处给定的数据类似。由此可构造一三次Bézier曲面,使其满足插值条件(14.10.1)。边界上的九个Bézier纵标确定如下:在点
处给定的数据类似。由此可构造一三次Bézier曲面,使其满足插值条件(14.10.1)。边界上的九个Bézier纵标确定如下:在点 处:
处:
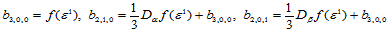 (14.10.2)
(14.10.2)
利用点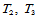 处的插值信息,亦可确定出
处的插值信息,亦可确定出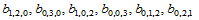 。
。
Bézier纵标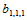 不能由给定的插值信息确定,可任意取值。
不能由给定的插值信息确定,可任意取值。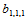 的合理选择是使插值格式具有二次精度,即若给定的九个插值数据取自一二次曲面,那么插值的结果是再现这一二次曲面。由此,
的合理选择是使插值格式具有二次精度,即若给定的九个插值数据取自一二次曲面,那么插值的结果是再现这一二次曲面。由此,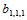 可选取如下:
可选取如下:
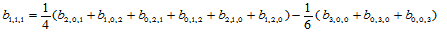 (14.10.3)
(14.10.3)
按照式(14.10.3)确定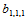 ,则保证插值格式具有二次精度。当然,其他的选择
,则保证插值格式具有二次精度。当然,其他的选择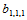 的方法也能保证二次精度。那么哪一种选择是最好的?这是一个有待进一步研究的问题。
的方法也能保证二次精度。那么哪一种选择是最好的?这是一个有待进一步研究的问题。
当用九插值参数格式 构造组合曲面时,其致命的缺陷是要求
构造组合曲面时,其致命的缺陷是要求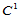 插值数据,但构造的组合曲面整体仅是
插值数据,但构造的组合曲面整体仅是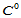 连续的。
连续的。
14.10.2 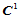 五次插值(21参数插值
五次插值(21参数插值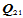 )
)
为了得到整体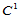 连续的插值曲面,就需给定更多的插值数据,即在三角形
连续的插值曲面,就需给定更多的插值数据,即在三角形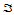 的每个顶点处给出直到二阶的导数信息,以及每条边的中点处的跨边界导数。例如在
的每个顶点处给出直到二阶的导数信息,以及每条边的中点处的跨边界导数。例如在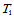 处给定数据:
处给定数据:
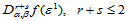 (14.10.4)
(14.10.4)
在边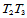 的中点处给定跨边界导数:
的中点处给定跨边界导数:
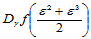 (14.10.5)
(14.10.5)
这里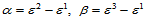 ,
,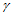 为不平行于边
为不平行于边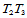 的任一方向。其余两个顶点
的任一方向。其余两个顶点 和两条边中点处给定的数据类似。
和两条边中点处给定的数据类似。
这样以来,给定的插值数据共有21个,而五次三角Bézier曲面的Bézier纵标也有21个,由此,可惟一确定一五次三角Bézier曲面。例如由角点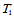 处的插值数据可确定下述的Bézier纵标(图14.9):
处的插值数据可确定下述的Bézier纵标(图14.9):

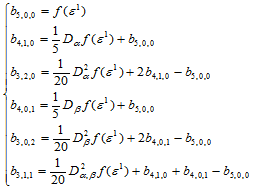 (14.10.6)
(14.10.6)
由边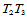 的中点处给定跨边界导数可确定Bézier纵标
的中点处给定跨边界导数可确定Bézier纵标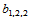 。由导数公式可知:
。由导数公式可知:
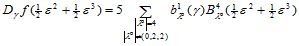
从而
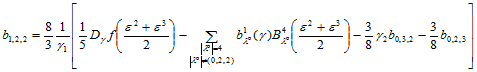 (14.10.7)
(14.10.7)
式(14.10.7)只有当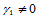 时才有意义,即方向
时才有意义,即方向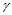 不平行于边
不平行于边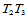 。通常选择方向
。通常选择方向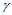 为边
为边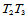 的垂线方向:
的垂线方向:

其中,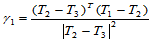 。
。
由角点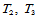 处的插值信息,以及边
处的插值信息,以及边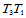 、
、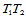 中点处的跨边界导数信息亦可确定出剩余的14个Bézier纵标。
中点处的跨边界导数信息亦可确定出剩余的14个Bézier纵标。
一般情况下,跨边界导数不易给定。在此情况下,人们通常采用另外的称之为参数凝聚(condensation of parameters)的方法:五次三角Bézier曲面在三条边界上的跨边界导数都是四次多项式,将其用三次多项式替代,那么,由四次项系数为零的条件可得到三个方程。由此可求出未知的Bézier纵标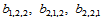 。例如,对于边界
。例如,对于边界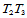 ,曲面
,曲面 的跨边界导数为:
的跨边界导数为:
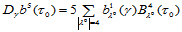
由四次项系数为零的条件,有:
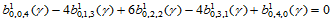 (14.10.8)
(14.10.8)
因此
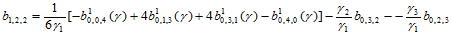 (14.10.9)
(14.10.9)
利用这种方法构造五次插值曲面,我们只需提供18个插值数据,因而这一插值格式也称做18参数插值,记为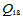 。
。
五次18 参数插值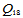 具有局部性:一个数据点处插值数据的修改仅影响到共有这一数据点的那些三角形上的插值曲面。
具有局部性:一个数据点处插值数据的修改仅影响到共有这一数据点的那些三角形上的插值曲面。
当用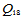 、
、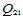 格式构造组合曲面时,其整体达到
格式构造组合曲面时,其整体达到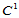 连续。
连续。
一般情况下,若在三角形网格的每一个角点处给定了直到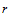 阶的方向导数,那么插值于这些数据的分片多项式曲面整体达到
阶的方向导数,那么插值于这些数据的分片多项式曲面整体达到 连续的必要条件是分片多项式的次数
连续的必要条件是分片多项式的次数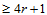 。
。
证明 由插值条件可确定出三角形顶点处的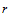 阶子网(图14.10)。由于要求跨边界
阶子网(图14.10)。由于要求跨边界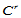 连续,我们必须指定平行于边界的
连续,我们必须指定平行于边界的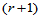 排Bézier纵标,它们由跨边界方向导数所确定。而跨边界方向导数由具有公共边界的两个三角形共享。因此,跨边界
排Bézier纵标,它们由跨边界方向导数所确定。而跨边界方向导数由具有公共边界的两个三角形共享。因此,跨边界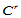 连续。然而除非特殊情形,一般地,图14.10中红色三角形部分的Bézier纵标为相互冲突的跨边界导数所确定。因此,为了使这些Bézier纵标惟一确定,必须在三角形的每一顶点处给定直到
连续。然而除非特殊情形,一般地,图14.10中红色三角形部分的Bézier纵标为相互冲突的跨边界导数所确定。因此,为了使这些Bézier纵标惟一确定,必须在三角形的每一顶点处给定直到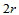 阶的方向导数。要使这些导数信息相一致的插值多项式至少是
阶的方向导数。要使这些导数信息相一致的插值多项式至少是 阶的。
阶的。
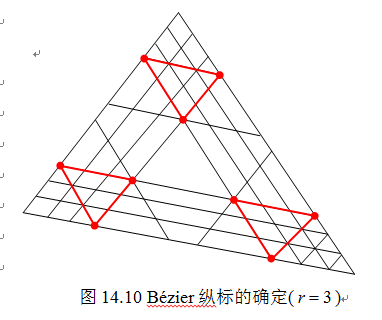
值得注意的是,对 ,在三角形顶点处给定直到
,在三角形顶点处给定直到 阶的方向导数和跨边界的
阶的方向导数和跨边界的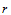 阶的方向导数后,并不能惟一确定一插值多项式,因为还有
阶的方向导数后,并不能惟一确定一插值多项式,因为还有 个Bézier纵标是任意的。尽管不影响曲面整体的光滑性,但应恰当地选择以产生"好"的局部插值格式。若不能从被插函数获得更多的信息,应确定自由的Bézier纵标以使插值格式的多项式精度尽可能高。
个Bézier纵标是任意的。尽管不影响曲面整体的光滑性,但应恰当地选择以产生"好"的局部插值格式。若不能从被插函数获得更多的信息,应确定自由的Bézier纵标以使插值格式的多项式精度尽可能高。
同样,若不能提供足够的跨边界方向导数信息来确定平行于边界的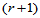 排Bézier纵标,亦可采用前述的参数聚集法。当然,此时不仅对一阶跨边界导数,而且对直到
排Bézier纵标,亦可采用前述的参数聚集法。当然,此时不仅对一阶跨边界导数,而且对直到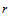 阶的跨边界导数。
阶的跨边界导数。
五次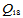 和
和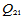 插值格式是上述一般情况的特例(
插值格式是上述一般情况的特例(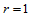 )。
)。
14.10.3 剖分插值
前述的插值格式有一个共同的缺陷,那就是为获得要求的连续阶的组合曲面,必须提供比连续阶更高阶的导数信息。比如,由二阶导数信息建立的插值曲面格式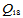 和
和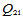 仅获得了
仅获得了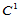 连续的曲面,这显然是不经济的。
连续的曲面,这显然是不经济的。
本小节的目标是提供一种插值格式,它所要求的插值数据与连续阶相匹配,即要求的导数信息不高于插值曲面的连续阶。这就是Clough-Tocher插值格式。
1. 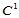 Clough-Tocher插值格式
Clough-Tocher插值格式
Clough-Tocher插值格式是所有基于剖分三角形的插值格式中最简单的一种,在有限元分析中得到广泛应用。其构造原理如下:
在三角形顶点处给定函数值、两个边方向的导数,以及每条边中点处的法方向导数,将三角形 用形心分割成三个子三角形(图14.11)。在每一个子三角形上构造一三次插值曲面,使得在
用形心分割成三个子三角形(图14.11)。在每一个子三角形上构造一三次插值曲面,使得在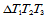 上的组合曲面
上的组合曲面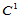 连续。
连续。
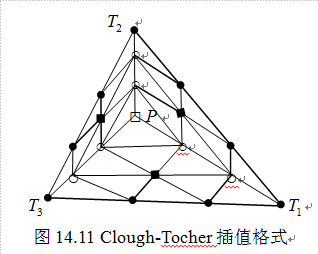
由已知插值条件,三条边界上的九个Bézier纵标可惟一确定。由跨边界法方向导数可确定图14.11中标记为"♦"处的Bézier纵标。其余标记为"○"和"□"的Bézier纵标则由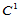 连续性条件惟一确定。
连续性条件惟一确定。
Clough-Tocher插值格式基于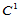 数据构造了
数据构造了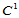 的插值曲面,只要求12个插值数据。对于许多应用来说,一般仅提供三角形顶点处的九个数据,并未给出边中点处的跨边界法方向导数。在这种情况下,可采用数值方法估计其法方向导数。例如,要求插值曲面在边界上的跨边界方向导数是一次的,也可以先构造
的插值曲面,只要求12个插值数据。对于许多应用来说,一般仅提供三角形顶点处的九个数据,并未给出边中点处的跨边界法方向导数。在这种情况下,可采用数值方法估计其法方向导数。例如,要求插值曲面在边界上的跨边界方向导数是一次的,也可以先构造 插值格式,然后计算其边界中点处的跨边界法方向导数等。
插值格式,然后计算其边界中点处的跨边界法方向导数等。
尽管Clough-Tocher插值格式构造的插值曲面在每一个三角形上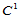 连续,但有以下重要的结果。
连续,但有以下重要的结果。
定理14.11
在三角形形心处,Clough-Tocher插值曲面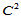 连续。
连续。
为了证明该定理,我们引下述引理。
引理14.3 基于Clough-Tocher三角形剖分构造的 分片二次多项式曲面是
分片二次多项式曲面是 连续的,即它们是同一张二次曲面。
连续的,即它们是同一张二次曲面。
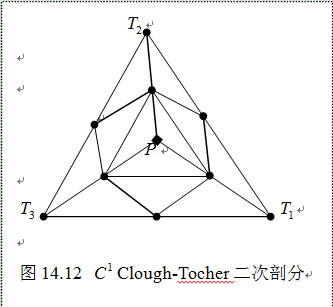
证明 对于给定的三角形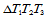 ,以形心为分割点将其分割成三个子三角形(图14.12)。在每一个子三角形上构造一二次曲面,使其组合曲面
,以形心为分割点将其分割成三个子三角形(图14.12)。在每一个子三角形上构造一二次曲面,使其组合曲面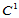 连续。
连续。
假定给定子三角形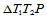 上二次曲面的六个Bézier纵标,那么根据
上二次曲面的六个Bézier纵标,那么根据 连续性条件,图14.12中标记为"●"的Bézier纵标被惟一确定。进而,标记为"♦"的Bézier纵标也由
连续性条件,图14.12中标记为"●"的Bézier纵标被惟一确定。进而,标记为"♦"的Bézier纵标也由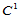 连续性条件惟一确定。因而,三张二次曲面片由六个Bézier纵标完全确定。由于任何三张
连续性条件惟一确定。因而,三张二次曲面片由六个Bézier纵标完全确定。由于任何三张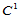 的二次曲面片可用这种方法构造,这表明定义在Clough-Tocher三角形剖分上的
的二次曲面片可用这种方法构造,这表明定义在Clough-Tocher三角形剖分上的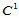 分片二次曲面的维数是6,而全体二次曲面的维数亦是6。注意到二次曲面是
分片二次曲面的维数是6,而全体二次曲面的维数亦是6。注意到二次曲面是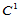 分片二次曲面空间的子集,故结论成立。
分片二次曲面空间的子集,故结论成立。
定理14.11的证明 由于形心处的直到二阶的方向导数仅依赖于去掉
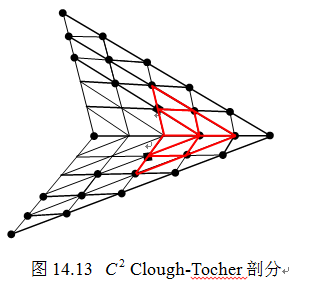
Bézier网边界的二阶子网,由插值曲面构造过程可知,它是一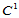 的分片二阶子网。由引理14.3,该
的分片二阶子网。由引理14.3,该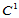 分片二阶子网表示的是整体二阶连续的。故形心处的二阶方向导数连续。
分片二阶子网表示的是整体二阶连续的。故形心处的二阶方向导数连续。
2. Clough-Tocher剖分的限制
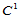 Clough-Tocher插值可刻画如下:①
在三角形的顶点处给定足够的数据以保证顶点处的
Clough-Tocher插值可刻画如下:①
在三角形的顶点处给定足够的数据以保证顶点处的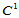 连续性;②
给定足够的跨边界方向导数信息以惟一确定
连续性;②
给定足够的跨边界方向导数信息以惟一确定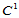 连续的跨边界导数。
连续的跨边界导数。
当然,人们自然希望用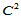 数据来替换
数据来替换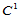 数据,以构造Clough-Tocher剖分上的
数据,以构造Clough-Tocher剖分上的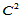 插值。遗憾的是,最终的插值将是超定的。
插值。遗憾的是,最终的插值将是超定的。
为了明确这一点,我们用图例予以说明。假设图14.13是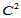 Clough-Tocher剖分插值的部分子网,那么每一子三角形上的曲面至少是五次的。由角点处的
Clough-Tocher剖分插值的部分子网,那么每一子三角形上的曲面至少是五次的。由角点处的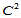 数据信息惟一确定出图中标记为"●"的Bézier纵标,而标记为"♦"的Bézier纵标则由跨边界
数据信息惟一确定出图中标记为"●"的Bézier纵标,而标记为"♦"的Bézier纵标则由跨边界 方向导数独立确定。
方向导数独立确定。
另一方面,根据 连续性条件,图中粗线区域中的控制网定义一二次曲面。由引理14.3,二次曲面由六个独立信息惟一确定。可是现在却有七个条件:平行三角形两条边的五个Bézier纵标和两个标记为"♦"的Bézier纵标。因此,我们提出的插值问题导致了由七个独立条件确定二次曲面,这显然是超定的。
连续性条件,图中粗线区域中的控制网定义一二次曲面。由引理14.3,二次曲面由六个独立信息惟一确定。可是现在却有七个条件:平行三角形两条边的五个Bézier纵标和两个标记为"♦"的Bézier纵标。因此,我们提出的插值问题导致了由七个独立条件确定二次曲面,这显然是超定的。
这表明,为了获得剖分形式的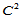 插值,① 必须在三角形的顶点处给定至少
插值,① 必须在三角形的顶点处给定至少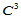 的数据;②
或者采用一种在三角形顶点处至少有三个子三角形的剖分格式。
的数据;②
或者采用一种在三角形顶点处至少有三个子三角形的剖分格式。
Sablonniére研究了第一种格式,他在Clough-Tocher剖分上用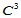 数据构造
数据构造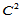 七次分片多项式曲面。Alleld则讨论了第二种格式,他采用递归的Clough-Tocher剖分,即对三角形进行一次Clough-Tocher剖分后,再对每一子三角形进行一次Clough-Tocher剖分。这样便有足够的自由度用于
七次分片多项式曲面。Alleld则讨论了第二种格式,他采用递归的Clough-Tocher剖分,即对三角形进行一次Clough-Tocher剖分后,再对每一子三角形进行一次Clough-Tocher剖分。这样便有足够的自由度用于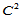 分片五次插值曲面的构造。尽管求解了
分片五次插值曲面的构造。尽管求解了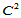 插值问题,但所得插值曲面却呈现了不期望的振荡。
插值问题,但所得插值曲面却呈现了不期望的振荡。
3. 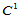 Powell-Sabin插值格式
Powell-Sabin插值格式
Powell-Sabin方法用三角形顶点处的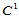 数据构造了
数据构造了 分片二次插值曲面,其做法是对三角形进行剖分,剖分后子三角形的数目取决于三角形的几何形状。
分片二次插值曲面,其做法是对三角形进行剖分,剖分后子三角形的数目取决于三角形的几何形状。
① 如果三角形所有内角均小于750,将三角形剖分成六个子三角形。剖分过程是,首先用三角形外接圆的圆心将三角形分割成三个子三角形,然后连接边的中点和外接圆的圆心,如图14.14所示。那么根据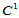 连续条件,可求出标记为"●"的Bézier纵标。标记为"♦"的Bézier纵标为两个标记为"●"的Bézier纵标的平均值。标记为"■"的Bézier纵标则是围绕它的标记为"♦"的Bézier纵标所构成三角形的外接圆圆心。
连续条件,可求出标记为"●"的Bézier纵标。标记为"♦"的Bézier纵标为两个标记为"●"的Bézier纵标的平均值。标记为"■"的Bézier纵标则是围绕它的标记为"♦"的Bézier纵标所构成三角形的外接圆圆心。
由这一分割的特殊性,使得跨边界导数沿三角形的边界计算时是线性的,而非分段线性。因此,保证了由此构造的组合二次曲面的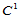 连续性。这一论断的正确性归结于以下事实:连接两个相邻三角形(具有公共边)的外接圆的圆心的线恰好交于公共边界的中点处。
连续性。这一论断的正确性归结于以下事实:连接两个相邻三角形(具有公共边)的外接圆的圆心的线恰好交于公共边界的中点处。
② 如果三角形的内角不满足小于750的条件,则将三角形剖分成十二个子三角形:用形心和边的中点进行剖分三角形如图14.15所示。那么,定义十二片二次曲面的Bézier纵标可由三角形顶点处的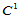 数据以及
数据以及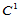 连续性条件确定如下:
连续性条件确定如下:
(a)"●":由给定的数据确定;
(b)"▲":由线性跨边界导数确定;
(c)"♦":位于"●"和"▲"连线的中点处;

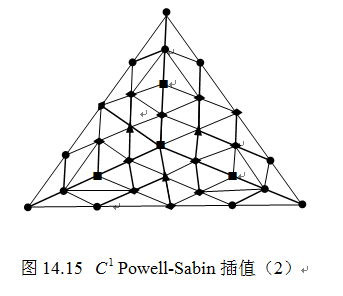
(d)"■":位于周围"♦"的平面内。
14.11 参数型三角Bézier曲面
前面讨论的三角曲面实质上是从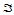 到
到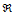 的影射,其产生的曲面具有显式表达式
的影射,其产生的曲面具有显式表达式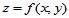 或
或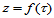 。这显然不能满足实际工程应用的需要,因此本节讨论参数型三角Bézier曲面。
。这显然不能满足实际工程应用的需要,因此本节讨论参数型三角Bézier曲面。
设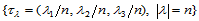 为三角域
为三角域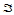 的分割,给定三维空间
的分割,给定三维空间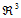 中
中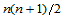 个点
个点 ,矢值函数:
,矢值函数:
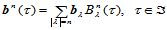 (14.11.1)
(14.11.1)
称为定义在三角形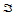 上的
上的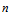 次参数三角Bézier曲面,其中
次参数三角Bézier曲面,其中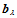 称为曲面
称为曲面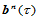 的控制顶点或Bézier点,其构成的分片线性曲面BL叫做
的控制顶点或Bézier点,其构成的分片线性曲面BL叫做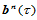 的控制网格或Bézier网(图14.16)。
的控制网格或Bézier网(图14.16)。

14.11.1 参数三角Bézier曲面的性质与求值
参数三角Bézier曲面是三角Bézier曲面的直接推广,因此继承了三角Bézier曲面的一系列性质,其求值和求方向导数以及生阶、分割等均与三角曲面片相同,我们这里不再重复。
14.11.2 参数连续性
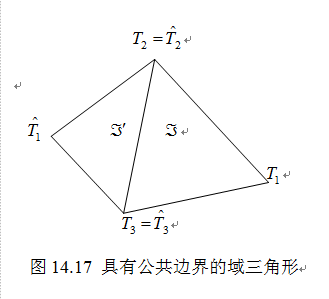
设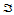 和
和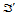 为两个具有公共边界的域三角形(图14.17),
为两个具有公共边界的域三角形(图14.17),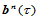 和
和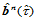 分别为定义在
分别为定义在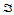 和
和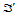 上的参数三角曲面片。
上的参数三角曲面片。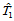 关于
关于 的重心坐标为
的重心坐标为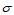 。那么,
。那么,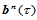 和
和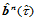 在公共参数边界上
在公共参数边界上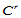 连续的充分必要条件是:
连续的充分必要条件是:
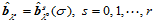 (14.14.1)
(14.14.1)
其中的符号与前述完全相同,只不过这里的是点而不是标量.
14.11.3 几何连续性
由于参数三角曲面完全由它的Bézier网所决定,至于域三角形是什么形状无关紧要。因此,我们应当用相邻的两个参数三角Bézier曲面片的Bézier网来描述其连续性。
设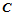 是
是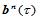 和
和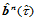 的公共边界曲线上一点,则,点
的公共边界曲线上一点,则,点 按de Casteljau算法可由任一张曲面片求的点
按de Casteljau算法可由任一张曲面片求的点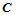 。根据de Casteljau算法,中间点
。根据de Casteljau算法,中间点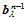 和
和 分别确定两张曲面在点
分别确定两张曲面在点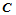 处的切平面。要使
处的切平面。要使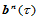 和
和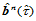 在点
在点 处
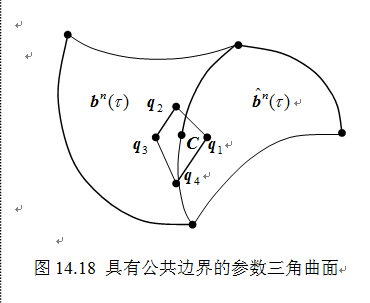
处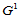 连续,其切平面应当一致。若将所设计的顶点标记如下(图14.18):
连续,其切平面应当一致。若将所设计的顶点标记如下(图14.18):
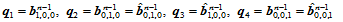
则,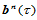 和
和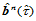 沿公共边界曲线
沿公共边界曲线 连续的条件是:
连续的条件是:
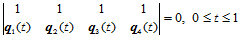 (14.14.2)
(14.14.2)