11.8 Bézier曲面的矩阵表示
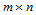 次Bézier曲面可用矩阵表示如下:
次Bézier曲面可用矩阵表示如下:
 (11.8.1)
(11.8.1)
利用矩阵表示式,我们便可实现不同多项式基之间的转换。比如,为了采用高效的Horner格式进行Bézier曲面计算,就需要将Bézier曲面表示成幂基的形式,那么就有:
 (11.8.2)
(11.8.2)
其中,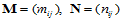 分别是
分别是 阶和
阶和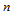 阶方阵:
阶方阵:
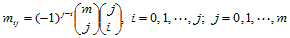 (11.8.3)
(11.8.3)
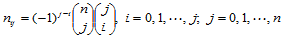 (11.8.4)
(11.8.4)
11.9 Bézier曲面片的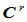 连续性
连续性
设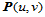 是定义在区域
是定义在区域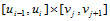 上的一张
上的一张 次Bézier曲面,其控制顶点是
次Bézier曲面,其控制顶点是 ,
, 是定义在区域
是定义在区域 上的另一张
上的另一张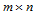 次Bézier曲面,其控制顶点是
次Bézier曲面,其控制顶点是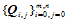 ,两张曲面具有公共参数边界
,两张曲面具有公共参数边界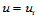 。那么,由
。那么,由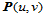 和
和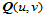 构成的组合曲面片在公共参数边界
构成的组合曲面片在公共参数边界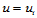 上
上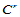 连续的充分必要条件是:
连续的充分必要条件是:
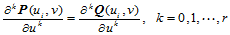 (11.9.1)
(11.9.1)
根据Bézier曲面的偏导矢计算公式(11.6.1)可知
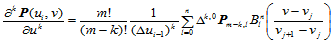

即:
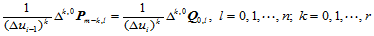 (11.9.2)
(11.9.2)
这恰好就是组合Bézier曲线的 连续性条件在组合Bézier曲面控制网格的
连续性条件在组合Bézier曲面控制网格的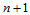 行顶点上的应用。因此,组合Bézier曲面跨公共参数边界
行顶点上的应用。因此,组合Bézier曲面跨公共参数边界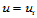 的
的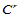 连续性条件可陈述如下:
连续性条件可陈述如下:
两具有公共参数边界的 次Bézier曲面片跨边界
次Bézier曲面片跨边界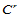 连续,当且仅当组合Bézier网的每一行控制顶点构成
连续,当且仅当组合Bézier网的每一行控制顶点构成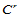 连续的Bézier曲线的控制多边形。
连续的Bézier曲线的控制多边形。
对于参数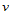 ,类似的条件也成立。
,类似的条件也成立。
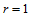 时,即一阶参数连续,其相应两张Bézier曲面的控制顶点满足条件:
时,即一阶参数连续,其相应两张Bézier曲面的控制顶点满足条件:
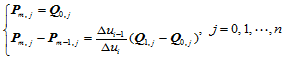 (11.9.3)
(11.9.3)
这表明,两张Bézier曲面片不仅具有公共的边界曲线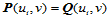 ,而且在公共边界上还具有公共的切平面。进而,相继三个控制顶点
,而且在公共边界上还具有公共的切平面。进而,相继三个控制顶点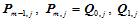 共线且定比
共线且定比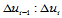 对每一行都成立。
对每一行都成立。
以上只是讨论了特殊情况下的组合Bézier曲面沿公共参数边界跨边界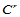 连续的条件。事实上,曲面片的光滑连续拼接远比曲线复杂得多。两张具有公共参数边界的Bézier曲面可能次数不一致,也可能只具有部分公共参数边界,或许两张Bézier曲面片没有公共参数边界,但却有公共的边界曲线。那么,如何度量它们之间的光滑性呢?对于第一种和第二种情形,我们可通过Bézier曲面的升阶技术和分割技术,使两张Bézier曲面次数一致,且具有公共参数边界。而在第三种情形下,则必须通过公共连接线处两张Bézier曲面关于各自参数的偏导矢来度量光滑性。由此,可建立参数连续性的定义。
连续的条件。事实上,曲面片的光滑连续拼接远比曲线复杂得多。两张具有公共参数边界的Bézier曲面可能次数不一致,也可能只具有部分公共参数边界,或许两张Bézier曲面片没有公共参数边界,但却有公共的边界曲线。那么,如何度量它们之间的光滑性呢?对于第一种和第二种情形,我们可通过Bézier曲面的升阶技术和分割技术,使两张Bézier曲面次数一致,且具有公共参数边界。而在第三种情形下,则必须通过公共连接线处两张Bézier曲面关于各自参数的偏导矢来度量光滑性。由此,可建立参数连续性的定义。
定义11.1 当且仅当两张Bézier曲面 沿它们的公共连接线
沿它们的公共连接线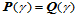 处处具有直到
处处具有直到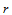 阶的连续偏导矢,则称它们沿公共连接线
阶的连续偏导矢,则称它们沿公共连接线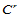 连续,即:
连续,即:
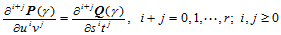 (11.9.4)
(11.9.4)
这里,公共连接线 应理解为曲面上的曲线,它不必一定要是曲面上的等参数线,后者只是它的特殊情况。
应理解为曲面上的曲线,它不必一定要是曲面上的等参数线,后者只是它的特殊情况。
特别地,若两曲面片 都定义在单位矩形区域上,且公共连接线就是两曲面的公共边界曲线
都定义在单位矩形区域上,且公共连接线就是两曲面的公共边界曲线 ,则它们沿该公共边界的
,则它们沿该公共边界的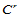 连续性条件就简化为:
连续性条件就简化为:
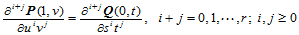 (11.9.5)
(11.9.5)
其中,两曲面沿公共边界曲线的直到 阶的偏导矢一致,即:
阶的偏导矢一致,即:

自然满足。那么,两曲面片是否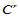 连续便取决于沿公共边界的直到
连续便取决于沿公共边界的直到 阶的偏导矢与混合偏导矢是否一致了。
阶的偏导矢与混合偏导矢是否一致了。
上述两曲面各自定义在局部参数域上,如果改取整体参数域,情况又不一样了。设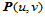 是定义在分割
是定义在分割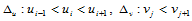 上的组合Bézier曲面,那么
上的组合Bézier曲面,那么 在
在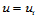 处
处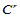 连续的条件为:
连续的条件为:
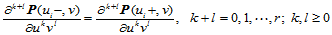 (11.9.6)
(11.9.6)
参数连续性总是与参数的选取有关,由于曲面不存在曲线那样的反映内在几何特征的弧长参数,使得曲面的参数连续性总是只在特定的参数下成立。如果对已经 连续的两曲面之一做参数变换,重新参数化后将不再是
连续的两曲面之一做参数变换,重新参数化后将不再是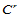 连续的。
连续的。
如果两曲面沿公共连接线是非正则的,尽管沿该连接线 连续,却有可能沿该连接线并非处处存在公共切平面。因而是不光滑的。两曲面沿公共连接线的最低阶光滑连接(一阶光滑)只需沿该连接线处处存在切平面,并不要求它们
连续,却有可能沿该连接线并非处处存在公共切平面。因而是不光滑的。两曲面沿公共连接线的最低阶光滑连接(一阶光滑)只需沿该连接线处处存在切平面,并不要求它们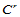 连续。可见,用参数连续来度量两曲面沿正则边界连接的光滑性是过分限制而不必要,它不能确切量度曲面连接的光滑度。
连续。可见,用参数连续来度量两曲面沿正则边界连接的光滑性是过分限制而不必要,它不能确切量度曲面连接的光滑度。
Bézier曲面片的几何连续性
11.10.1  连续性条件
连续性条件
两曲面的零阶几何连续,即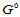 连续与
连续与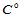 连续一致,
连续一致,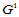 连续亦称做切平面连续定义如下:
连续亦称做切平面连续定义如下:
定义11.2
两参数曲面沿它们的公共连接线 连续,当且仅当它们沿该公共连接线处处具有公共的切平面或公共的曲面法线。
连续,当且仅当它们沿该公共连接线处处具有公共的切平面或公共的曲面法线。
设两曲面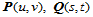 具有公共连接线
具有公共连接线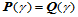 ,在公共连接线的每一点具有不重合的四个切矢
,在公共连接线的每一点具有不重合的四个切矢 。根据公共切平面之要求,四个切矢共面,所以:
。根据公共切平面之要求,四个切矢共面,所以:
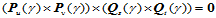
即:
 (11.10.1)
(11.10.1)
特别,当两曲面的公共连接线为两曲面的等参数线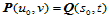 ,
, 时,在公共连接线上每一点都有
时,在公共连接线上每一点都有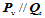 。于是,具有公共切平面的条件便简化为:
。于是,具有公共切平面的条件便简化为:
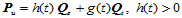 (11.10.2)
(11.10.2)
这里假定两跨边界切矢 之一的方向指向公共等参数线而另一个背离公共等参数线,那么
之一的方向指向公共等参数线而另一个背离公共等参数线,那么 保证两曲面在公共等参数线上处处不打皱。
保证两曲面在公共等参数线上处处不打皱。
若 ,则表明曲面
,则表明曲面 的
的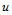 线与
线与 的
的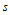 线跨公共等参数线
线跨公共等参数线 连续,若又
连续,若又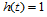 ,则进一步表明它们是
,则进一步表明它们是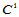 连续的。
连续的。
对于两张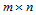 次Bézier曲面来说,为了保证曲面次数不变,函数
次Bézier曲面来说,为了保证曲面次数不变,函数 为常数,
为常数, 取线性函数。令
取线性函数。令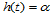 ,
, ,则两张Bézier曲面沿公共边界曲线
,则两张Bézier曲面沿公共边界曲线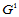 连续的充分必要条件是:
连续的充分必要条件是:
 (11.10.3)
(11.10.3)
简化即得:
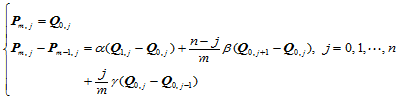 (11.10.4)
(11.10.4)
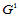 连续看似光滑,但反射线一般在公共连接处出现折弯。因此,在要求较高的场合,曲面片应该按曲率连续的方式拼接在一起,即达到
连续看似光滑,但反射线一般在公共连接处出现折弯。因此,在要求较高的场合,曲面片应该按曲率连续的方式拼接在一起,即达到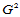 连续。
连续。
11.10.2 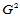 连续性条件
连续性条件
 连续亦称做曲率连续,它要求两曲面片沿公共连接线处处在所有方向上都具有公共的法曲率。因此,可定义如下:
连续亦称做曲率连续,它要求两曲面片沿公共连接线处处在所有方向上都具有公共的法曲率。因此,可定义如下:
定义11.3
两参数曲面沿它们的公共连接线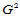 连续,当且仅当它们沿该公共连接线处处除具有公共切平面外,还具有公共的主曲率。在两个主曲率不相等时具有公共的主方向或一致的Dupin标线。
连续,当且仅当它们沿该公共连接线处处除具有公共切平面外,还具有公共的主曲率。在两个主曲率不相等时具有公共的主方向或一致的Dupin标线。
下面,我们按定义11.3建立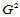 连续性条件。
连续性条件。
参数曲面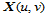 在任一点的法矢定义为:
在任一点的法矢定义为:
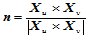
对切平面上任一方向 ,过点
,过点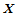 、法矢
、法矢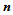 、方向
、方向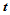 之平面与曲面的交线在点
之平面与曲面的交线在点 处的曲率称为曲面在给定方向
处的曲率称为曲面在给定方向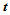 上的法曲率
上的法曲率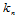 :
:

其中:
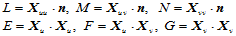
除非给定点处所有方向上的法曲率相同,否则点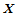 处存在相互垂直的两个方向,使得沿这两个方向的法曲率取得最大值
处存在相互垂直的两个方向,使得沿这两个方向的法曲率取得最大值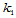 和最小值
和最小值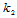 ,这两个方向称为主方向,
,这两个方向称为主方向,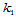 、
、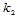 称为主曲率。那么,以这两个方向作为坐标轴
称为主曲率。那么,以这两个方向作为坐标轴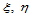 ,则法曲率
,则法曲率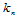 可表示为:
可表示为:
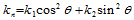
即:
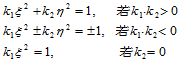
其中,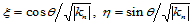 。
。
三个方程依次表示椭圆、共轭双曲线及平行直线,称为曲面在点 处的Dupin标线,曲面在一点任一方向上的法曲率由Dupin标线完全确定。
处的Dupin标线,曲面在一点任一方向上的法曲率由Dupin标线完全确定。
法曲率为零的方向称做渐近方向,其方程是:
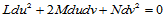
Dupin标线亦可由渐近方向和第三个方向上的法曲率惟一确定。由此,对于具有公共边界曲线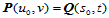 (
(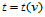 )的两张参数曲面
)的两张参数曲面 要达到
要达到 连续, 只要具有公共的渐近方向即可。
连续, 只要具有公共的渐近方向即可。
 在公共连接线上的渐近方向满足方程:
在公共连接线上的渐近方向满足方程:
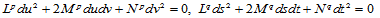
若两者表示同一渐近方向
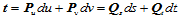
那么,由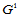 条件可知
条件可知
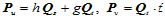
因此
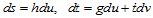
而
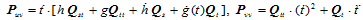
代入渐近线方程,便有:
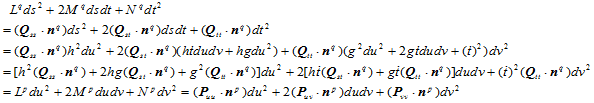
因在公共连接线上两曲面 连续,因而
连续,因而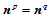 。故由上式可得:
。故由上式可得:
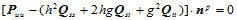
从而

故,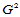 连续条件为:
连续条件为:
 (11.10.5)
(11.10.5)
对于两张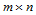 次的Bézier曲面来说,为了保证曲面次数不变,函数
次的Bézier曲面来说,为了保证曲面次数不变,函数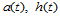 为常数,
为常数, ,
,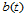 取线性函数。若令
取线性函数。若令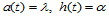 ,
, ,
,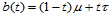 ,则两张Bézier曲面沿公共边界曲线
,则两张Bézier曲面沿公共边界曲线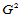 连续的条件是:
连续的条件是:
 (11.10.6)
(11.10.6)
化简后,即可得到关于Bézier点满足的一组关系式,它仅与公共边界曲线两侧各两排控制顶点相关。
11.10.3 参数曲面的 连续性
连续性
定义11.4两参数曲面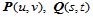 沿它们的正则公共连接线
沿它们的正则公共连接线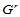 连续,当且仅当其中之一比如
连续,当且仅当其中之一比如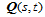 可被重新参数化为
可被重新参数化为 ,使得它们沿该公共连接线
,使得它们沿该公共连接线 连续,即:
连续,即:
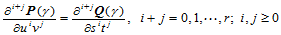
也可以定义为下述形式:
两参数曲面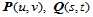 沿正则公共连接线
沿正则公共连接线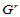 连续的,如果存在
连续的,如果存在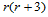 个形状函数满足Beta约束:
个形状函数满足Beta约束:
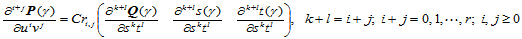
这里,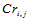 表示Beta约束的矢值函数,它是后面括号内的那么偏导矢与标量函数的矢量函数,而标量函数称为形状函数。
表示Beta约束的矢值函数,它是后面括号内的那么偏导矢与标量函数的矢量函数,而标量函数称为形状函数。
具有
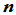 面角点的Bézier曲面片的
面角点的Bézier曲面片的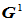 拼接
拼接
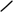
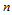 张曲面交汇于一点,互相又由曲面片的边界线连接在一起,这
张曲面交汇于一点,互相又由曲面片的边界线连接在一起,这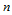 张曲面片上的公共角点称之为
张曲面片上的公共角点称之为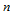 面角点。它们的定义域构成一非矩形网格,例如图11.1所示的曲面,分别有三角点、四面角点和五面角点。这里遇到的问题是:这些曲面片除相邻间要求光滑连接外,还要求在公共的
面角点。它们的定义域构成一非矩形网格,例如图11.1所示的曲面,分别有三角点、四面角点和五面角点。这里遇到的问题是:这些曲面片除相邻间要求光滑连接外,还要求在公共的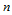 面角点处实现光滑拼接。与两曲面片间的光滑连接不同之处在于,这里的连续性条件相互缠绕
面角点处实现光滑拼接。与两曲面片间的光滑连接不同之处在于,这里的连续性条件相互缠绕 在一起。
在一起。 面角点具有奇偶性,依据交汇于该角点的曲面片数或边界线数是奇数或偶数,而称之为奇数角点或偶数角点。
面角点具有奇偶性,依据交汇于该角点的曲面片数或边界线数是奇数或偶数,而称之为奇数角点或偶数角点。

下面,我们讨论这一问题。为方便起见,假设有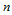 张
张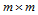 次Bézier曲面片:
次Bézier曲面片:
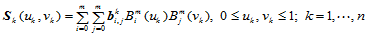 (11.11.1)
(11.11.1)
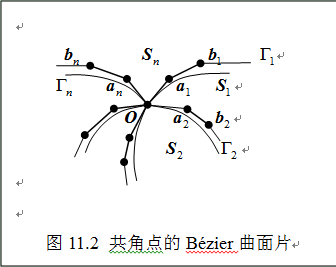
交汇于公共角点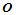 处,如图11.2所示。这些曲面片的边界曲线按围绕
处,如图11.2所示。这些曲面片的边界曲线按围绕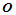 顺时针循环编号为
顺时针循环编号为 ,每顺序相邻的两曲面片沿公共边界曲线
,每顺序相邻的两曲面片沿公共边界曲线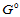 连续,进而假定每条边界曲线
连续,进而假定每条边界曲线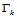 的取向都是由角点
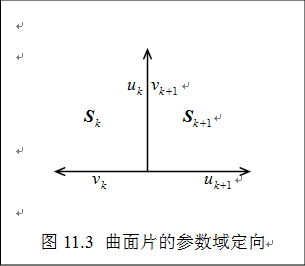
的取向都是由角点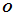 出发朝向外部,即曲面片的参数域定向如图11.3所示。曲面片
出发朝向外部,即曲面片的参数域定向如图11.3所示。曲面片 和
和 的公共边界曲线是:
的公共边界曲线是:
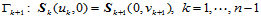 (11.11.2)
(11.11.2)
这里,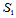 和
和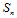 具有公共边界曲线:
具有公共边界曲线:

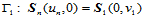 (11.11.3)
(11.11.3)
根据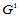 连续性条件,存在常数
连续性条件,存在常数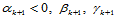 ,使得:
,使得:
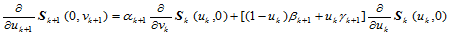 (11.11.4)
(11.11.4)
即:
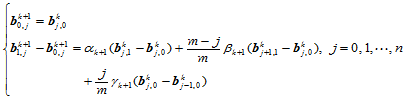 (11.11.5)
(11.11.5)
为了讨论简单起见,我们重新标记公共角点 处邻近的控制顶点如下:
处邻近的控制顶点如下:


即边界曲线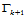 上与角点
上与角点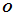 顺序相接的两个控制顶点,及以
顺序相接的两个控制顶点,及以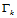 和
和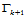 为边界曲线的曲面片
为边界曲线的曲面片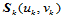 最接近角点
最接近角点 的内控制顶点。这样,如果沿每条边界曲线
的内控制顶点。这样,如果沿每条边界曲线 的
的 条件得到满足,那么围绕
条件得到满足,那么围绕 面角点
面角点 的
的 张曲面片便达到
张曲面片便达到 连续了。根据每条边界上的
连续了。根据每条边界上的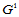 连续性条件,便可得到围绕角点
连续性条件,便可得到围绕角点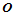 的全部
的全部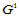 连续性条件。这些条件分为两组:
连续性条件。这些条件分为两组:
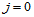 时得到第一组约束方程(从
时得到第一组约束方程(从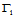 到
到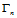 ):
):
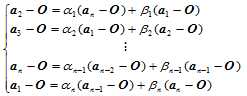 (11.11.6)
(11.11.6)
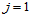 时得到第二组约束方程:
时得到第二组约束方程:
 (11.11.7)
(11.11.7)
为满足这两组约束方程,所涉及的顶点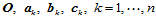 必须以相容的方式定义。我们首先选定角点
必须以相容的方式定义。我们首先选定角点 ,然后由方程(11.11.6)确定顶点
,然后由方程(11.11.6)确定顶点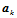 ,最后由方程(11.11.7)确定顶点
,最后由方程(11.11.7)确定顶点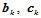 。
。
考察方程(11.11.6)可以发现,每个方程都表示了顺序三个顶点 必须与角点
必须与角点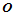 共面。由此可得,
共面。由此可得, 个顶点
个顶点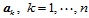 必须和角点
必须和角点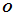 共面,该平面即为曲面片在角点
共面,该平面即为曲面片在角点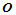 处的切平面,设其法矢为
处的切平面,设其法矢为 。此外,每个约束方程左端都包含在下个约束方程右端第二项之中。因此,第
。此外,每个约束方程左端都包含在下个约束方程右端第二项之中。因此,第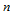 个约束方程和第一个约束方程右端都可写成矢量
个约束方程和第一个约束方程右端都可写成矢量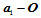 与
与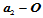 的线性组合:
的线性组合:
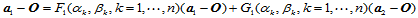
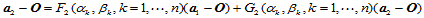
其中, ,都是以
,都是以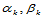 为变量的多项式函数,这些变量的次数不超过1。当然,可以任意选择两个顺序的顶点
为变量的多项式函数,这些变量的次数不超过1。当然,可以任意选择两个顺序的顶点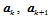 来替代上式中的
来替代上式中的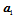 与
与 。
。
现在,在过点 ,以
,以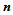 为法矢的切平面内选择与
为法矢的切平面内选择与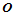 不共线的两个点
不共线的两个点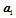 、
、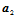 。这等价于:
。这等价于:

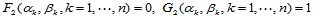
将式(11.11.6)中第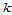 个方程两端叉乘
个方程两端叉乘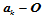 后再点乘
后再点乘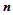 ,得到:
,得到:
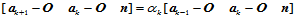
于是
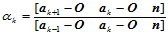
类似地

 的几何意义是三角形
的几何意义是三角形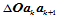 面积与三角形
面积与三角形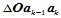 面积之比,从而有:
面积之比,从而有:
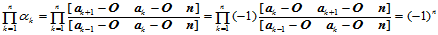 (11.11.8)
(11.11.8)
这便是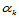 的约束条件。可根据需要选择
的约束条件。可根据需要选择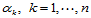 使之满足上式,然后再根据需要选定
使之满足上式,然后再根据需要选定 个
个 ,剩下的三个
,剩下的三个 由约束方程确定。
由约束方程确定。
下面,我们进一步确定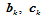 。为了使连续性约束尽可能少地传播,我们首先根据需要选定顶点
。为了使连续性约束尽可能少地传播,我们首先根据需要选定顶点 ,然后再由约束方程(11.11.7)确定
,然后再由约束方程(11.11.7)确定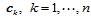 。将约束方程(11.11.7)改写成矩阵形式:
。将约束方程(11.11.7)改写成矩阵形式:
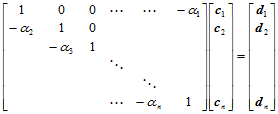 (11.11.9)
(11.11.9)
其中,  。
。
方程组(11.11.9)的系数矩阵为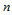 阶方阵,其行列式的值是:
阶方阵,其行列式的值是:
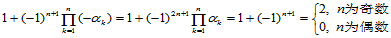 (11.11.10)
(11.11.10)
因此, 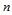 为奇数,即
为奇数,即 面角点为奇角点时,方程组(11.11.9)有惟一解。当
面角点为奇角点时,方程组(11.11.9)有惟一解。当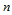 为偶数,即
为偶数,即 面角点为偶角点时,由方程组(11.11.9)不能惟一定解。由于此时系数矩阵的秩为
面角点为偶角点时,由方程组(11.11.9)不能惟一定解。由于此时系数矩阵的秩为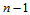 ,因而解的存在性等价于增广矩阵与系数矩阵同秩。这意味着矢量
,因而解的存在性等价于增广矩阵与系数矩阵同秩。这意味着矢量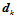 必须满足约束条件:
必须满足约束条件:
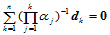 (11.11.11)
(11.11.11)
当该补充约束条件成立时,将其代入 的表达式中,改写方程组(11.11.9),即可求出
的表达式中,改写方程组(11.11.9),即可求出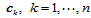 。
。
与奇数角点相比,在偶数角点处,顶点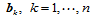 ,不能任意确定,这便增加了确定控制顶点的难度。
,不能任意确定,这便增加了确定控制顶点的难度。
当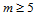 时,我们可以仅仅在控制顶点
时,我们可以仅仅在控制顶点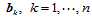 ,的选择上增加一线性约束,而不影响局部确定其他共面角点邻近的控制顶点。当
,的选择上增加一线性约束,而不影响局部确定其他共面角点邻近的控制顶点。当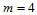 时,若
时,若 为奇数,仍可以局部确定控制顶点,但是若至少有一边界的另一端为偶数角点时,所有这些约束便缠绕在一起,使得控制顶点的局部确定不再可能。当
为奇数,仍可以局部确定控制顶点,但是若至少有一边界的另一端为偶数角点时,所有这些约束便缠绕在一起,使得控制顶点的局部确定不再可能。当 时,控制顶点的确定必须只整体的。
时,控制顶点的确定必须只整体的。
以上的讨论都是在非零的 和
和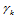 情况下进行的。正是由于非零的
情况下进行的。正是由于非零的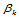 和
和 的存在,才引起约束的传播。若分片曲面定义在矩形网格上时,我们可以在每个四角点处置
的存在,才引起约束的传播。若分片曲面定义在矩形网格上时,我们可以在每个四角点处置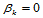 、
、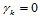 。这种特殊的选择使得顶点
。这种特殊的选择使得顶点 不在约束中出现,当由方程组(11.11.6)求出
不在约束中出现,当由方程组(11.11.6)求出 后,约束方程组(11.11.7)自动满足。因而,在这种特殊情况下围绕每个四角点局部确定控制顶点得以保持。这样,采用双三次曲面也就够了。然而,对于非四角点,取
后,约束方程组(11.11.7)自动满足。因而,在这种特殊情况下围绕每个四角点局部确定控制顶点得以保持。这样,采用双三次曲面也就够了。然而,对于非四角点,取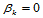 、
、 不再可能,否则将引起退化曲面片的退化。此时,为了保证围绕每个角点获得控制顶点的局部确定,可采用双五Bézier次曲面,它为限制围绕偶数角点的
不再可能,否则将引起退化曲面片的退化。此时,为了保证围绕每个角点获得控制顶点的局部确定,可采用双五Bézier次曲面,它为限制围绕偶数角点的 连续性约束的传播提供了充分的自由度。
连续性约束的传播提供了充分的自由度。




