第十一章 Bézier曲面
在第十章,我们利用直积(张量积)的方法,把参数三次曲线扩展成参数双三次曲面。本章仍然运用这一思想,将Bézier曲线拓广成Bézier曲面。
11.1 Bézier曲面的定义及性质
给定三维空间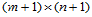 个点
个点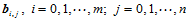 ,
,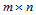 次参数曲面:
次参数曲面:
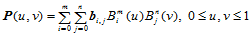 (11.1.1)
(11.1.1)
称为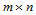 次Bézier曲面,式中
次Bézier曲面,式中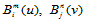 分别是
分别是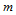 次Bernstein基函数和
次Bernstein基函数和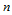 次Bernstein基函数。
次Bernstein基函数。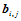 称为曲面片的控制顶点或Bézier点,逐次用线段连接点列
称为曲面片的控制顶点或Bézier点,逐次用线段连接点列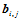 中相邻两点组成的空间网格叫做曲面片的控制网格或Bézier网格。
中相邻两点组成的空间网格叫做曲面片的控制网格或Bézier网格。
Bézier曲面是通过用张量积方法将一元Bernstein基推广为二元Bernstein基,来实现由Bézier曲线向Bézier曲面的推广。因此,Bézier曲线的许多性质在Bézier曲面场合下同样成立,具体有以下几条:
1. 仿射不变性;
2. 凸包性;
3. 边界性质。Bézier曲面的四条边界曲线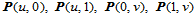 分别是
分别是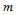 次和
次和 次Bézier曲线,且四个控制角点
次Bézier曲线,且四个控制角点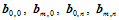 位于曲面之上;
位于曲面之上;
4. 等参数线。固定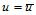 ,那么曲线
,那么曲线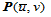 是一条
是一条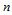 次Bézier曲线,其控制顶点为
次Bézier曲线,其控制顶点为
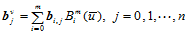
同理,固定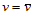 ,其参数曲线
,其参数曲线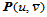 为一条
为一条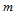 次Bézier曲线,相应的控制顶点为
次Bézier曲线,相应的控制顶点为
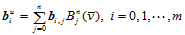
然而变差缩减性对Bézier曲面将不再成立。
11.2 低次Bézier曲面
实际工程应用中,曲面片的次数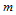 和
和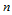 通常不宜过高,以不超过5次为宜。否则,Bézier网格对曲面的控制能力将会大为减弱。当然,最为重要的Bézier曲面是
通常不宜过高,以不超过5次为宜。否则,Bézier网格对曲面的控制能力将会大为减弱。当然,最为重要的Bézier曲面是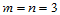 的情形,即双三次Bézier曲面片。下面,我们先考虑两类低次曲面,然后专门讨论双三次Bézier曲面片。
的情形,即双三次Bézier曲面片。下面,我们先考虑两类低次曲面,然后专门讨论双三次Bézier曲面片。
11.2.1 双一次Bézier曲面
双一次Bézier曲面是双线性插值曲面,通过四个Bézier点,每条边界曲线都是直线段,而且任一等参数线也都是直线段。因此,它是一直纹面,其几何分类就是双曲抛物面(马鞍面)。
双一次Bézier曲面的方程是:
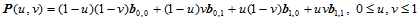 (11.2.1)
(11.2.1)
为了证明双一次Bézier曲面是抛物面,我们将曲面片的方程改写为:
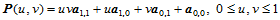 (11.2.2)
(11.2.2)
这里,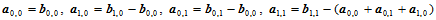 。
。
记曲面上的点 为
为
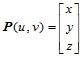
那么

当四点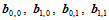 共面时,由Bézier曲面的凸包性质可知,双一次Bézier曲面为一平面片。否则,三向量
共面时,由Bézier曲面的凸包性质可知,双一次Bézier曲面为一平面片。否则,三向量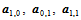 不共面,因此矩阵
不共面,因此矩阵 可逆。此时有
可逆。此时有
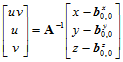
对曲面片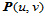 做仿射坐标变换:
做仿射坐标变换:
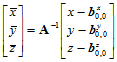
那么,在新的仿射坐标系下,双一次Bézier曲面片上任一点的仿射坐标满足方程:
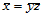
这就是双曲抛物面只方程。
11.2.2 双二次Bézier曲面
对于双二次Bézier曲面片
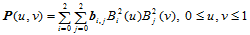
来说,其边界曲线和参数坐标曲线均为抛物线。九个Bézier点所组成的控制网格的周围八个顶点决定了曲面片的四条边界曲线,内Bézier点 仅影响曲面内部形状,对边界曲线不产生影响。
仅影响曲面内部形状,对边界曲线不产生影响。
从Bézier曲面片对Bézier网格的逼近性可知,在固定四条边界线以后,通过顶点 之选择,便可使曲面或凸或凹、或臌或瘪。
之选择,便可使曲面或凸或凹、或臌或瘪。
11.2.3 双三次Bézier曲面
双三次Bézier曲面片是工程设计中最为常用的曲面类型,其矩阵表示如下:
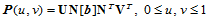 (11.2.3)
(11.2.3)
式中, ,
,
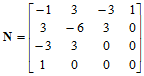
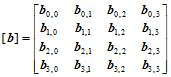
这样以来,对于同一张双三次参数曲面而言,我们有两种表示形式:Bézier形式和Hermite形式,即:
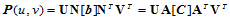
从而得到双三次Bézier曲面在四个角点处的几何信息:

因此,有
 (11.2.5)
(11.2.5)
由此可以看出,混合偏导矢反映了内Bézier点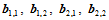 相对于角点曲面片切平面的扭曲状况,因此角点处的混合偏导矢亦称做"扭矢"(twist)。在Ferguson样条曲面中,假定扭矢为零,即就是内Bézier点分别位于对应角点处的切平面上。
相对于角点曲面片切平面的扭曲状况,因此角点处的混合偏导矢亦称做"扭矢"(twist)。在Ferguson样条曲面中,假定扭矢为零,即就是内Bézier点分别位于对应角点处的切平面上。
11.3 de Casteljau算法
类似于Bézier曲线上点的计算,Bézier曲面上的点的计算亦可由一系列线性插值来完成,对应的算法称之为de Casteljau算法。
对于给定的Bézier曲面
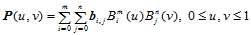
参数为 的点
的点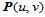 可计算如下:
可计算如下:
1.
 (11.3.1)
(11.3.1)
或
2.
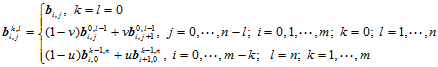 (11.3.2)
(11.3.2)
按算法1进行时,先以参数值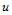 对控制网格沿
对控制网格沿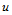 向的
向的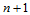 个多边形执行曲线的de Casteljau算法,
个多边形执行曲线的de Casteljau算法,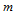 级递推后,得到沿
级递推后,得到沿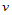 向的由
向的由 个顶点
个顶点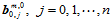 构成的中间多边形。再以参数
构成的中间多边形。再以参数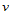 对其执行曲线的de Casteljau算法,
对其执行曲线的de Casteljau算法,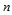 级递推后,得到曲面上对应的点
级递推后,得到曲面上对应的点 。按算法2进行时,先以参数值
。按算法2进行时,先以参数值 对控制网格沿
对控制网格沿 向的
向的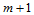 个多边形执行曲线的de Casteljau算法,
个多边形执行曲线的de Casteljau算法,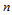 级递推后,得到沿
级递推后,得到沿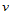 向的由
向的由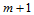 个顶点
个顶点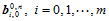 构成的中间多边形。再以参数
构成的中间多边形。再以参数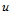 对其执行曲线的de Casteljau算法,
对其执行曲线的de Casteljau算法,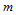 级递推后,同样得到曲面上对应的点
级递推后,同样得到曲面上对应的点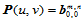 。
。
特别,当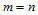 时,上述两个算法中的单参数线性插值可合并成双参数线性插值。
时,上述两个算法中的单参数线性插值可合并成双参数线性插值。
3.
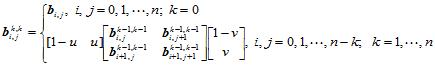 (11.3.3)
(11.3.3)
算法3利用了参数平面上单位正方形区域到控制网格的每个子四边形的仿射参数变换,确定参数域上点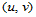 对应的诸中间点,执行
对应的诸中间点,执行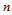 级双线性插值递推后,得到所求的点
级双线性插值递推后,得到所求的点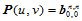 。
。
对于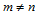 的情况,算法3不能进行到底。在执行
的情况,算法3不能进行到底。在执行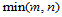 级双线性插值递推后,得到由
级双线性插值递推后,得到由 个顶点构成的一个中间多边形。然后,以该多边形方向的参数值对该多边形执行单参数线性插值递推,直到最后得到一个点
个顶点构成的一个中间多边形。然后,以该多边形方向的参数值对该多边形执行单参数线性插值递推,直到最后得到一个点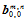 即为所求曲面上的点。
即为所求曲面上的点。
当然,上述算法中的任一种所得结果完全相同,其时间复杂度亦完全一样。基于de Casteljau算法编制的程序稳定可靠、直观简便、快速。由于Bézier曲面是Bézier曲线的直接推广,其曲面的计算化解为一系列曲线的计算。基于这一点,采用单参数线性插值方案可直接调用曲线计算的程序,避免了用双线性插值方案重复编程的麻烦。
11.4 Bézier曲面的分割
计算Bézier曲面上点的de Casteljau算法之直接应用之一,就是Bézier曲面的分割。给定参数点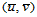 ,那么参数平面
,那么参数平面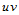 上的定义域被其分割成四个子矩形区域
上的定义域被其分割成四个子矩形区域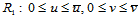 ,
,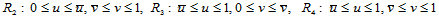 。与此相对应的曲面上的点
。与此相对应的曲面上的点 及等参数线
及等参数线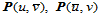 一起亦将曲面分割成四块,每一块都是
一起亦将曲面分割成四块,每一块都是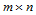 次Bézier曲面,因而可表示成Bézier形式,相应的控制顶点就是计算点
次Bézier曲面,因而可表示成Bézier形式,相应的控制顶点就是计算点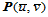 时,de Casteljau算法产生的一系列中间点,即:
时,de Casteljau算法产生的一系列中间点,即:
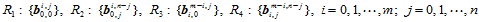 (11.4.1)
(11.4.1)
事实上,中间点 有以下显式表示:
有以下显式表示:
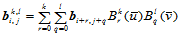 (11.4.2)
(11.4.2)
那么,定义在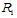 上的由控制顶点
上的由控制顶点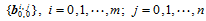 确定
确定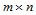 次Bézier曲面片为:
次Bézier曲面片为:
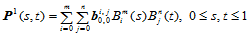
由于
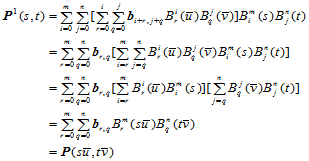
因此,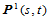 即为曲面
即为曲面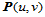 在
在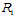 上的那一部分。
上的那一部分。
11.5 Bézier曲面的升阶
Bézier曲面的升阶同样也是Bézier曲线升阶的推广。如果我们把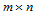 次Bézier曲面改写为
次Bézier曲面改写为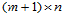 次曲面,即使:
次曲面,即使:
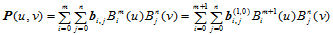 (11.5.1)
(11.5.1)
那么,新的控制顶点可确定如下:
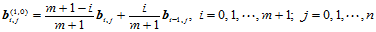 (11.5.2)
(11.5.2)
同样,也可沿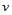 向进行升阶,即:
向进行升阶,即:
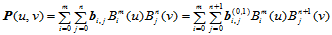 (11.5.3)
(11.5.3)
则新的控制顶点为:
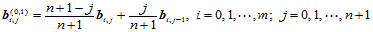 (11.5.4)
(11.5.4)
如果沿两个参数方向同时对曲面升阶一次,即:
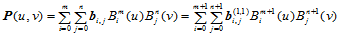 (11.5.5)
(11.5.5)
则新的控制顶点为:
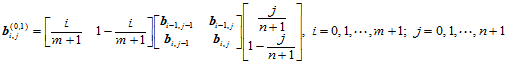 (11.5.6)
(11.5.6)
对于Bézier曲面的升阶可无限进行下去,便可得到一系列开展多面体,它们都定义同一张曲面片。假设将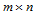 次Bézier曲面
次Bézier曲面 次Bézier曲面,即:
次Bézier曲面,即:
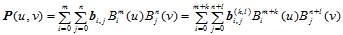
则新的控制顶点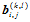 可递推计算如下:
可递推计算如下:
1. 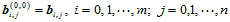
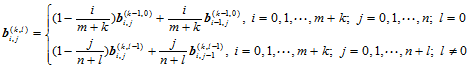 (11.5.7)
(11.5.7)
或者
2. 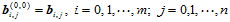
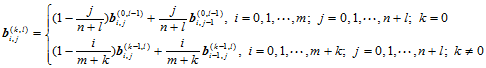 (11.5.8)
(11.5.8)
或者
3. 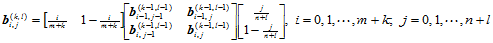 (11.5.9)
(11.5.9)
11.6 Bézier曲面的偏导矢与法矢
Bézier曲面的偏导矢计算是Bézier曲线导矢计算之推广,相应地有以下计算公式:
- 单向导矢:
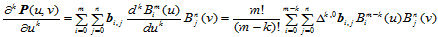 (11.6.1)
(11.6.1)
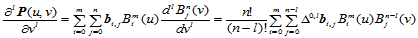 (11.6.2)
(11.6.2)
其中,向前差分矢量定义如下:
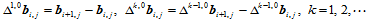
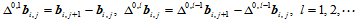
当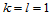 时,分别得到
时,分别得到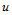 向参数线的切矢和
向参数线的切矢和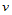 向参数线的切矢。
向参数线的切矢。
- 混合偏导矢
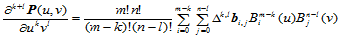 (11.6.3)
(11.6.3)
这里,向前差分为:
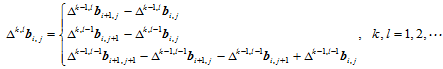
由于曲面的偏导矢本身是一Bézier曲面,因此利用de Casteljau算法即可得到如下的偏导矢计算公式:
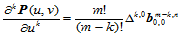 (11.6.4)
(11.6.4)
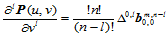 (11.6.5)
(11.6.5)
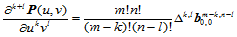 (11.6.6)
(11.6.6)
这表明,Bézier曲面的偏导矢可作为Bézier曲面的de Casteljau算法的"副产品"同时求出来。
- 法矢
曲面在一点的法矢由该点处的两参数线的切矢所决定,因而法矢的计算公式为:
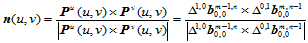 (11.6.7)
(11.6.7)
特别,在曲面片四个角点处的法矢可简单地予以计算如下:


11.7 非参数Bézier曲面
设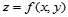 为一二元Bernstein多项式
为一二元Bernstein多项式
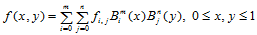
其图形是一曲面。如果我们将其看成是一Bézier曲面,那么定义此曲面的Bézier点是什么?为此,我们将 改写成参数形式
改写成参数形式
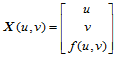
由于Bernstein基函数具有多项式精度,所以
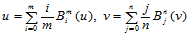
因此
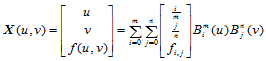
故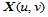 的Bézier点是:
的Bézier点是:
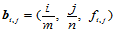
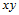 平面上的点
平面上的点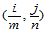 称为函数
称为函数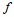 的Bézier横标,而
的Bézier横标,而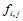 则称为Bézier纵标。
则称为Bézier纵标。
当然,二元Bernstein多项式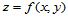 的定义域并不要求一定是
的定义域并不要求一定是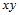 平面上的单位正方形区域,其实
平面上的单位正方形区域,其实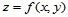 的定义域只要是一平行四边形区域即可,例如,若定义域由点
的定义域只要是一平行四边形区域即可,例如,若定义域由点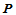 和两个向量
和两个向量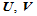 给出,那么其Bézier横标就是:
给出,那么其Bézier横标就是:

特别,对于二元Bernstein多项式来说,有以下结果:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号