第十章 参数双三次样条曲面
10.1 曲面设计技术概述
利用前面所讲的各种曲线设计方法,我们就可以建立起产品外形的线框模型。众所周知,设计人员在构思一个产品的形状时,通常用线条勾画出一个用轮廓线表示的立体图,以帮助构思和相互讨论。若用计算机来实现这一构图过程,就是建立产品的线框模型。
线框模型(Wireframe)是由有限个空间点以及成对点之间相连的边(直边或曲边)构成的三维几何模型,计算机不仅可用来构造线框模型,而且还能快速而准确地生成所需要的各种正投影图、轴侧图和任意视线方向的透视投影图。线框模型具有很多优点。首先,它的定义过程最简单,符合长期以来工程技术人员的打样习惯。人们在设计构思时,总是先用线条勾画出形体的基本轮廓,然后逐步细化;其次,它的数据存储量最小、操作灵活、响应速度快。事实上,灵活方便的线框功能有时是进一步构造表面模型和实体模型的工具,是交互式CAD系统中改善用户界面的有力手段,是从三维模型产生各种二维视图和工程图的最简捷途径。因此,线框模型是基本的普遍采用的一种三维几何模型。
但是,由于线框模型过于简单,不包含面的信息,因而有时不能惟一定义物体的形状,甚至定义出实际不可能存在的形体;不能自动消除隐藏线;无法计算物体的体积;无法进行产品的力学性能分析、生成加工指令等等。那么,为了用计算机进行复杂产品的外形的表示和设计就必须引入曲面方法来描述它们。
10.1.1 曲面模型
三维几何形体的曲面模型是在线框模型的基础上增加面的信息,相当于在灯笼骨架外蒙上一张皮。曲面不一定封闭,正如灯笼的上下两端可以留出开口一样。曲面模型是比线框模型更完全、二义性更小的数学表示方法,它为形体提供了更多的几何信息。利用曲面模型,可以生成数控加工刀具轨迹、进行物性计算;可以在程序中实现隐藏线的自动消除、生成产品的真实感图形;也可以在有限元分析中生成表面的有限元网格。曲面模型通过提供连接物体边界的曲面间的拓扑信息而超越了线框模型。
在曲面模型中,主要研究具有一定光滑性的曲面外形的数学描述,其历史由来已久。早在计算机问世以前,人们在船舶外形设计中就使用放样方法(lofting)进行曲面外形设计 。然而,CAD/CAM中曲面表示方法的研究和发展则始于S. Coos、P. Bézier和de Casteljau的开创性工作,他们分别对立地提出了现在称之为Coos曲面和Bézier曲面的曲面设计方法。曲面表示方法是CAD/CAM中最为关键的恶疾书之一,这是因为三维物体的外形都是曲面构成的,它是物体和周围环境之间的界面,物体对光照的反射、物体的光色效应取决于物体外形的形状、颜色和纹理材料的性质等等。三维形体的几何表示处处需要曲面,从大到飞机、船舶、汽车,小到家用电器、轻工产品的工业造型设计,服装、皮鞋的三维打样、款式设计,山脉、水浪、云彩等自然景观的模拟等等无不需要强有力的曲面造型工具。有关曲面造型的方法很多,目前仍是CAD/CAM领域中最活跃的方向之一。没有解决所有问题的统一方法,例如在工业产品外形设计中,广泛采用的是矩形拓扑结构上的曲面方法,象Bézier曲面、B样条曲面、NURBS曲面等。而在实验数据处理、地形图、有限元的前置处理等方面,则采用的是任意拓扑结构上的曲面方法,如三角Bézier曲面、Shepard曲面等。
总之,在CAD/CAM领域中,常用的曲面表示方法有以下几类:
- Coos曲面和Bézier曲面;
- 张量积曲面;
- 三角曲面;
- 离散曲面。
10.1.2 曲面造型的要求
一般来说,构造曲面要求两方面的信息:① 定量数据,如点、切矢等;② 定性数据,象光滑性、视觉美观性等。定量数据和定性数据亦分别称为构造曲面的"硬"数据和"软"数据,曲面的表示形式必须能够给设计者提供一个简单、易于交互处理的形式,以便能灵活地使用这两类数据。与曲线的表示类似,曲面方法也应该具有能够插值或逼近给定"硬"数据的品质。至于定性数据,则不免带有浓厚的主观色彩,不同的设计者具有不同的审美观,但最终产生的形体都异曲同工、差别不大。这表明定性数据还具有客观性的一面,把这一方面抽象出来,用数学的方法加以量化描述,便得到构造曲面所遵循的定性准则──光顺准则。
10.1.3 高维曲面
除了表示和设计产品的几何外形之外,通常也要求曲面方法能够用于处理实验数据、列表数据、测量数据以及微分方程的离散解等等,在这种情况下就引出了高维曲面,也就是给定三维空间的位置点和每点处的某种变量之值,如何构造表示这种变量分布的曲面。例如飞机机翼上的压力分布曲面、机械零件上的应力分布曲面、地矿中采矿采凿面上的位移分布曲面等。这类四维曲面的构造通常分两步完成:① 求变量分布的等值线;② 以彩色编码的形式显示。高维曲面是可视化计算的主要工具。
10.1.4 曲面表示形式的选取
曲面形式的选取依赖于具体的应用,没有解决所有问题的统一方法,比如用于构造汽车车身的曲面方法就不适合于人体心脏的模拟。此外,曲面形式的选择也依赖于加工曲面的加工方法,通常人们喜欢选择便于三坐标数控机床加工的曲面形式,而不是五坐标数控机床加工的曲面形式,这样可降低加工费用。然而无论做何种选择,所有的曲面表示形式都必须以易于求微分、以便确定曲面的切矢、法矢和曲率等几何量为前提,因此最自然的选择是多项式函数。从曲面设计的观点看,选择高阶多项式是不合适的,这是因为大量的系数使得难以控制曲面的形状、或导致曲面出现不期望的震荡而影响曲面的品质。所以,就大多数实际应用而言,选取三次多元多项式已足够了。当然,如果可能也希望选择的曲面表示形式既适合曲面表示,也适合曲面设计。这里所谓曲面表示是指形体的计算机表示,即用给定的数据在计算机内表示和处理所定义的曲面。曲面表示可以是三维的、也可以是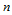 维空间的物体。而曲面设计则指的是用给定的关键数据通过交互方式获得要求的曲面外形,它通常是在三维空间进行的。
维空间的物体。而曲面设计则指的是用给定的关键数据通过交互方式获得要求的曲面外形,它通常是在三维空间进行的。
10.1.5 曲面的描述
最直接、最简单的描述曲面的方法是列出曲面上的所有点。这种方法最为笨拙,用它不可能导出任何曲面性质。因此,通常仅用曲面上很有限的点列,借助于插值或逼近技术来生成曲面的表示形式,当然,最完美的方法是知道曲面的解析方程。当解析方程不合适时,则将曲面看成是由一系列小曲面依照一定光滑性条件缝合而成。
10.1.6 曲面造型方法及显示
曲面造型方法分为两大类:一是以曲线为基础,即由曲线构造曲面。例如给定两条边界曲线,可构造一张直纹面;给定一母线和旋转轴可构造一旋转面等。二是以离散点集为基础,即由点直接构造曲面,象插值、逼近、拟合等。
曲面的显示通过曲面上的网格线来实现,也就是说,计算出曲面上的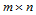 个点,按一定的顺序(等参数线)连接成网格线显示,其网格单元的大小由用户确定。
个点,按一定的顺序(等参数线)连接成网格线显示,其网格单元的大小由用户确定。
10.2 双三次样条函数
10.2.1 双三次样条函数的定义
给定空间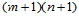 个数据点
个数据点
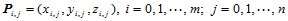
我们来构造插值于这些数据点的一张曲面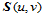 。
。
众所周知,曲线是一元函数,曲面是二元函数。在讨论插值曲线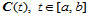 时,我们采用的方法是给定自变量区间
时,我们采用的方法是给定自变量区间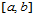 一个分割:
一个分割: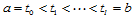 ,在每个子区间上构造一三次多项式,使得
,在每个子区间上构造一三次多项式,使得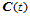 在
在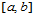 上
上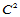 连续,且在每一个分割点上
连续,且在每一个分割点上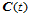 满足给定的插值条件。为了在曲面情况下使用这种方法,即把一元三次样条函数的概念推广到二元场合,就需要在以下两方面进行推广:
满足给定的插值条件。为了在曲面情况下使用这种方法,即把一元三次样条函数的概念推广到二元场合,就需要在以下两方面进行推广:
- 定义域及其分割;
- 构造样条函数类及连接的连续性。
最简单且一目了然的一种构造方法是:
⑴ 采用矩形定义域和矩形网格线的分割,即采用两个一维分割的张量积,具体如下:
设曲面片的定义域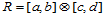 是参数
是参数 平面上的矩形区域,在
平面上的矩形区域,在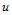 轴和
轴和 轴上分别取其分割:
轴上分别取其分割:
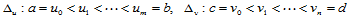
由此可导出 的一个矩形网格分割
的一个矩形网格分割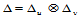 ,将
,将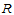 分割成
分割成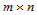 个子矩形
个子矩形

其两条邻边的长分别是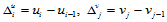 。直线
。直线 和
和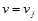 称为分割
称为分割 的两族网格线,网格线的交点
的两族网格线,网格线的交点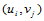 称为
称为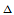 的节点。
的节点。
⑵
采用双三次多项式作为构造样条的函数类,就是用两个一元三次多项式的张量积。具体说,凡在 上满足下述条件的二元函数
上满足下述条件的二元函数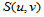 称为双三次插值样条函数:
称为双三次插值样条函数:
①
在每个子区域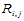 上,
上,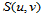 关于参数
关于参数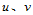 都是三次多项式,即:
都是三次多项式,即:
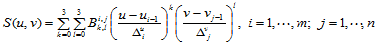 (10.2.1)
(10.2.1)
②
在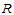 上,函数
上,函数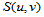 的偏导数
的偏导数
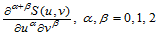
是连续的,简记为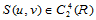 。
。
③ 给定一组数列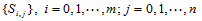 ,
, 满足条件
满足条件
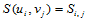 (10.2.2)
(10.2.2)
这里,二阶偏导数连续的要求用以保证二元样条函数所张成的曲面具有连续的Gauss曲率和平均曲率,相当于一元场合下对曲线的曲率连续的要求。
10.2.2 双三次插值样条函数的确定
1. 双三次样条函数的表示
我们知道在 轴上关于分割
轴上关于分割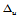 的三次样条函数的全体构成一
的三次样条函数的全体构成一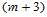 维的线性空间
维的线性空间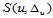 ,同理在
,同理在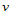 轴上关于分割
轴上关于分割 的三次样条函数的全体亦构成一
的三次样条函数的全体亦构成一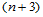 的线性空间
的线性空间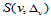 。
。
在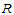 给定分割
给定分割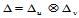 后所定义的双三次样条函数的全体构成一个线性空间
后所定义的双三次样条函数的全体构成一个线性空间 ,由于双三次样条函数是两个一元三次样条函数的直积,即:
,由于双三次样条函数是两个一元三次样条函数的直积,即:
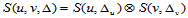
所以,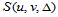 是
是 维线性空间。
维线性空间。
对于线性空间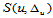 来说,它的基样条
来说,它的基样条 满足以下条件:
满足以下条件:
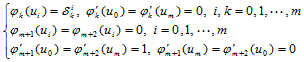
同理,线性空间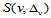 的基样条
的基样条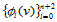 满足以下条件:
满足以下条件:

而两个一元三次基样条的直积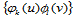 恰好构成线性空间
恰好构成线性空间 的一组基底,这样一来
的一组基底,这样一来 中任意一个双三次样条函数都具有以下表示形式:
中任意一个双三次样条函数都具有以下表示形式:
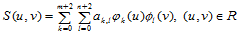
 (10.2.3)
(10.2.3)
2. 边界条件
对于双三次插值样条函数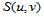 来说,它的表达式中有
来说,它的表达式中有 个待定系数
个待定系数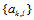 ,而插值条件
,而插值条件 仅有
仅有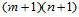 ,因此尚剩余
,因此尚剩余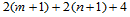 个自由度,而这些则通过边界条件来决定。最常用的一种边界条件是给定以下数值:
个自由度,而这些则通过边界条件来决定。最常用的一种边界条件是给定以下数值:
①
矩形 的四条边界上的所有节点处的一阶法向偏导数:
的四条边界上的所有节点处的一阶法向偏导数:
 (10.2.4)
(10.2.4)
②
矩形 的四个角点处的二阶混合偏导数
的四个角点处的二阶混合偏导数
 (10.2.5)
(10.2.5)
3. 存在唯一性定理
定理10.1 给定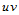 平面上的矩形区域
平面上的矩形区域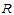 ,它的一个矩形分割
,它的一个矩形分割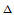 和
和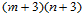 个常数:
个常数:
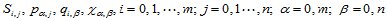
则存在惟一的一个双三次插值样函数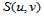 ,使其满足插值条件和边界条件:
,使其满足插值条件和边界条件:
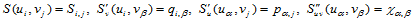
证明 在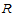 上关于给定分割
上关于给定分割 的任意一个双三次样条函数
的任意一个双三次样条函数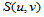 都具有基样条表示式
都具有基样条表示式
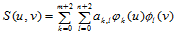
根据基样条的性质及插值条件,有:

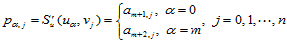

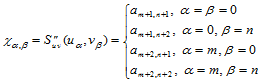
上述各式的右端无重复地出现了每一个未知量,而偏导数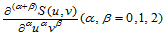 的连续性则由每一个基样条的
的连续性则由每一个基样条的 连续性得到保证。
连续性得到保证。
4. 三次插值样条函数的求解
当我们应用定理10.1到单个矩形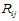 时,只要给定
时,只要给定 的四个角点上的函数值,两个方向的一阶偏导数以及二阶混合偏导数这十六个数据,也就是给定四阶方阵
的四个角点上的函数值,两个方向的一阶偏导数以及二阶混合偏导数这十六个数据,也就是给定四阶方阵
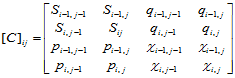 (10.2.6)
(10.2.6)
那么,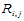 上的双三次函数
上的双三次函数 就被惟一地决定了。矩阵
就被惟一地决定了。矩阵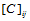 中各元素的定义分别是:
中各元素的定义分别是:

显然,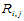 上的双三次函数可以写成以下的形式
上的双三次函数可以写成以下的形式
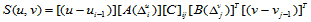 (10.2.7)
(10.2.7)
其中:

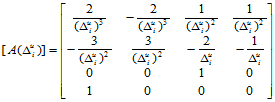
这样一来,双三次样条函数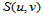 在子区域
在子区域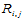 上的表示式完全取决于矩阵
上的表示式完全取决于矩阵 ,
, 的左上角的四个元素由插值条件直接给出,其余的十二个元素则需按照边界条件,通过求解连续性方程来求得。
的左上角的四个元素由插值条件直接给出,其余的十二个元素则需按照边界条件,通过求解连续性方程来求得。
首先,固定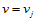 ,则函数
,则函数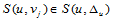 ,那么其
,那么其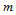 连续性方程为
连续性方程为
 (10.2.8)
(10.2.8)
其中,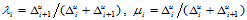 。
。
利用边界条件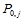 和
和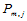 可由上述方程组求出
可由上述方程组求出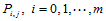 ,从而求出
,从而求出 上所有节点
上所有节点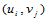 处的沿
处的沿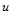 向的一阶偏导数
向的一阶偏导数 。
。
对称地,当固定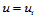 时,函数
时,函数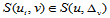 ,于是得到相应的
,于是得到相应的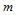 连续性方程
连续性方程
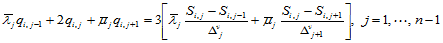 (10.2.9)
(10.2.9)
其中,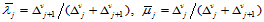 。
。
根据边界条件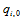 和
和 可求解上述方程组,即可求出
可求解上述方程组,即可求出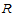 上所有节点
上所有节点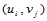 处的沿
处的沿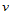 向的一阶偏导数
向的一阶偏导数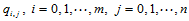 。
。
为了计算所有节点处的二阶混合偏导数,首先固定 ,则函数
,则函数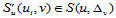 在各节点
在各节点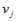 处的函数值
处的函数值 已从
已从 连续性方程(10.2.8)求出,因而得到关于
连续性方程(10.2.8)求出,因而得到关于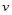 的三次样条函数
的三次样条函数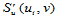 的
的 连续性方程
连续性方程
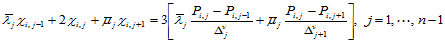 (10.2.10)
(10.2.10)
假如边界切向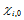 和
和 已知,那么就可由(10.2.10)解出
已知,那么就可由(10.2.10)解出 ,从而
,从而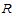 上所有节点
上所有节点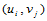 处的二阶混合偏导数
处的二阶混合偏导数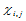 也就全部确定了。
也就全部确定了。
其实,边界切向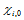 和
和 可按下述方法求得:沿
可按下述方法求得:沿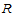 的两条边界
的两条边界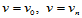 ,函数
,函数 ,
,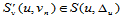 ,它们在各节点
,它们在各节点 处的函数值
处的函数值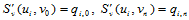 已从
已从 连续性方程(10.2.9)求出。于是,得到关于
连续性方程(10.2.9)求出。于是,得到关于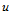 的三次样条函数
的三次样条函数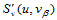 的
的 连续性方程
连续性方程
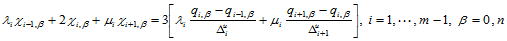 (10.2.11)
(10.2.11)
利用边界条件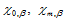 求解方程(10.2.11),即可求出
求解方程(10.2.11),即可求出 和
和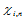 。
。
至此,矩阵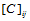 中所有元素均已求得,因此
中所有元素均已求得,因此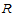 上的双三次样条函数
上的双三次样条函数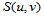 也被惟一确定了,它在各子矩形
也被惟一确定了,它在各子矩形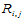 上的表示式就是式(10.2.7)。
上的表示式就是式(10.2.7)。
综上所述,在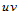 平面上给定了矩形区域
平面上给定了矩形区域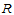 及矩形网格分割
及矩形网格分割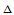 后,双三次插值样条函数
后,双三次插值样条函数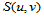 的计算步骤如下:
的计算步骤如下:
① 给定插值条件、边界条件;
②
依次求解四类三对角方程组(10.2.8)─(10.2.11),求出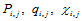 ,从而获得角点信息矩阵
,从而获得角点信息矩阵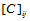 。这四类三对角方程组共有
。这四类三对角方程组共有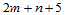 个,但它们的系数矩阵却只有两种形态,分别以数组
个,但它们的系数矩阵却只有两种形态,分别以数组 及
及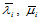 为特征。
为特征。
③
为了求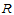 中任一点
中任一点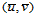 所对应的函数值
所对应的函数值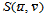 ,只要找出整数指标
,只要找出整数指标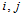 使得
使得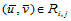 ,然后代入表达式计算即可。
,然后代入表达式计算即可。
定义在矩形域上带有矩形网格分割的双三次样条函数,我们解决的漂亮而又彻底,其关键之处在于:这里的二维分割是两个一维分割的直积,而且双三次样条函数又是两个一元三次样条函数的直积。这样,我们实际上把二元问题转化成两个方向上的一元问题了。
对于定义在一般平面区域上带有任意分割的二元样条函数这类问题的研究要困难的多,迄今所获得的理论成果和具体算法都是初步的,一般解仍然是一个发展中的课题。
当我们把双三次样条函数用于几何外形设计时,正如三次样条函数一样,只适用于小挠度场合,否则,光顺性同样可能被破坏。为了用于大挠度和多值场合,需要对双萨那次样条函数作些改造,其中最成功的一种方法就是采用参数双三次样条函数。
10.3 参数双三次样条曲面
给定三维空间呈矩形拓扑结构的一组数据点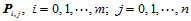 ,我们构造插值这些数据点的一张参数双三次样条曲面。根据10.2节对于双三次样条函数之讨论可知,必须给每一个数据点
,我们构造插值这些数据点的一张参数双三次样条曲面。根据10.2节对于双三次样条函数之讨论可知,必须给每一个数据点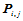 赋以相应的参数
赋以相应的参数 ,使其形成参数平面
,使其形成参数平面 上的一个矩形分割,这就是曲面数据点的参数化。
上的一个矩形分割,这就是曲面数据点的参数化。
10.3.1 曲面数据点的参数化
和曲线数据点的参数化一样,曲面数据点的参数化方法也有以下四种。
- 均匀参数化
使每一参数方向上的参数节点区间长度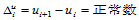 ,
, 。为处理方便起见,常取成整数序列:
。为处理方便起见,常取成整数序列:

结果形成参数平面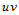 上的一个正方形网格分割。这种参数化法仅适合于每一参数方向上数据点均匀分布的情况。
上的一个正方形网格分割。这种参数化法仅适合于每一参数方向上数据点均匀分布的情况。
- 累加弦长参数化
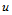 向的参数化为:
向的参数化为:
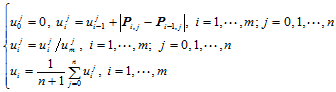 (10.3.1)
(10.3.1)
类似地,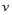 向的参数化为:
向的参数化为:
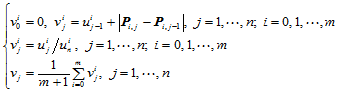 (10.3.2)
(10.3.2)
- 向心参数化
对于向心参数化来说, 向和
向和 向的参数化分别如下:
向的参数化分别如下:
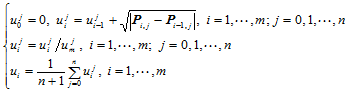 (10.3.3)
(10.3.3)
 (10.3.4)
(10.3.4)
- 修正弦长参数化
在修正弦长参数化下,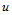 向的参数化为:
向的参数化为:
 (10.3.5)
(10.3.5)
其中:
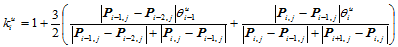
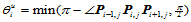
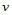 向的参数化类似:
向的参数化类似:
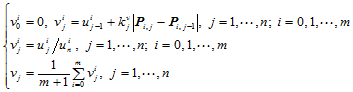 (10.3.6)
(10.3.6)
这里:

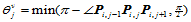
在后三种参数化中,我们之所以进行规范化、平均化,其主要原因是沿同一参数方向的网格线应具有公共的参数分割,而在该方向上的各排数据点分布状况一般不一样。由其分布状况决定的各参数分割也就不一样,那么公共的参数分割只能是它们的混合或折中。
当然,具体决定参数化时还应根据实际情况及要求,确定切合实际需要的参数化,不能生搬硬套上述方法。例如,当数据点沿纵向(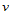 向)依次在各横截面内给出时,那么横截面方向(
向)依次在各横截面内给出时,那么横截面方向(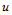 向)的参数分割可按上述的平均规范参数化给出,而纵向(
向)的参数分割可按上述的平均规范参数化给出,而纵向( 向)的参数分割则应视各横截面在空间的分布情况给出。
向)的参数分割则应视各横截面在空间的分布情况给出。
参数双三次样条曲面方程
一旦参数分割 和
和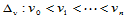 确定后,利用双三次样条函数的构造方法,我们立即可以给出分片定义在子矩形区域
确定后,利用双三次样条函数的构造方法,我们立即可以给出分片定义在子矩形区域 上的用角点信息矩阵表示的参数双三次样条曲面方程:
上的用角点信息矩阵表示的参数双三次样条曲面方程:
 (10.3.7)
(10.3.7)
其中:

这里,角点信息矩阵中的左下角、右上角以及右下角三个二阶子阵中的四个元素分别为该曲面片在四个角点处的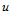 向切矢、
向切矢、 向切矢与二阶混合偏导矢,是未知待定的。
向切矢与二阶混合偏导矢,是未知待定的。
未知偏导矢的求解
与双三次样条函数的求解方法一样,为了确定每个网格点处的三个未知量,只需事先给定边界条件即可。具体确定各网格点处未知量的步骤如下:
1. 固定下标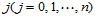 ,以数据点
,以数据点 ,及边界条件
,及边界条件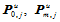 在参数分割
在参数分割 上构造参数三次样条曲线,可求出所有网格点处的
上构造参数三次样条曲线,可求出所有网格点处的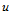 向切矢
向切矢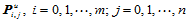 。
。
2. 固定下标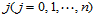 ,以
,以 ,为数据点,
,为数据点,
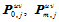 为边界条件在参数分割
为边界条件在参数分割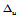 上构造参数三次样条曲线,解出的"未知切矢"即为
上构造参数三次样条曲线,解出的"未知切矢"即为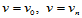 两边上的各网格点处的二阶混合偏导矢
两边上的各网格点处的二阶混合偏导矢 。
。
3. 固定下标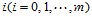 ,以数据点
,以数据点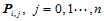 ,及边界条件
,及边界条件 在参数分割
在参数分割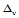 上构造参数三次样条曲线,可求出所有网格点处的
上构造参数三次样条曲线,可求出所有网格点处的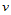 向切矢
向切矢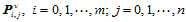 。
。
4. 固定下标 ,以
,以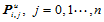 ,为数据点,
,为数据点,
 为边界条件在参数分割
为边界条件在参数分割 上构造参数三次样条曲线,求出的"未知切矢"即为所有网格点处的二阶混合偏导矢
上构造参数三次样条曲线,求出的"未知切矢"即为所有网格点处的二阶混合偏导矢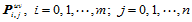 。
。
当然,上述四步也可以换成不同的顺序,也可采用其他的边界条件。
10.3.4 计算插值曲面
求解出所有的角点信息之后,就可惟一确定一参数双三次样条曲面。那么,对于定义域 内任一点
内任一点 ,求曲面上对应的点
,求曲面上对应的点 及其他几何信息时,首先确定
及其他几何信息时,首先确定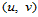 所在的子区域
所在的子区域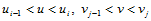 ,然后依据曲面片的指标
,然后依据曲面片的指标 ,选取相应的曲面片表达式计算即可。
,选取相应的曲面片表达式计算即可。
10.4 Ferguson样条曲面
在参数双三次样条曲面中,如果我们采用均匀参数化,且取每一个网格点处的二阶混合偏导矢为零矢量,那么所对应的参数双三次样条曲面称为Ferguson样条曲面,其分片表示式如下:
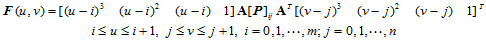 (10.4.1)
(10.4.1)
其中:
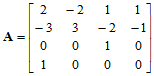 (10.4.2)
(10.4.2)
 (10.4.3)
(10.4.3)
在这种情况下,未知量 所满足的方程退化为:
所满足的方程退化为:
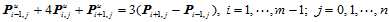 (10.4.5)
(10.4.5)
和
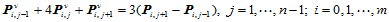 (10.4.6)
(10.4.6)
只要给定边界条件 和
和 ,即可求解出每一网格点处的两个切矢。
,即可求解出每一网格点处的两个切矢。
Ferguson样条曲面的网格线都是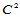 连续的,然而整个样条曲面却仅为
连续的,然而整个样条曲面却仅为 连续的,而且所有角点处的二阶混合偏导矢取成零矢量,可能会导致所生成的曲面片在角点附近局部变得平坦,其内部形状也不一定合适。
连续的,而且所有角点处的二阶混合偏导矢取成零矢量,可能会导致所生成的曲面片在角点附近局部变得平坦,其内部形状也不一定合适。
10.5 Coons双三次样条曲面
如果我们仍采用均匀参数化,且允许网格点处的二阶混合偏导矢非零,那么这类参数双三次样条曲面就称为Coons双三次样条曲面。Coons双三次样条曲面的分片表示式与Ferguson曲面片的表示式相同,惟一的区别是角点信息矩阵中右下角的二阶子阵的四个元素非零。所有的未知偏导矢满足以下方程:
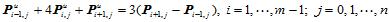 (10.5.1)
(10.5.1)
 (10.5.2)
(10.5.2)
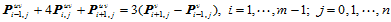 (10.5.3)
(10.5.3)
或
 (10.5.4)
(10.5.4)
Coons双三次样条曲面是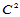 连续的,它只是Coons曲面的特例,有关一般Coons曲面的讨论,我们将在第十五章中给出。
连续的,它只是Coons曲面的特例,有关一般Coons曲面的讨论,我们将在第十五章中给出。




