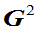
样条的基函数
前面我们讨论了两类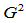 三次样条曲线:Gamma样条与组合Bézier样条。显然,从设计的角度来看,组合Bézier样条优于Gamma样条。因为Bézier样条只需给定控制顶点,而Gamma样条的构造还需要节点序列和形状参数
三次样条曲线:Gamma样条与组合Bézier样条。显然,从设计的角度来看,组合Bézier样条优于Gamma样条。因为Bézier样条只需给定控制顶点,而Gamma样条的构造还需要节点序列和形状参数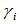 。然而,Gamma样条的优势在于对
。然而,Gamma样条的优势在于对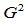 样条分析性质的讨论。下面,我们就
样条分析性质的讨论。下面,我们就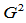 样条的分析性质进行讨论。
样条的分析性质进行讨论。
设Gamma样条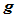 和
和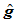 由相同的节点序列和相同的形状参数
由相同的节点序列和相同的形状参数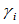 所定义,相应的控制顶点分别为
所定义,相应的控制顶点分别为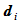 和
和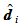 ,那么曲线:
,那么曲线:
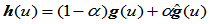
也是一Gamma样条,其节点序列和形状参数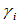 不变,但控制顶点则为:
不变,但控制顶点则为:
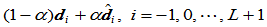
这一线性性质的结果是,由相同节点序列和形状参数确定的Gamma样条构成一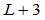 维线性空间。设该空间的基函数为
维线性空间。设该空间的基函数为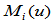 ,则任何一元素(Gamma样条)可表示为:
,则任何一元素(Gamma样条)可表示为:
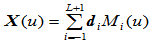
这里,基函数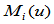 由参数
由参数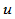 、节点序列
、节点序列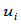 和形状参数
和形状参数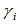 所确定,具有以下性质:
所确定,具有以下性质:
① 归一性。Gamma样条的构造是仿射不变的,着意味着:
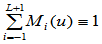
②
正性。对满足条件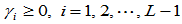 ,形状参数,有:
,形状参数,有:
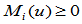
③
局部支撑性。顶点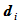 的改变知影响到四段曲线:
的改变知影响到四段曲线: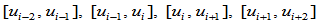 ,因此相应的基函数
,因此相应的基函数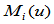 满足条件:
满足条件:
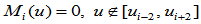
这一性质成立的原因是,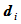 的改变不影响曲线的Bézier点
的改变不影响曲线的Bézier点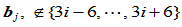 。此外,
。此外,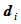 的改变也不影响内Bézier点
的改变也不影响内Bézier点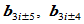 ,因此还有下述性质。
,因此还有下述性质。
④ 端点可导性。
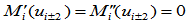
基于以上性质,我们可构造出基函数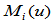 。
。
给定控制顶点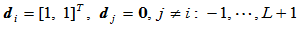 ,构造Gamma样条曲线
,构造Gamma样条曲线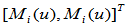 。利用坐标图
。利用坐标图 即可求出
即可求出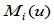 的Bézier纵标:
的Bézier纵标:
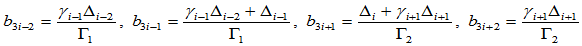 (9.7.1)
(9.7.1)
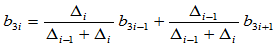 (9.7.2)
(9.7.2)
其中,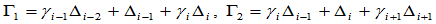 ,而
,而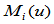 的所有其余Bézier纵标为零。
的所有其余Bézier纵标为零。
由构造过程可知, 是
是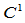 连续的,但不是
连续的,但不是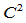 连续,甚至也不是
连续,甚至也不是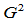 连续。这似乎有点不可思议,曲率不连续的函数的组合竟然生成曲率连续的曲线,下面我们仔细探究这一点。
连续。这似乎有点不可思议,曲率不连续的函数的组合竟然生成曲率连续的曲线,下面我们仔细探究这一点。
一条Gamma样条必然满足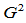 连续性条件,那么曲线的每一个坐标分量亦自然满足这一条件。由
连续性条件,那么曲线的每一个坐标分量亦自然满足这一条件。由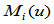 的构造可知:
的构造可知:
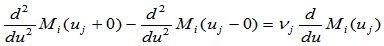
所谓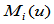 的
的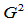 连续性,是指它的图形
连续性,是指它的图形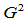 连续,它是二维曲线
连续,它是二维曲线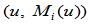 。由于一般情况下参数
。由于一般情况下参数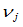 非零,因此坐标分量
非零,因此坐标分量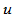 并不满足
并不满足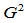 连续性条件,所以
连续性条件,所以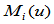 不是
不是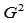 连续的。
连续的。
由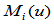 所满足的
所满足的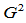 条件,能够导出连续性
条件,能够导出连续性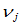 和
和 之间的关系:
之间的关系:
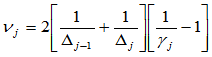 (9.7.3)
(9.7.3)
这就在Nu样条和Gamma样条之间建立了联系。
Beta样条
Gamma样条的构造与Nu样条一样,是从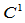 条件出发的。如果我们直接从
条件出发的。如果我们直接从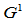 条件出发构造
条件出发构造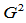 三次样条曲线,便得到Beta样条。由几何连续的定义9.3,两段
三次样条曲线,便得到Beta样条。由几何连续的定义9.3,两段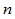 次Bézier曲线
次Bézier曲线
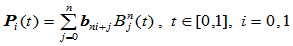
在公共连接点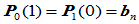 处
处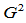 连续的条件是:
连续的条件是:

将其用Bézier点表示,则为:
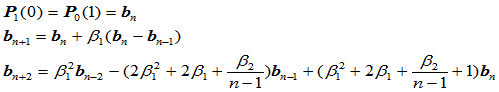 (9.8.1)
(9.8.1)
本是几何问题,人们更乐于采用几何方法。因此,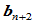 的确定并不是象式(9.8.1)那样用代数方程组,而是用图9.5所示的几何方法。
的确定并不是象式(9.8.1)那样用代数方程组,而是用图9.5所示的几何方法。
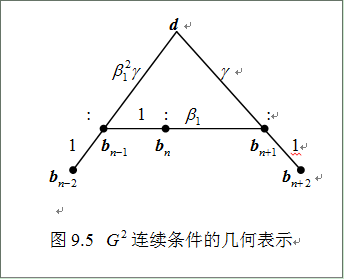
那么以控制顶点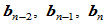 和形状参数
和形状参数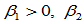 作为输入,生成的控制顶点
作为输入,生成的控制顶点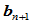 ,
,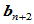 为输出,使组合Bézier曲线在
为输出,使组合Bézier曲线在 处满足
处满足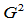 连续条件的构造过程如下:
连续条件的构造过程如下:
Step1. 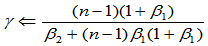 ;
;
Step2. 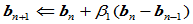 ;
;
Step3. 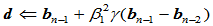 ;
;
Step4. 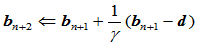 。
。
基于以上讨论,我们可以构造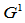 、
、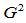 连续的组合二次、三次Bézier曲线,它们被称为Beta样条曲线。
连续的组合二次、三次Bézier曲线,它们被称为Beta样条曲线。
9.8.1 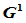 二次Beta样条曲线
二次Beta样条曲线
给定控制顶点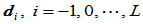 ,和形状参数
,和形状参数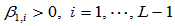 ,一条
,一条 Beta样条曲线的第
Beta样条曲线的第 段
段
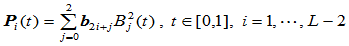
的Bézier点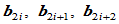 由控制顶点
由控制顶点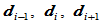 和形状参数
和形状参数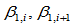 按如下步骤确定:
按如下步骤确定:
①
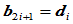 ;
;
②
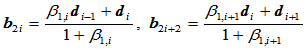 。
。
其中,第一段和第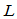 段的控制顶点为:
段的控制顶点为:

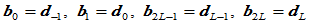
特别,当所有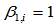 时,所有连接点
时,所有连接点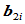 均为控制多边形相应边的中点,
均为控制多边形相应边的中点,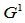 二次Beta样条曲线就成为
二次Beta样条曲线就成为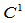 二次均匀B样条曲线。
二次均匀B样条曲线。
9.8.2 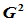 三次Beta样条曲线
三次Beta样条曲线
给定控制顶点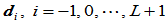 ,和两组形状参数
,和两组形状参数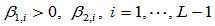 ,由其定义由
,由其定义由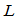 段三次Bézier曲线组成的
段三次Bézier曲线组成的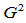 Beta样条曲线,其第
Beta样条曲线,其第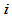 段
段
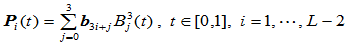
的Bézier点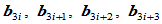 由控制顶点
由控制顶点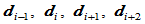 和形状参数
和形状参数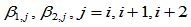 所确定,其计算步骤按如下:
所确定,其计算步骤按如下:
① 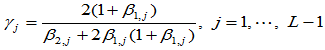 ;
;
②
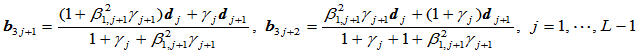 ;
;
③ 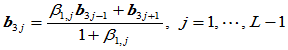 ;
;
④ 边界条件如下:
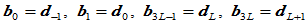

特别,当所有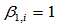 、
、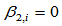 时,
时, 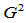 三次Beta样条曲线便退化为
三次Beta样条曲线便退化为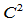 三次均匀B样条曲线。
三次均匀B样条曲线。
对于给定的控制顶点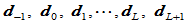 ,节点序列
,节点序列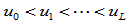 及形状参数
及形状参数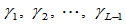 ,如果令:
,如果令:
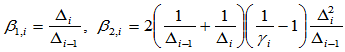
那么,我们便得到了Gamma样条。因此,Beta样条是Gamma样条的推广。
9.9 有理参数曲线的连续性
对于有理Bézier曲线那样的有理参数曲线,单一的有理曲线段往往没有足够的自由度表示一给定的曲线,因而不能满足曲线设计的要求,替代单一有理曲线段的是分段有理曲线。为了生成一条具有满意光滑度的曲线,构成组合曲线的各曲线段必须按照某种连续性连接起来。
对于有理参数曲线,如果用齐次坐标表示的非有理曲线满足有关连续性约束,那么它的投影即有理曲线也将具有相应的连续性。但反过来则不成立。如果有理曲线具有这些连续性,则相应它的齐次曲线并非一定要满足这些约束。也就是说,要求齐次曲线象它的投影曲线那样光滑是限制过头了。我们希望对和有理曲线对应的齐次曲线的连续性有尽可能少的限制,以使有理曲线的连续拼接易于实现。
设有理曲线 由控制顶点
由控制顶点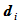 和权因子
和权因子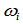 定义:
定义:
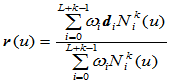
由带权控制顶点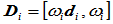 在高一维空间定义的非有理曲线即齐次曲线记为
在高一维空间定义的非有理曲线即齐次曲线记为 ,则:
,则:
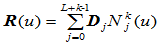
若令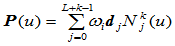 ,
,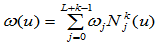 ,则有:
,则有:
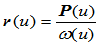 ,
,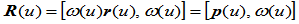
9.9.1 有理参数连续性条件
设定义在分割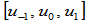 上的两有理曲线段
上的两有理曲线段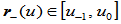 与
与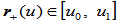 组合成一有理曲线
组合成一有理曲线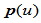 ,它们在
,它们在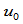 处具有公共的左右连接点
处具有公共的左右连接点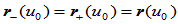 ,然而相应的两齐次点
,然而相应的两齐次点 与
与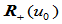 可以不是同一点,即
可以不是同一点,即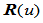 在
在 处可以位置不连续,只需满足条件:
处可以位置不连续,只需满足条件:
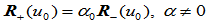 (9.9.1)
(9.9.1)
即当两齐次点位置矢量互为标量倍数时,则它们具有相同的投影点。
下面我们考察切矢连续性。对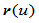 关于
关于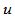 求一阶导矢,令其在
求一阶导矢,令其在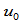 处的左右切矢相等,即
处的左右切矢相等,即 ,则有:
,则有:
 (9.9.2)
(9.9.2)
这表明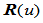 在
在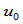 处的左右切矢的差矢量平行于齐次点位置矢量
处的左右切矢的差矢量平行于齐次点位置矢量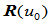 (当
(当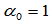 时)。
时)。
按照上述方法继续逐一考察,则可得到高阶参数连续性的约束条件:
齐次曲线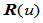 的投影即有理曲线
的投影即有理曲线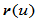 在参数
在参数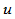 处
处 连续,当且仅当存在常数
连续,当且仅当存在常数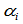 ,
,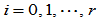 ,使得下列约束成立:
,使得下列约束成立:
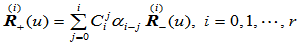 (9.9.3)
(9.9.3)
写成矩阵形式,有
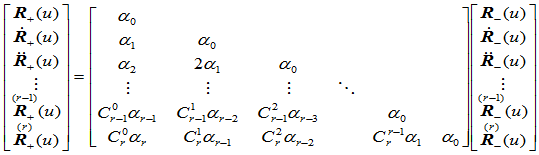 (9.9.4)
(9.9.4)
该公式的推导借助于喷射空间(Jet Space)的概念。
9.9.2 有理几何连续性条件
齐次曲线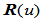 的投影即有理曲线
的投影即有理曲线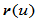 是
是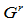 连续的,当且仅当存在两组实数
连续的,当且仅当存在两组实数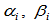 ,
,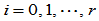 ,使得下述约束条件成立:
,使得下述约束条件成立:
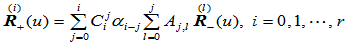 (9.9.5)
(9.9.5)
这里, 是Beta约束中的系数。
是Beta约束中的系数。
上述条件若写成矩阵形式,则有:
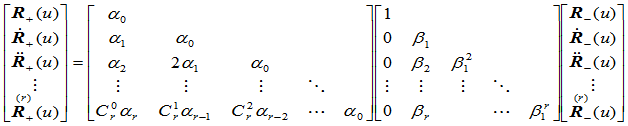 (9.9.6)
(9.9.6)
例如当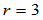 时,有:
时,有:
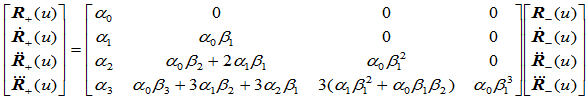
如果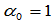 ,其余的
,其余的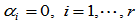 ,则有理几何约束简化成Beta约束;如果
,则有理几何约束简化成Beta约束;如果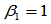 ,其余的
,其余的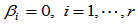 ,则有理几何约束退化为有理参数约束了。
,则有理几何约束退化为有理参数约束了。
与Beta约束不同的是,在有理几何约束中包含两组参数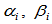 。例如,在
。例如,在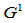 的Beta约束中仅有一个自由度
的Beta约束中仅有一个自由度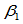 ,而在
,而在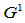 有理几何约束中,则有三个自由度
有理几何约束中,则有三个自由度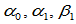 。其原因在于,对于正则的投影曲线,有
。其原因在于,对于正则的投影曲线,有
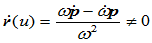
即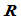 和
和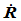 是线性独立的。因此,每个有理几何连续性总能提供两个独立的自由度。
是线性独立的。因此,每个有理几何连续性总能提供两个独立的自由度。
9.9.3 Frenet标架连续性
Frenet标架连续性是几何连续性的两种形式之一,它就是Boehm所指的几何不变量的连续性。前面介绍的有理几何连续条件实质上可归结为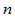 阶切触连续性。
阶切触连续性。
Frenet标架连续性是建立在高维空间的广义曲率基础上的。设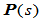 是
是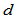 维空间的一条以弧长
维空间的一条以弧长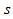 为参数的曲线,则它的Frenet标架及高阶曲率定义如下:
为参数的曲线,则它的Frenet标架及高阶曲率定义如下:
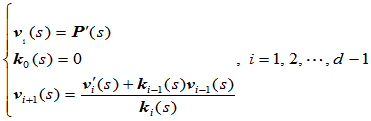 (9.9.7)
(9.9.7)
此处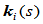 的选取应使
的选取应使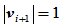 。显然,
。显然, 是
是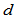 维空间的一组正交基,称之为曲线
维空间的一组正交基,称之为曲线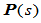 的Frenet标架。
的Frenet标架。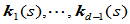 叫做曲线
叫做曲线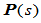 的一阶曲率、二阶曲率、…、
的一阶曲率、二阶曲率、…、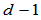 阶曲率,各阶曲率都是曲线的几何不变量。
阶曲率,各阶曲率都是曲线的几何不变量。
当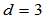 时,那么
时,那么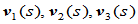 分别就是曲线的切矢、主法矢和副法矢,
分别就是曲线的切矢、主法矢和副法矢,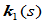 是曲线的曲率,
是曲线的曲率,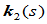 是曲线的二阶曲率即挠率。
是曲线的二阶曲率即挠率。
 维空间的曲线有
维空间的曲线有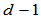 个几何不变量。一般地,除一个刚体运动外,作为曲线弧长函数的这
个几何不变量。一般地,除一个刚体运动外,作为曲线弧长函数的这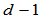 个几何不变量定义了惟一一条
个几何不变量定义了惟一一条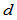 维空间曲线。从这个意义上讲,
维空间曲线。从这个意义上讲,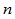 阶几何连续也可被定义为曲线直到
阶几何连续也可被定义为曲线直到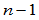 阶曲率的几何不变量的连续性。由此,便有以下的Frenet标架连续性的定义。
阶曲率的几何不变量的连续性。由此,便有以下的Frenet标架连续性的定义。
定义9.5 一条曲线是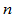 阶Frenet标架连续性的(记为
阶Frenet标架连续性的(记为 ),当且仅当它的弧长参数化的Frenet标架矢量和广义曲率是连续的。
),当且仅当它的弧长参数化的Frenet标架矢量和广义曲率是连续的。
Frenet标架连续性在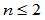 时与前述的几何连续性一致。对于
时与前述的几何连续性一致。对于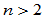 ,
,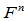 是
是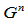 的推广,但不同于
的推广,但不同于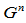 。当
。当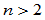 时,存在
时,存在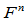 连续的曲线,却不是
连续的曲线,却不是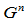 连续的。应当注意,在
连续的。应当注意,在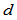 维空间所有
维空间所有 连续的曲线通常也将是
连续的曲线通常也将是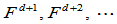 连续的。例如,所有
连续的。例如,所有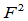 连续的平面曲线是
连续的平面曲线是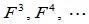 连续的,所有
连续的,所有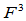 连续的空间曲线是
连续的空间曲线是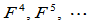 连续的。因此,
连续的。因此,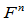 连续性仅仅在曲线的维数
连续性仅仅在曲线的维数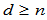 时才有意义。在
时才有意义。在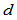 维空间的Frenet标架连续性仅仅能区分
维空间的Frenet标架连续性仅仅能区分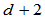 类曲线:位置不连续曲线、位置连续曲线、
类曲线:位置不连续曲线、位置连续曲线、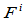 连续但非
连续但非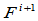 连续曲线,
连续曲线,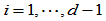 ,和
,和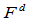 连续曲线,而
连续曲线,而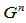 连续性却可以区分无穷多类曲线。
连续性却可以区分无穷多类曲线。
一条曲线 是
是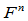 连续的,当且仅当存在一个Frenet标架矩阵
连续的,当且仅当存在一个Frenet标架矩阵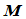 使得:
使得:
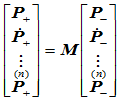 (9.9.8)
(9.9.8)
矩阵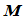 称之为关联矩阵,它是一下三角
称之为关联矩阵,它是一下三角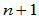 阶方阵,其主对角线元素为
阶方阵,其主对角线元素为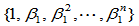 ,第一列元素除首行元素外均为零,而其余的
,第一列元素除首行元素外均为零,而其余的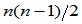 个元素任意,即:
个元素任意,即:
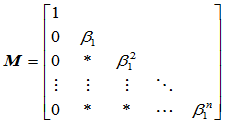 (9.9.9)
(9.9.9)
9.9.4 有理Frenet标架连续性约束
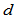 维空间的有理曲线
维空间的有理曲线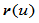 是
是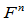 连续的,当且仅当齐次曲线
连续的,当且仅当齐次曲线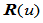 的单边导矢存在且满足以下约束:
的单边导矢存在且满足以下约束:
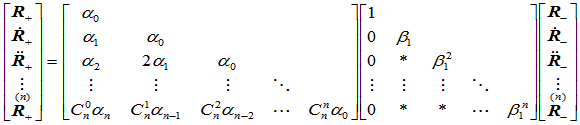 (9.9.10)
(9.9.10)
9.10 几何连续的有理参数样条曲线
参数连续性与参数的选取有关。在二阶与三阶时,Frenet标架连续性与几何连续性是相一致的。针对工业产品形状的数学描述来说,几何连续性是适合需要的。本节我们直接基于对有理曲线的几何连续性的分析来构造有理样条曲线。
9.10.1 曲率连续的有理二次样条曲线
传统上,用二次曲线弧构造 的分段二次曲线时,为了达成曲率连续,必须采用分段三次。应用几何连续性,便可以用有理二次Bézier曲线设计曲率连续的平面曲线。为了避免引起混淆,对于平面曲线,采用相对曲率,它与
的分段二次曲线时,为了达成曲率连续,必须采用分段三次。应用几何连续性,便可以用有理二次Bézier曲线设计曲率连续的平面曲线。为了避免引起混淆,对于平面曲线,采用相对曲率,它与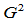 连续性是等价的。
连续性是等价的。
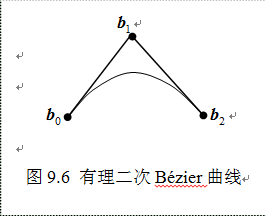
对于给定的有理二次曲线段:
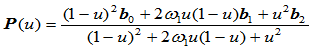
其首末端点相对曲率为:
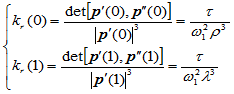 (7.9.1)
(7.9.1)
其中: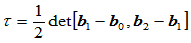 为
为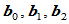 构成的三角形的有向面积,
构成的三角形的有向面积,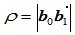 ,
,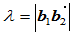 。
。
假设有一平面曲线,它是由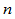 段有理二次曲线组合而成,其中第
段有理二次曲线组合而成,其中第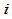 段由控制顶点
段由控制顶点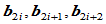 和权因子
和权因子 定义。那么,
定义。那么,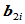 则为第
则为第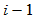 段与第
段与第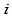 段的公共连接点。如果
段的公共连接点。如果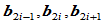 三个顶点共线,且
三个顶点共线,且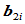 位于
位于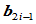 与
与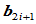 之间,则相邻两段曲线在公共连接点处
之间,则相邻两段曲线在公共连接点处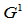 连续的。
连续的。
为了使第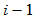 段与第
段与第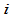 段在
段在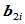 处达到曲率连续,它们必须在
处达到曲率连续,它们必须在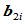 处有相同的相对曲率。根据前面的约定,第
处有相同的相对曲率。根据前面的约定,第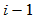 段与第
段与第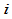 段在
段在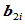 处的相对曲率分别为:
处的相对曲率分别为:
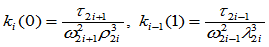 ,
,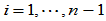 (9.10.1)
(9.10.1)
其中
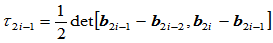
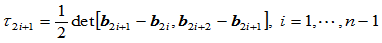
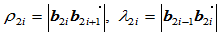
因此,曲率连续即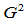 连续的条件是:
连续的条件是:
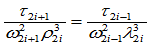 ,
,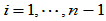 (9.10.2)
(9.10.2)
这表明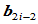 ,
,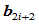 两点位于
两点位于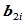 处切线的同一侧,且权因子
处切线的同一侧,且权因子 与
与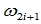 满足条件:
满足条件:
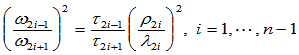 (9.10.3)
(9.10.3)
如果一分段有理二次曲线在所有连接处都有连续曲率,那么我们按一公共比例因子改变所有内权因子 ,则由上述条件可知曲线在连接处仍然保持曲率连续。然而,在连接点处的相对曲率已经发生变化,曲线的形状也已改变。如果增大这一公共比例因子,曲线段将趋近它们的控制多边形。反之,将趋近它们的弦线。因此,这一公共因子可被看作形状参数。
,则由上述条件可知曲线在连接处仍然保持曲率连续。然而,在连接点处的相对曲率已经发生变化,曲线的形状也已改变。如果增大这一公共比例因子,曲线段将趋近它们的控制多边形。反之,将趋近它们的弦线。因此,这一公共因子可被看作形状参数。
下面我们着重讨论曲率连续的平面有理二次样条曲线的构造。
- 设
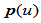 是
是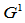 连续的分段有理二次曲线,且有内权因子
连续的分段有理二次曲线,且有内权因子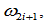
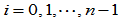 。在保持控制多边形不变的情况下,能否找到新的内权因子
。在保持控制多边形不变的情况下,能否找到新的内权因子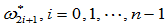 ,使
,使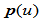 为曲率连续的分段有理二次曲线
为曲率连续的分段有理二次曲线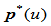 。
。
根据曲率连续性条件,可知:
 (9.10.4)
(9.10.4)
因此,只要选定权因子
 之后,按照上式即可计算出所有的新权因子
之后,按照上式即可计算出所有的新权因子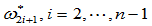 。由这一组新权因子和原控制多边形便可确定一条曲率连续的分段有理二次曲线
。由这一组新权因子和原控制多边形便可确定一条曲率连续的分段有理二次曲线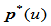
显然上式只有当右边非负才有解。右边为正的条件是
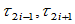 同号。几何上意味着
同号。几何上意味着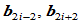 位于线段
位于线段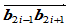 之同侧,因而
之同侧,因而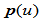 的控制多边形应是局部凸多边形。
的控制多边形应是局部凸多边形。
- 给定一局部凸的控制多边形
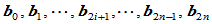 ,求以
,求以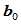 为起点,以
为起点,以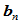 为终点的一条曲率连续的分段有理二次样条曲线
为终点的一条曲率连续的分段有理二次样条曲线 。
。
对此问题求解的关键是找连接点
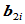 和内权因子
和内权因子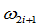 ,为此在边
,为此在边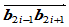 上任取一点作为
上任取一点作为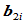 ,就可按照(1)中的方法求出
,就可按照(1)中的方法求出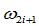 。
。
(3)给定一封闭的凸多边形
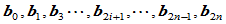 ,其中
,其中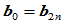 ,且位于边
,且位于边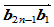 上,构造一曲率连续的分段有理二次样条曲线
上,构造一曲率连续的分段有理二次样条曲线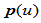 ,显然
,显然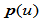 是一条封闭曲线。
是一条封闭曲线。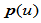 的构造与(2)基本相同。在边
的构造与(2)基本相同。在边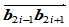 上选取一连接点
上选取一连接点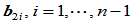 ,根据连续性条件可知:
,根据连续性条件可知:
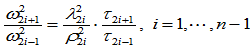 (9.10.5)
(9.10.5)
上式简记如下:
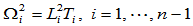
由于
 也是一个连接点,曲线
也是一个连接点,曲线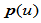 在该点也要求曲率连续,那么有
在该点也要求曲率连续,那么有
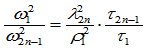 (9.10.6)
(9.10.6)
简记为
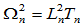 。
。
将上式
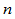 个方程左右相乘,则有:
个方程左右相乘,则有:
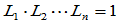 (9.10.7)
(9.10.7)
这一条件称为相容性条件。因此,连接点
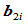 在边
在边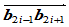 上的位置便不能任意选取了,必须使上述相容性条件得到满足。达到这一要求的方法是令:
上的位置便不能任意选取了,必须使上述相容性条件得到满足。达到这一要求的方法是令:
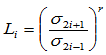
其中
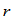 为实数,
为实数,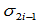 为三角形
为三角形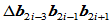 的有向面积。
的有向面积。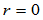 时,连接点
时,连接点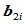 即为边
即为边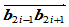 的中点。
的中点。
由以上讨论可见,我们用最低次的曲线段实现了曲率连续的分段平面曲线的构造,并且还提供了可作为形状参数实现对曲线形状控制的一个公共因子。当然,这里可调的形状参数仅仅是一个公共因子,这意味着只能对曲线实现整体形状控制。
9.10.2 曲率连续的有理三次样条曲线
(1)几何连续性条件
设由相邻的两段有理
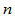 次Bézier曲线构成的组合曲线
次Bézier曲线构成的组合曲线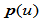 定义在参数区间
定义在参数区间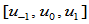 上,左右两段分别由控制顶点、权因子
上,左右两段分别由控制顶点、权因子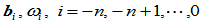 和
和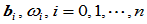 定义,连接点
定义,连接点 对应参数
对应参数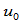 。
。
记
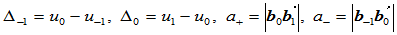 ,
,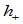 为
为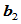 到
到 的距离,
的距离,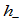 为
为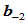 到
到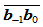 的距离,
的距离,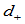 为
为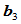 到
到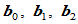 所张成的平面的距离,
所张成的平面的距离,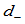 为
为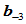 到
到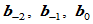 所张成的平面的距离(图9.7),那么
所张成的平面的距离(图9.7),那么
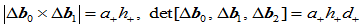
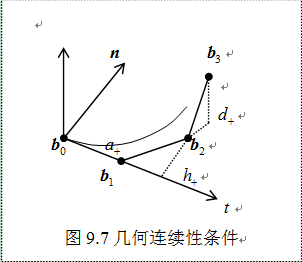
曲线
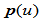 在连接点
在连接点 处左右两侧的曲率与挠率分别为:
处左右两侧的曲率与挠率分别为:

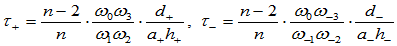
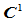 连续性条件:
在连接点
连续性条件:
在连接点 处
处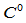 连续的分段有理
连续的分段有理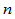 次Bézier曲线
次Bézier曲线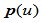 ,如果
,如果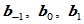 三点共线,
三点共线,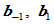 位于
位于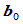 的两侧,且
的两侧,且
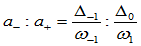 (9.10.8)
(9.10.8)
则
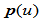 在
在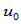 处
处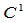 连续。
连续。
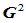 连续性条件:在连接点
连续性条件:在连接点 处
处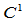 连续的分段有理
连续的分段有理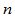 次Bézier曲线
次Bézier曲线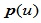 ,如果五点
,如果五点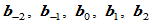 共面,
共面,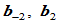 位于
位于 处切线的同侧,且
处切线的同侧,且
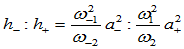 (9.10.9)
(9.10.9)
则
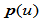 在
在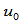 处
处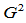 连续。应用
连续。应用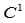 连续性条件,上式可化简为:
连续性条件,上式可化简为:
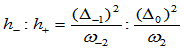
挠率连续性条件:在连接点
 处
处 连续的分段有理
连续的分段有理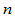 次Bézier曲线
次Bézier曲线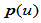 ,如果
,如果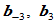 位于
位于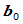 处密切平面线的两侧,且
处密切平面线的两侧,且
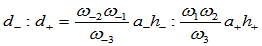 (9.10.10)
(9.10.10)
则
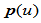 在
在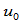 处挠率连续。应用
处挠率连续。应用 连续性条件,上式可化简为:
连续性条件,上式可化简为:
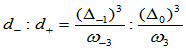
(2)曲率连续的有理三次样条曲线的构造
现考虑两相邻的有理三次Bézier曲线段,其定义区间分别为
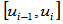 和
和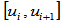 。在连接点
。在连接点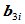 处,Bézier点
处,Bézier点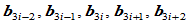 张成
张成 处的密切平面
处的密切平面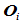 ,因此边
,因此边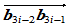 与
与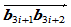 或者平行或者相交于一点
或者平行或者相交于一点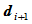 。假设
。假设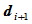 存在,设
存在,设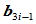 和
和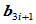 分别以比例
分别以比例 和
和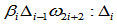 分连线
分连线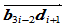 与
与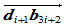 ,那么由上述的
,那么由上述的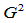 连续条件可知,两段曲线在
连续条件可知,两段曲线在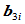 处
处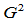 连续等价于
连续等价于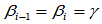 。又由
。又由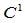 连续条件,
连续条件,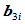 以比例
以比例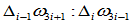 分连线
分连线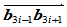 。因此,我们可以用辅助顶点
。因此,我们可以用辅助顶点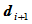 来构造曲率连续的分段有理三次Bézier曲线。
来构造曲率连续的分段有理三次Bézier曲线。
给定三维空间的控制多边形顶点
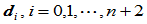 及整体参数
及整体参数 的相应节点
的相应节点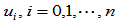 ,权因子
,权因子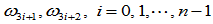 及参数
及参数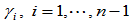 ,可构造一条曲率连续的分段有理三次Bézier曲线,构造过程如下:
,可构造一条曲率连续的分段有理三次Bézier曲线,构造过程如下:
- 给定一局部凸的控制多边形
- 按比例
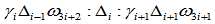 分割多边形
分割多边形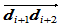 确定内Bézier点
确定内Bézier点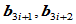 ,
,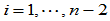 ;
;
- 按比例
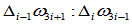 分割
分割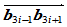 之连线确定
之连线确定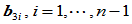 ;
;
- 首末两段Bézier点确定如下:
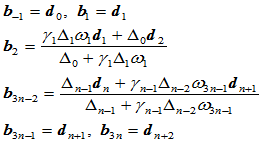
若所有权因子
 时,所构造的曲线将是非有理三次曲率连续的样条曲线,在内节点
时,所构造的曲线将是非有理三次曲率连续的样条曲线,在内节点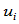 处带有张力参数
处带有张力参数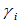 ,这就是Gamma样条。若又所有的张力参数
,这就是Gamma样条。若又所有的张力参数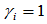 ,则所构造的曲线便为标准的
,则所构造的曲线便为标准的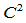 三次样条曲线。
三次样条曲线。



