第五章 大数定律和中心极限定理
§1 大数定律
设X1,X2,...Xn,...是一随机变量列,a1,a2,...an,...是一常数列,令Yn=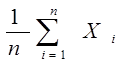 n=1,2,...,,所谓大数定律就是研究(Yn-an)收敛到0的定理。按收敛意义的不同,有弱大数定律和强大数定律。我们主要介绍弱大数定律,弱大数定律也称大数定律。
n=1,2,...,,所谓大数定律就是研究(Yn-an)收敛到0的定理。按收敛意义的不同,有弱大数定律和强大数定律。我们主要介绍弱大数定律,弱大数定律也称大数定律。
契比雪夫不等式
设R.V.X,其 都存在,则对任意
都存在,则对任意 均有
均有
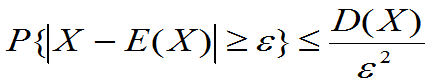
或
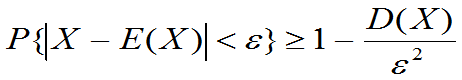
一、大数定律
定理5.1:(契比雪夫大数定律)
若X1,X2,...Xn,...相互独立,它们的数学期望和方差都存在,且方差一致有界,即E(X i)=mi, D(Xi)=si2£C(常数) i=1,2,...
则对任意的e>0,均有
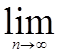 P{êYn-E(Yn)ï<e}=1 (5.1)
P{êYn-E(Yn)ï<e}=1 (5.1)
其中Yn=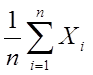
定理5.2(伯努利大数定律)
设伯努利试验中,事件A发生的概率为p(0<p<1),m为n重伯努利试验中事件A发生的次数,则对任意的e>0,均有
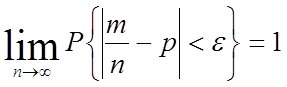 (5.2)
(5.2)
定理5.3 (辛钦大数定律)
若X1,X2,...,Xn,...相互独立同分布,其数学期望存在,即E(Xi)=m,i=1,2,...,则对任意的e>0,均有
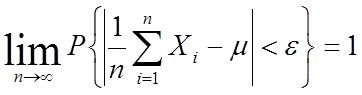 (5.3)
(5.3)
例:设X1,X2,...,Xn,...独立同分布,且X i的k阶矩m k=E(X ik)存在(k为正整数),则对任意的e>0,均有
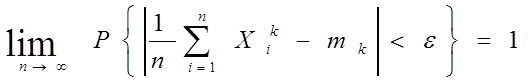
二、中心极限定理
定理5.4 (林德贝格-莱维定理)
若X1,X2,...,Xn,...相互独立同分布,其数学期望和方差均存在且方差大于零,即E(Xi)=m, D(Xi)=s2>0, i=1,2,...则 的标准化随机变量
的标准化随机变量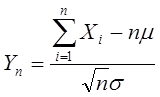 的分布函数
的分布函数 对于任意的x满足
对于任意的x满足
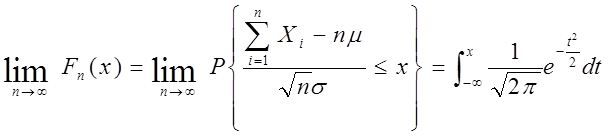
即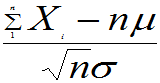 的分布函数
的分布函数
 .
.
当 很大时近似公式
很大时近似公式
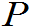
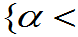
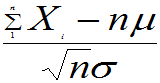
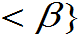
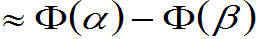 .
.
例:为了把问题简化,假定在计算机上进行加法计算时,对每个数都取最接近它的整数(即取整)再相加。设n个数取整之后的误差依此为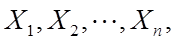 它们相互独立,都在[-0.5,0.5]上服从均匀分布。求
它们相互独立,都在[-0.5,0.5]上服从均匀分布。求
- 1200个数相加时,误差总和的绝对值小于10的概率。
- 多少个数相加时,误差总和的绝对值小于15的概率大于0.9。
定理5.5:(德莫佛-拉普拉斯积分极限定理)
设伯努利试验中,事件A发生的概率为p(0<p<1),m为n重伯努利试验中事件A发生的次数,则对任意的x,均有


应用:当n充分大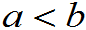 ,
, .
.
例:有一大批种子其中良种占20%,从中任取5000粒 ,试问这些种子中良种所占比例与
,试问这些种子中良种所占比例与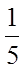 (即20%)之差小于0.01的概率。
(即20%)之差小于0.01的概率。
注 : * 可认为是有放回抽取。
* 可认为是有放回抽取。
例.设某车间有150台机床独立工作, 已知每台机床在运转时耗电量都是5(千瓦).因检修等原因,每台机床平均只有60%的时间在运转.试问,配电室至少要供给这个车间多少电.才能以99.9%的概率保证这个车间不致因供电不足而影响机床工作.
实用中: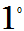
 较小,
较小,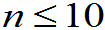 ,
,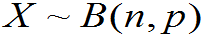 ;
;
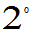
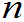 较大,
较大,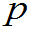 较小,
较小,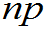 适中,
适中,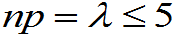 为好,
为好,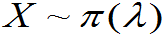 .
.
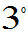
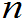 较大,
较大,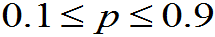 时,
时, .
.




