第四章 随机变量的数字特征3

§4.4 协方差及相关系数

一.协方差与相关系数的概念

1.定义

定义4.4：设二维随机变量(X,Y),它的分量的数学期望为E(X),E(Y)，若E[(X-E(X))(Y-E(Y))]存在，则称它为X,Y的协方差，记为Cov(X,Y),即

Cov(X,Y)=E[(X-E(X))(Y-E(Y))]

 

2.计算

(1)用定义计算

若二维离散型随机变量(X,Y)的联合概率分布律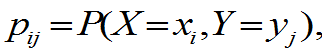i,j=1,2,¼，且Cov(X,Y)存在,则

Cov(X,Y)=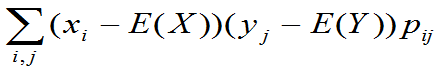

若二维连续型随机变量(X,Y)的联合概率密度为f(x,y),且Cov(X,Y)存在，则

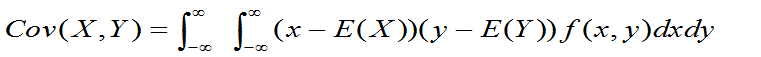
（2）、公式

在计算Cov(X,Y)时，除用定义外，有时用下述公式较方便：

Cov(X,Y)=E(XY)-E(X)E(Y)

第一版例：不讲。    

例 :设(X,Y)在圆域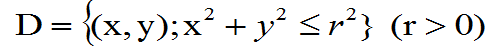上服从均匀分布，判断X,Y是否不相关。并求Cov(X,Y)。

例 :设(X,Y)的联合分布律为

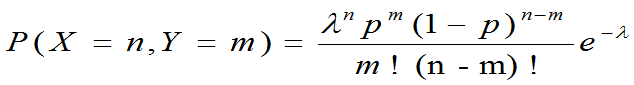
其中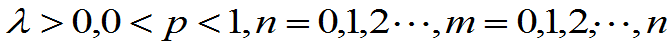

求 Cov(X,Y),并讨论X,Y的相关性。

说明：

(1)Cov(X,Y)能反映X与Y之间某种联系的程度。

(2)Cov(X,Y)是有量纲的量，其值与(X,Y)的取值单位有关。

3.相关系数

定义4.5:若二维随机变量(X,Y)的分量的方差D(X),D(Y)都存在，且D(X)>0,D(Y)>0,则称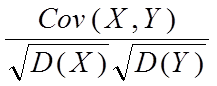为X,Y的相关系数，记为r_XY,即

r_XY=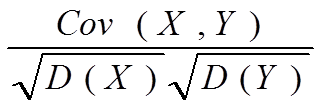

定义4.6：若r_XY=0则称X,Y不相关；

若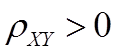称X,Y正相关；

若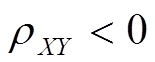则称X,Y负相关。

4.随机变量X,Y独立性与不相关的关系

(1)一般情况下，设存在，若X,Y相互独立,

则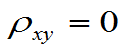，即X,Y不相关。

反之，X,Y不相关,但X,Y不一定独立。

如例 ：（书4.31）（X，Y）在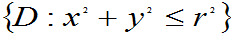上均匀分布。可知X，Y 不相关，但X，Y不独立。

(2)特别，对于二维正态分布(X,Y)服从

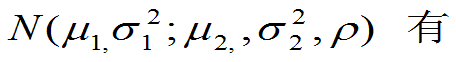
X,Y相互独立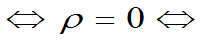 X,Y不相关。

二 协方差与相关系数的性质

1.性质

性质1:若X,Y的协方差Cov(X,Y)存在，则

E(XY)=E(X)E(Y)+Cov(X,Y)

性质2:若(X,Y)两个分量的方差都存在，则

D(X±Y)=D(X)+D(Y)±2Cov(X,Y)

推论:若(X₁,X_2,,...X_n)各分量的方差都存在，则

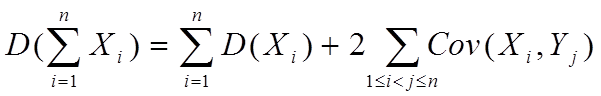
性质3:设下述各式所出现的协方差都存在，则有

Cov(X,Y)=Cov(Y,X)

Cov(aX,Y)=a Cov(X,Y)             

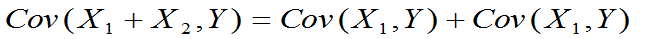
Cov(X,X)=D(X)

Cov(a,X)=0 其中a为常数

例3(第一版)：设（X，Y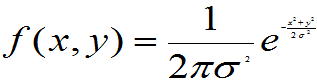）~，求

Cov(2X+Y,)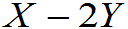

性质4:若 X,Y的相关系数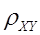存在，则

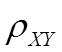(1)êï£1;

(2)½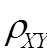ï=1的充要条件是：存在常数a,b 且a¹0,使得概率为1的有Y=aX+b, 即

P(Y=aX+b)=1    

证法一见书P-120.

几点说明:

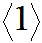
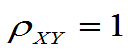
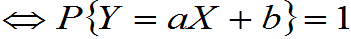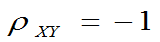
1. 由性质的证明可见：，a>0 ，这时称X与Y完全正相关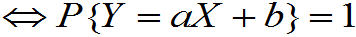；，a<0,这时称X与Y完全负相关。

完全正相关和完全负相关统称为完全相关，当X与Y完全相关时,(X,Y)可能取的值概率为1的集中在一条直线上。

(2)相关系数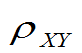是用来刻画X,Y 线性相关性程度的一个数量。当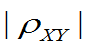越接近于1时，X与Y之间越近似有线性关系；当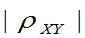较小时， X与Y之间不能认为有近似的线性关系。

1. 当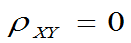时，X,Y不相关，X,Y之间没有线

性关系。这时,X,Y之间的关系较复杂；可能X,Y相互独立(如二维正态分布),可能(X,Y)在平面的某个区域内服从均匀分布(如例4.31)，可能X,Y之间有某种非线性的函数关系(如下面的例4.33)。

例1 P121

§4.5 矩、协方差矩阵

定义4.7:设二维随机变量(X,Y),k,l为非负整数。

若E(X^k)存在，则称它为X的k阶原点矩,简称k阶矩；

若E{[X-EX]^k}, k=1,2,….存在，则称它为X的k阶中心矩。

若E(X^kY^l)存在，则称它为X和Y的(k,l)阶混合矩，记作m _kl, 即m_kl=E(X^kY^l)；

若E[(X-E(X))^k(Y-E(Y))^l]存在，则称它为X和Y的(k,l)阶混合中心矩，记作s_kl, 即s_kl=E[(X-E(X))^k(Y-E(Y))^l]。

显然，数学期望E(X)是X的一阶矩，方差D(X)是X的二阶中心矩,协方差Cov(X,Y)是X和Y的(1,1)阶混合中心矩.

关于矩有下述结论：设k为正整数。

1. 若E(X^k)存在，则对小于k的一切非负整数

l，E(X^l)存在.这由½Xï£1+êXï^k，即得

EêXï^l£1+EêXï^k<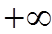

1. 原点矩与中心矩可相互表示。

协方差矩阵

P123—125.

略。

本章练习题

5,6,7,8,9,10,15(1),16,17,22,23,26,28.