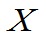第四章 随机变量的数字特征
讨论随机变量数字特征的原因
- 在实际问题中,有的随机变量的概率分布
难确定,有的不可能知道,而它的一些数字特征较易确定。
(2)实际应用中,人们更关心概率分布的数字特征。
(3)一些常用的重要分布,如二项分布、泊松
分布、指数分布、正态分布等,只要知道了它们的某些数字特征,就能完全确定其具体的分布。
§4.1 数学期望
一、数学期望的概念
1.离散性随机变量的数学期望
例4.1:大学一年级某班有32名同学,年龄情况如下:
年龄 | 17 | 18 | 19 | 20 | 21 | 22 |
人数 | 2 | 7 | 10 | 8 | 4 | 1 |
求该班同学的平均年龄。
解:
平均年龄=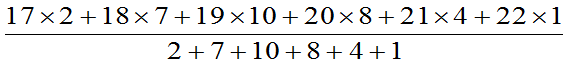
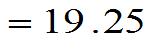
把上式改写为:
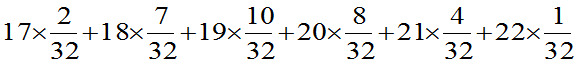
设X为从该班任选一名同学的年龄,其概率分布为
X | 17 | 18 | 19 | 20 | 21 | 22 |
P | 2/32 | 7/32 | 10/32 | 8/32 | 4/32 | 1/32 |
定义4.1:设离散型随机变量X的分布列为:
| x1 | x2 | x3 | …. | xk | …. |
| p1 | p2 | p3 | …. | Pk | …. |
若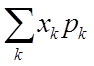 绝对收敛(即
绝对收敛(即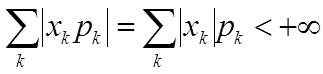 ),则称它为X的数学期望或均值(此时,也称X的数学期望存在),记为E(X),即
),则称它为X的数学期望或均值(此时,也称X的数学期望存在),记为E(X),即

若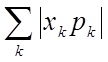 发散,则称X的数学期望不存在。
发散,则称X的数学期望不存在。
说明:
(1)随机变量的数学期望是一个实数,它体现了随机变量取值的平均;
- 要注意数学期望存在的条件:
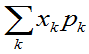 绝对
绝对
收敛;
- 当X服从某一分布时,也称某分布的数学
期望为EX 。
例4.2:设X服从参数为p的两点分布,求EX
EX=p
例4.3:设X~B(n,p),求EX
EX=np
例4.4:设X服从参数为l的泊松分布,求EX
EX=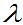
2.连续型随机变量的数学期望
定义4.2: 设连续型随机变量X 的概率密度为f(x).若积分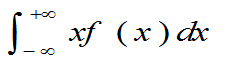
 绝对收敛,(即
绝对收敛,(即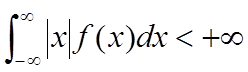 ),则称它为X的数学期望或均值(此时,也称X的数学期望存在),记为E(X),即
),则称它为X的数学期望或均值(此时,也称X的数学期望存在),记为E(X),即
 若
若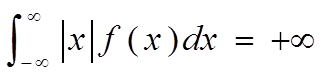 ,则称X的数学期望不存在。
,则称X的数学期望不存在。
例4.5:设X服从U[a,b],求E(X)。
EX=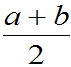
例4.6:设X服从参数为l的指数分布,求EX
EX=
例4.7: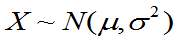 ,求EX
,求EX
EX=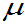
下面分析书上P101---P104例。
- P101
- P101
- P102---103
解:注意由于8:00~9:00, 9:00~10:00都恰有一辆车到站,所以(i)8:00到车站的旅客在8:50前一定会上车,而(ii)8:20到车站的旅客则可以直到9:50才会上车。
例4 P103
3.随机变量函数得数学期望
定理4.1:设随机变量X的函数为Y =g(X),
- 若离散型随机变量X的分布律为
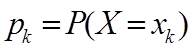 ,k =1,2,… ,
,k =1,2,… , 绝对收敛,则Y的数学期望存在,且
绝对收敛,则Y的数学期望存在,且 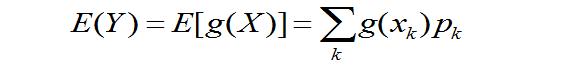
- 若连续型随机变量X的概率密度为
f(x), Y =g(X)也是连续型随机变量, 绝对收敛,则Y的数学期望存在,且
绝对收敛,则Y的数学期望存在,且

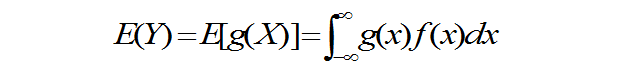
定理4.2:设二维随机变量(X ,Y )的函数Z=g(x,y)
- 若二维离散型随机变量(X,Y)的联合分布律
为
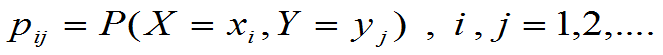
且有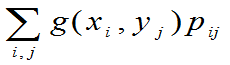 绝对收敛,则Z的数学期望存在,且
绝对收敛,则Z的数学期望存在,且
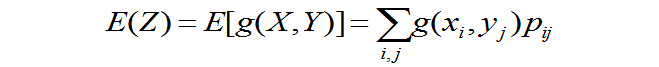
- 若二维连续型随机变量(X,Y)的联合概率密
度为 f (x,y),Z=g(X,Y) 也是连续型随机变量,并且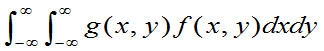 绝对收敛,则Z的数学期望存在,且
绝对收敛,则Z的数学期望存在,且

例5 P106
例6 P107
例7 P107
以下为第一版例。
例4.8:设X~U[0,p],Y=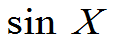 ,求E(Y )。
,求E(Y )。
例4.9:设(X,Y)的联合分布律为

其中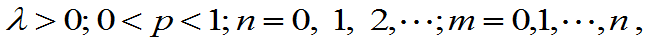
求E(XY)。
二.数学期望的性质
性质1:若c为常数,则
E(c)=c。
性质2:若c为常数,随机变量X 的数学期望存在,则:cX的数学期望存在,且E(cX)=cE(X)
性质3:若二维随机变量(X,Y)的分量X,Y的数学期望都存在,则X+Y的数学期望存在,且
E(X+Y)=E(X)+E(Y)
推论:若n维随机变量(X1,X2,...,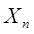 )的分量X1,X2,...,
)的分量X1,X2,...,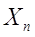 的数学期望都存在,则X1 + X2 +...+
的数学期望都存在,则X1 + X2 +...+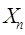 的数学期望存在,且
的数学期望存在,且

性质4:若随机变量X,Y相互独立,它们的数学期望都存在,则X·Y的数学期望存在,且
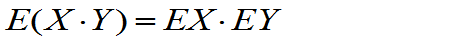
推论:若随机变量X1,X2,....,Xn相互独立,它们的数学期望都存在,则X1X2…Xn的数学期望存在,且

性质5:若随机变量只取非负值,又E(X)存在,则E(X)³0。

 若
若 对任何
对任何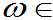
 ,
,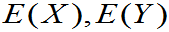 存在,则
存在,则

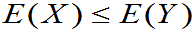 。
。
 特别地,若
特别地,若 为常数,
为常数,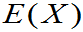 存在,则
存在,则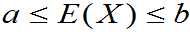 。
。
例8 P109
例9 P110
第一版例
例4.14:设一批同类型的产品共有N件,其中次品有M件。今从中任取n(假定n≤N-M)件,记这n件中所含次品数为X,求E(X)。
三.综合性的例题(第一版)
例:设X的概率密度为
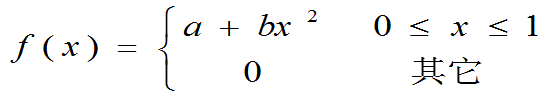 ,
,
其中a,b为常数,且E(X)= 。求a,b的值。
。求a,b的值。
注意:f(x)中有几个未知数要建几个方程来求之。
例: 射击比赛规定:每位射手向目标独立重复射击四法子弹,全未中的0分,仅中一发得15分,恰中两发得30分,恰中三发得55分,全中得100分。若某射手的命中率为0.6,求他得分的数学期望。
例:某水果商店,冬季每周购进一批苹果。已知该店一周苹果销售量X(单位:kg)服从U[1000,2000]。购进的苹果在一周内售出,1kg获纯利1.5元;一周内没售出,1kg需付耗损、储藏等费用0.3元。问一周应购进多少千克苹果,商店才能获得最大的平均利润。