§3.5 多维随机变量函数的分布
这一节是很重要的内容,一般概率统计的考试必有这些内容的考题。
特别是本节例1,3,4以及Max(X,Y),Min(X,Y)的分布等内容,很有代表性。
一.离散型随机变量(X,Y)的函数的概率分布
例1:已知(X,Y)的分布律为:
|
X Y |
-1 1 2 |
|
-1 2 |
5/20 2/20 6/20 3/20 3/20 1/20 |
求:Z1=X+Y,Z2 =max(X,Y)的分布律。
|
P |
5/20 |
2/20 |
6/20 |
3/20 |
3/20 |
1/20 |
|
(X,Y)取值 |
(-1,-1) |
(-1,1) |
(-1,2) |
(2,-1) |
(2,1) |
(2,2) |
|
Z1取值 |
-2 |
0 |
1 |
1 |
3 |
4 |
|
Z2取值 |
-1 |
1 |
2 |
2 |
2 |
2 |
二.连续型随机变量(X,Y)的函数的概率分布
-
已知(X,Y)~f(x,y),求Z=g(X,Y)的概率密度。
- Z~FZ(z)=P(Z£z)=P{g(X,Y)£z}=
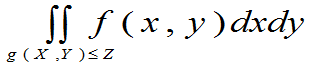 ,
, - Z~fZ(z)= F'Z(z)
- Z~FZ(z)=P(Z£z)=P{g(X,Y)£z}=
2.已知(X,Y)~f(x,y),求Z=X+Y的概率密度
定理3.4 若(X,Y)的联合概率密度为f(x,y),则Z=X+Y的概率密度为
fZ(z)=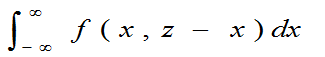
或 fZ(z)=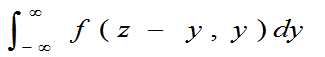 。
。
证明:P85---86.
讲P85.。。。
推论 若X,Y相互独立,它们的概率密度分别为fX(x)和fY(y),则独立和Z=X+Y的概率密度为
fZ(z)=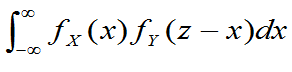 (3.36)
(3.36)
或 fZ(z)=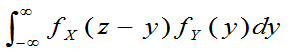 (3.37)
(3.37)
例1 P86 设X和Y是两个相互独立的随机变量,它们都服从N(0,1),即。。
求Z=X+Y的概率密度。
一般,设X,Y相互独立且 ,
,
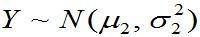 ,则Z=X+Y仍然服从正态分布,且有
,则Z=X+Y仍然服从正态分布,且有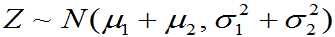 。此结论可以推广到n个独立正态随机变量之和的情况。即若
。此结论可以推广到n个独立正态随机变量之和的情况。即若
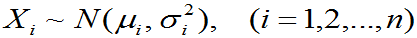 ,且它们相互独立,则它们的和
,且它们相互独立,则它们的和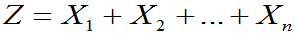 仍然服从正态分布,且有
仍然服从正态分布,且有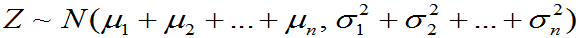
更一般地,可以证明有限个相互独立的正态随机变量的线性组合仍然服从正态分布。
例2 P87
例3 P88
例3结论的推广,n个相互独立的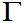 分布变量之和仍服从
分布变量之和仍服从 分布。
分布。
例(第一版):设R.V. X与Y相互独立,X~f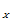 (x)=
(x)= , Y~f
, Y~f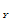 (y)=
(y)=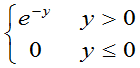 , 求 Z=X+Y的分布密度函数。
, 求 Z=X+Y的分布密度函数。
例:(书上例3.17) 已知X,Y相互独立,均服从N(0,1),求Z=X+Y的概率密度。
例(第一版):(书上例3.18) 设X,Y相互独立,它们的概率密度分别为fX(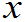 )=
)=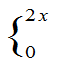
 ,fY(y)=
,fY(y)=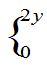
 ,求Z=X+Y的概率密度。
,求Z=X+Y的概率密度。
3.M=max(X,Y),N=min(X,Y)的概率分布
定理3.6 若X,Y相互独立,它们的分布函数分别为FX(x),FY(y),则
-
M=max(X,Y)的分布函数为:FM(z)=FX(z)·FY(z)
-
N=min(X,Y)的分布函数为:
FN(z)=1-(1- FX(z))·(1-FY(z))
这里的结论很重要。
可以推广到更一般的情形。如。。。。
定理3.7 已知X1、X2、…、Xn相互独立。
-
若j1(X1)、j2(X2)、…、 jn(Xn)分别是X1、X2、…、Xn的函数,则j1、j2、…、 jn相互独立。
-
若j是X1、X2、…、Xn中某k个随机变量Xi1、Xi2、…、Xik的函数,y是另外m个随机变量Xj1、Xj2、…、Xjl的函数,则j,y相互独立。




