§3.3 条件分布
由条件概率引出条件概率分布的概念。
定义1 设(X,Y)是二维离散型随机变量,对于固定的 ,若
,若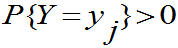 ,则称
,则称
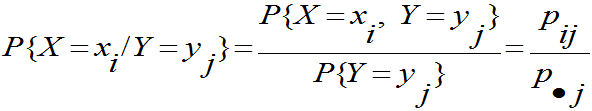
例1, P77,一射手进行射击,击中目标的概率为p(0<p<1),射击到击中目标两次为止。设以X表示首次击中目标所进行的射击次数,以Y表示总共进行的射击次数,试求X和Y的联合分布律及条件分布律。
解:
定义2 (不严格),设(X,Y)的概率密度为
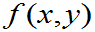 ,记
,记 为在条件Y=y下X的条件概率密度,则
为在条件Y=y下X的条件概率密度,则
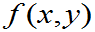
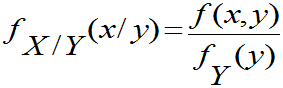
P79 求条件边缘分布和密度公式的推导过程。
公式3.4和3.5.
- P79,
例3 P80,
§3.4 随机变量的独立性
1.概念:
定义3.5 设(X,Y)的联合分布函数为F(x,y),X,Y的边缘分布函数分别为FX(x), FY(y)。
若对任意的实数x,y,均有 F(x,y)=FX(x)·FY(y) (3.30)
即 P{X£x,Y£y}=P{X£x}·P{Y£y}
则称X,Y相互独立。
- 电子仪器由两个部件构成,以X和Y分别表示两个部件的寿命(单位千小时)。已知X和Y的联合分布函数为:
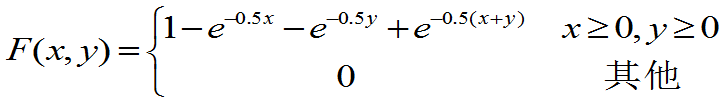 ,
,
- 问X与Y是否独立?
解:独立。
因为:

2.判断两个随机变量是否独立的定理
定理3.1 二维随机变量(X,Y)的两个分量X,Y相互独立的充要条件是:对任意的实数x1<x2,y1<y2,均有
P{x1<X£x2,y1<Y£y2}=P{x1<X£X2}· P{ y1<Y£y2}。
定理3.1' 二维随机变量(X,Y)的两个分量X,Y相互独立的充要条件是:对任意的实数x,y,均有
P{X>x,Y>y}=P{X>x}P{Y>y}
定理3.2 设二维离散型随机变量(X,Y)的联合分布律,边缘分布律分别为pij, pi. ,p.j, i,j=1,2,…,则 X,Y相互独立的充要条件是:对任意的i,j均有
pij=pi.p.j
即 P{X=xi,Y=yj}=P{X=xi}·P{Y=yj}
定理3.3 设连续型随机变量X,Y的概率密度分别为fX(x) ,fY(y),则X,Y相互独立的充要条件是: fX(x)fY(y)=f(x,y)
其中:f(x,y)是(X,Y)的联合概率密度。
例6:(续例3.5第一版 )第二版P82,这里的结论很重要。
设 (X,Y)服从于N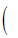
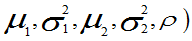 ,证明 X,Y相互独立的充要条件是:
,证明 X,Y相互独立的充要条件是: =0。
=0。
证明:由第一版例3.5知(X,Y)的联合概率密度、X和Y的边缘概率密度分别为
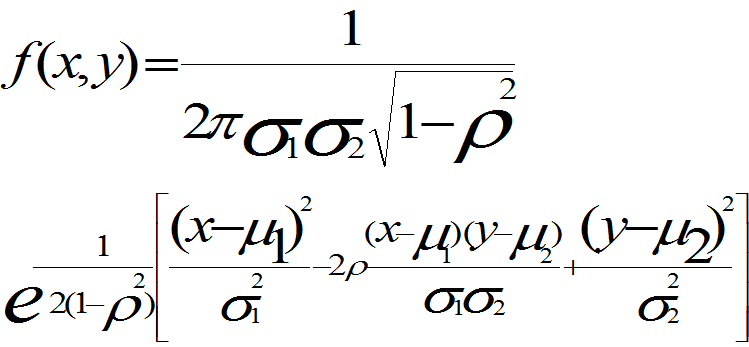
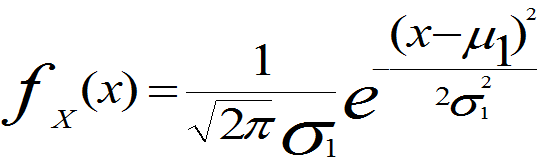
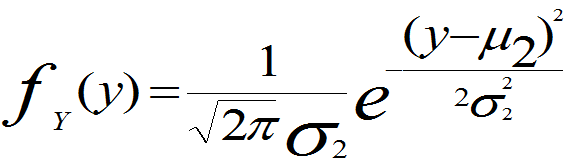
充分性 若r=0,此时二元函数
fX(x)fY(y)=f(x,y)
是(X,Y)的联合概率密度,所以X,Y相互独立;
必要性 若X,Y相互独立,则
f(x,y)=fX(x)fY(y)
取x=m1、y=m2代入上式,即得
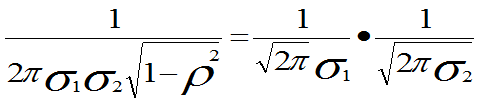
于是r=0。
例1 P83,挺怪一例子,好象是为了算概率而不是为了说明这段的内容。
3.二维随机变量独立性概念的推广
定义3.6 设(X1、X2、…、Xn)是n维随机变量,其联合分布函数和一维边缘分布函数分别为F(x1、x2、…、,xn)、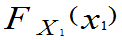 、
、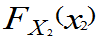 、…、
、…、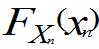
 ,若对任意的实数x1、x2、…、xn均有
,若对任意的实数x1、x2、…、xn均有
F(x1、x2、…、,xn)=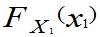 ·
·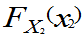 …
…
则称X1、X2、…、Xn相互独立。
定义3.7 设X1、X2、…、Xn、…是一列随机变量,若其中任意有限个随机变量是相互独立的,则称这一列随机变量是相互独立的。




