第三章 多维随机变量及其分布3

3．边缘概率密度

设二维连续型随机变量(X,Y) 联合分布函数、联合概率密度分别为F(x,y),f(x,y),分量X,Y的边缘分布函数分别为F_X(x)、F_Y(y)。利用边缘分布函数与联合分布函数的关系及(3.16)式，可得

F_X(x)=F(x,+¥)=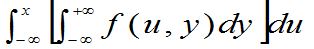 (3.17)

F_Y(y)=F(+¥,y)= 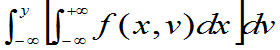(3.18)

 

记：f_X(x)=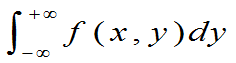 为X的边缘概率密度函数；f_Y(y)= 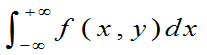为Y的边缘概率密度函数。

 

例2： P74

 

例3： P75 即下面的例5（第一版）,若二维随机变量(X,Y)的联合概率密度为

 

f(x,y)=

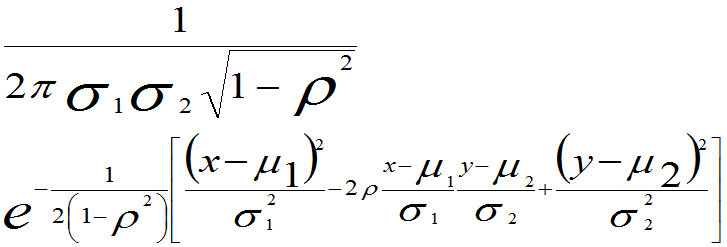
其中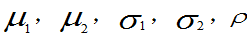均为常数，且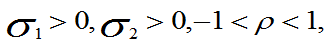则称(X,Y)服从参数为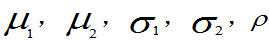的二维正态分布,通常记为 (X,Y)服从于N。

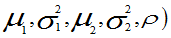求：(X,Y)的边缘概率密度 f_X(x) ,f_Y(y)。

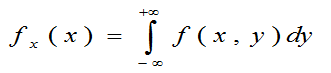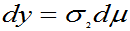解：令：且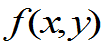中e的指数部分改写为：

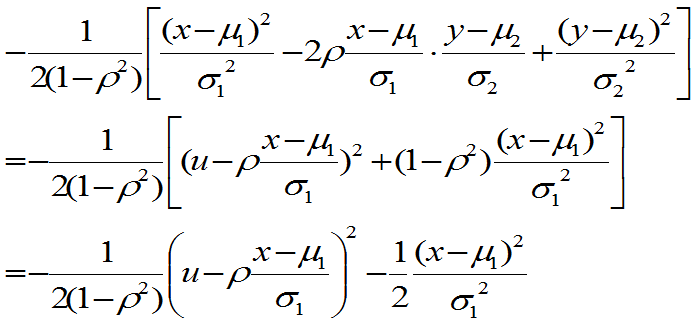
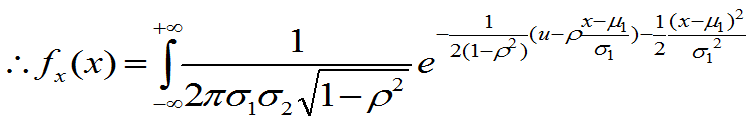
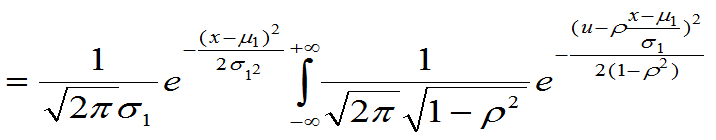
是的积分函数，    积分=1。

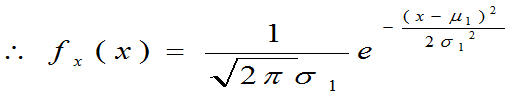即知：X服从于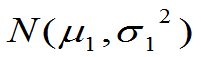，同理：Y服从于

结果表明：

（1）二维正态分布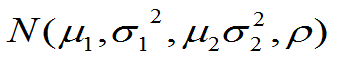，其边缘分布都是一维正态分布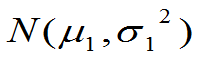和 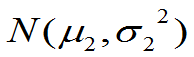。而反之不然。

 

（2）二维R.V.边缘分布是由联合分布唯一确定。

 

（见第一版习题3.1）

 

 

 

 

例4： （第一版 书上例3.4） 设(X,Y)在圆域D={(x,y): x²+y²£ r²}(r > 0)上服从均匀分布，其联合概率密度为

f(x,y)=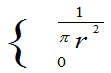

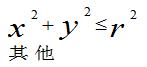
求(1)P{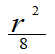<X²+Y²£};

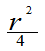(2)(X,Y)的边缘概率密度函数f_X(x) ,f_Y(y)。